Synthesizing and Adapting Error Correction Data for Mobile Large Language Model Applications

Error correction is an important capability when applying large language models (LLMs) to facilitate user typing on mobile devices. In this paper, we use LLMs to synthesize a high-quality dataset of error correction pairs to evaluate and improve LLMs for mobile applications. We first prompt LLMs with error correction domain knowledge to build a scalable and reliable addition to the existing data synthesis pipeline. We then adapt the synthetic data distribution to match the mobile application domain by reweighting the samples. The reweighting model is learnt by predicting (a handful of) live A/B test metrics when deploying LLMs in production, given the LLM performance on offline evaluation data and scores from a small privacy-preserving on-device language model. Finally, we present best practices for mixing our synthetic data with other data sources to improve model performance on error correction in both offline evaluation and production live A/B testing.

Who You Are Matters: Bridging Topics and Social Roles via LLM-Enhanced Logical Recommendation

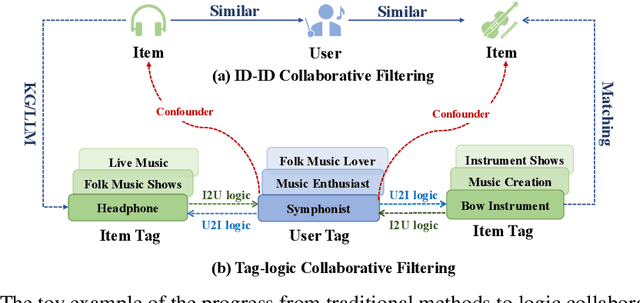
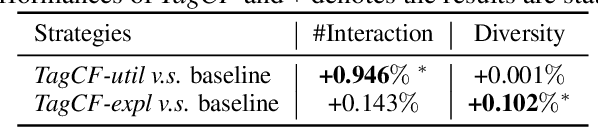
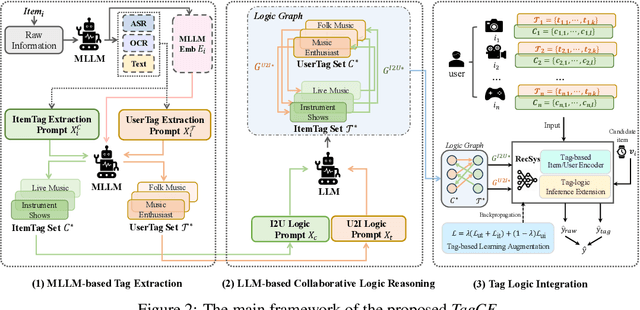
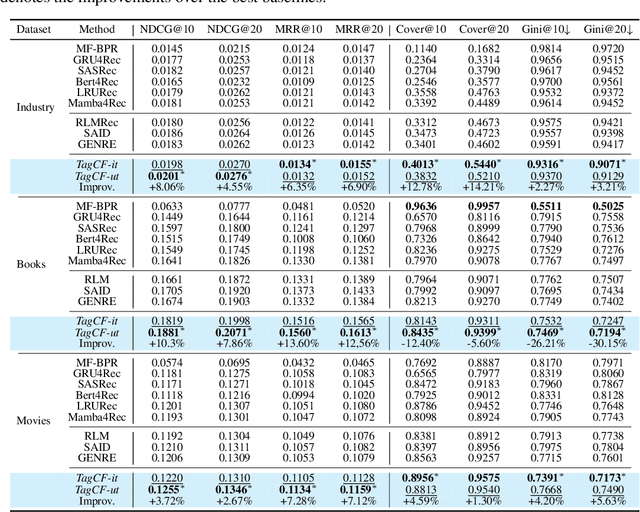
Recommender systems filter contents/items valuable to users by inferring preferences from user features and historical behaviors. Mainstream approaches follow the learning-to-rank paradigm, which focus on discovering and modeling item topics (e.g., categories), and capturing user preferences on these topics based on historical interactions. However, this paradigm often neglects the modeling of user characteristics and their social roles, which are logical confounders influencing the correlated interest and user preference transition. To bridge this gap, we introduce the user role identification task and the behavioral logic modeling task that aim to explicitly model user roles and learn the logical relations between item topics and user social roles. We show that it is possible to explicitly solve these tasks through an efficient integration framework of Large Language Model (LLM) and recommendation systems, for which we propose TagCF. On the one hand, the exploitation of the LLM's world knowledge and logic inference ability produces a virtual logic graph that reveals dynamic and expressive knowledge of users, augmenting the recommendation performance. On the other hand, the user role aligns the user behavioral logic with the observed user feedback, refining our understanding of user behaviors. Additionally, we also show that the extracted user-item logic graph is empirically a general knowledge that can benefit a wide range of recommendation tasks, and conduct experiments on industrial and several public datasets as verification.

Explicit Uncertainty Modeling for Video Watch Time Prediction

In video recommendation, a critical component that determines the system's recommendation accuracy is the watch-time prediction module, since how long a user watches a video directly reflects personalized preferences. One of the key challenges of this problem is the user's stochastic watch-time behavior. To improve the prediction accuracy for such an uncertain behavior, existing approaches show that one can either reduce the noise through duration bias modeling or formulate a distribution modeling task to capture the uncertainty. However, the uncontrolled uncertainty is not always equally distributed across users and videos, inducing a balancing paradox between the model accuracy and the ability to capture out-of-distribution samples. In practice, we find that the uncertainty of the watch-time prediction model also provides key information about user behavior, which, in turn, could benefit the prediction task itself. Following this notion, we derive an explicit uncertainty modeling strategy for the prediction model and propose an adversarial optimization framework that can better exploit the user watch-time behavior. This framework has been deployed online on an industrial video sharing platform that serves hundreds of millions of daily active users, which obtains a significant increase in users' video watch time by 0.31% through the online A/B test. Furthermore, extended offline experiments on two public datasets verify the effectiveness of the proposed framework across various watch-time prediction backbones.

Synthesizing Privacy-Preserving Text Data via Finetuning without Finetuning Billion-Scale LLMs

Synthetic data offers a promising path to train models while preserving data privacy. Differentially private (DP) finetuning of large language models (LLMs) as data generator is effective, but is impractical when computation resources are limited. Meanwhile, prompt-based methods such as private evolution, depend heavily on the manual prompts, and ineffectively use private information in their iterative data selection process. To overcome these limitations, we propose CTCL (Data Synthesis with ConTrollability and CLustering), a novel framework for generating privacy-preserving synthetic data without extensive prompt engineering or billion-scale LLM finetuning. CTCL pretrains a lightweight 140M conditional generator and a clustering-based topic model on large-scale public data. To further adapt to the private domain, the generator is DP finetuned on private data for fine-grained textual information, while the topic model extracts a DP histogram representing distributional information. The DP generator then samples according to the DP histogram to synthesize a desired number of data examples. Evaluation across five diverse domains demonstrates the effectiveness of our framework, particularly in the strong privacy regime. Systematic ablation validates the design of each framework component and highlights the scalability of our approach.

Prompt Public Large Language Models to Synthesize Data for Private On-device Applications

Pre-training on public data is an effective method to improve the performance for federated learning (FL) with differential privacy (DP). This paper investigates how large language models (LLMs) trained on public data can improve the quality of pre-training data for the on-device language models trained with DP and FL. We carefully design LLM prompts to filter and transform existing public data, and generate new data to resemble the real user data distribution. The model pre-trained on our synthetic dataset achieves relative improvement of 19.0% and 22.8% in next word prediction accuracy compared to the baseline model pre-trained on a standard public dataset, when evaluated over the real user data in Gboard (Google Keyboard, a production mobile keyboard application). Furthermore, our method achieves evaluation accuracy better than or comparable to the baseline during the DP FL fine-tuning over millions of mobile devices, and our final model outperforms the baseline in production A/B testing. Our experiments demonstrate the strengths of LLMs in synthesizing data close to the private distribution even without accessing the private data, and also suggest future research directions to further reduce the distribution gap.

Profit: Benchmarking Personalization and Robustness Trade-off in Federated Prompt Tuning

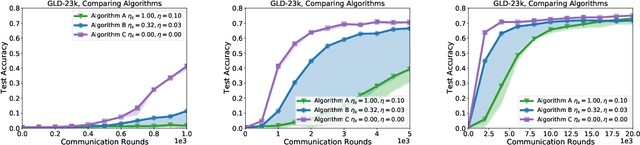
In many applications of federated learning (FL), clients desire models that are personalized using their local data, yet are also robust in the sense that they retain general global knowledge. However, the presence of data heterogeneity across clients induces a fundamental trade-off between personalization (i.e., adaptation to a local distribution) and robustness (i.e., not forgetting previously learned general knowledge). It is critical to understand how to navigate this personalization vs robustness trade-off when designing federated systems, which are increasingly moving towards a paradigm of fine-tuning large foundation models. Due to limited computational and communication capabilities in most federated settings, this foundation model fine-tuning must be done using parameter-efficient fine-tuning (PEFT) approaches. While some recent work has studied federated approaches to PEFT, the personalization vs robustness trade-off of federated PEFT has been largely unexplored. In this work, we take a step towards bridging this gap by benchmarking fundamental FL algorithms -- FedAvg and FedSGD plus personalization (via client local fine-tuning) -- applied to one of the most ubiquitous PEFT approaches to large language models (LLMs) -- prompt tuning -- in a multitude of hyperparameter settings under varying levels of data heterogeneity. Our results show that federated-trained prompts can be surprisingly robust when using a small learning rate with many local epochs for personalization, especially when using an adaptive optimizer as the client optimizer during federated training. We also demonstrate that simple approaches such as adding regularization and interpolating two prompts are effective in improving the personalization vs robustness trade-off in computation-limited settings with few local updates allowed for personalization.

Motley: Benchmarking Heterogeneity and Personalization in Federated Learning

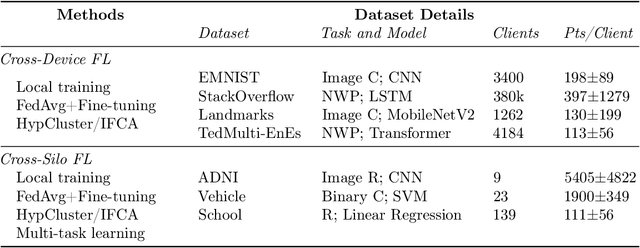
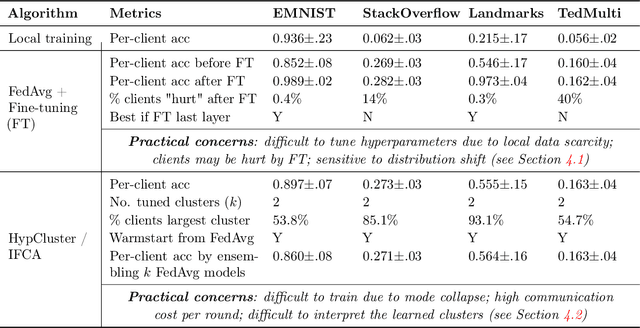
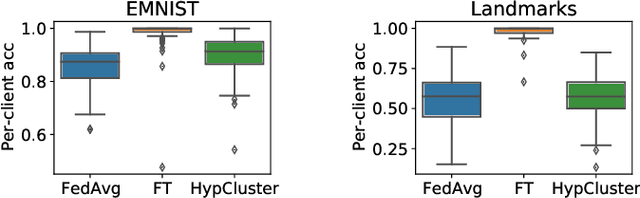
Personalized federated learning considers learning models unique to each client in a heterogeneous network. The resulting client-specific models have been purported to improve metrics such as accuracy, fairness, and robustness in federated networks. However, despite a plethora of work in this area, it remains unclear: (1) which personalization techniques are most effective in various settings, and (2) how important personalization truly is for realistic federated applications. To better answer these questions, we propose Motley, a benchmark for personalized federated learning. Motley consists of a suite of cross-device and cross-silo federated datasets from varied problem domains, as well as thorough evaluation metrics for better understanding the possible impacts of personalization. We establish baselines on the benchmark by comparing a number of representative personalized federated learning methods. These initial results highlight strengths and weaknesses of existing approaches, and raise several open questions for the community. Motley aims to provide a reproducible means with which to advance developments in personalized and heterogeneity-aware federated learning, as well as the related areas of transfer learning, meta-learning, and multi-task learning.

A Field Guide to Federated Optimization

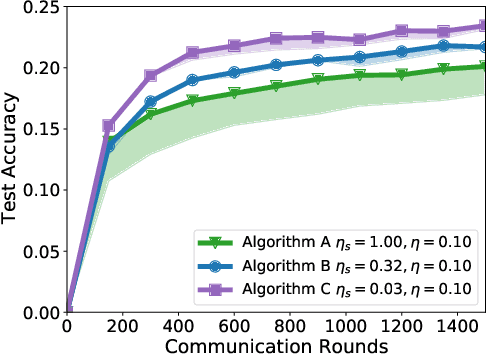
Federated learning and analytics are a distributed approach for collaboratively learning models (or statistics) from decentralized data, motivated by and designed for privacy protection. The distributed learning process can be formulated as solving federated optimization problems, which emphasize communication efficiency, data heterogeneity, compatibility with privacy and system requirements, and other constraints that are not primary considerations in other problem settings. This paper provides recommendations and guidelines on formulating, designing, evaluating and analyzing federated optimization algorithms through concrete examples and practical implementation, with a focus on conducting effective simulations to infer real-world performance. The goal of this work is not to survey the current literature, but to inspire researchers and practitioners to design federated learning algorithms that can be used in various practical applications.

Federated Reconstruction: Partially Local Federated Learning

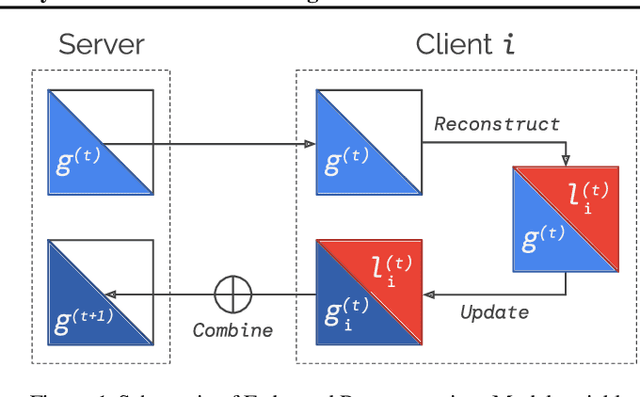
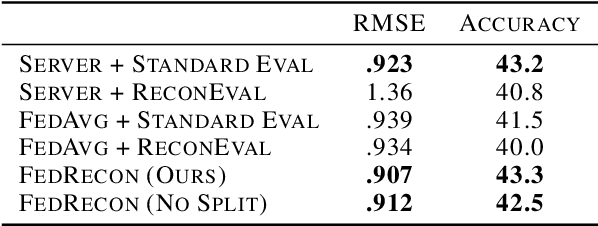
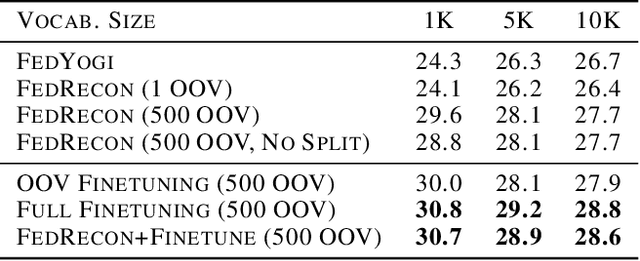
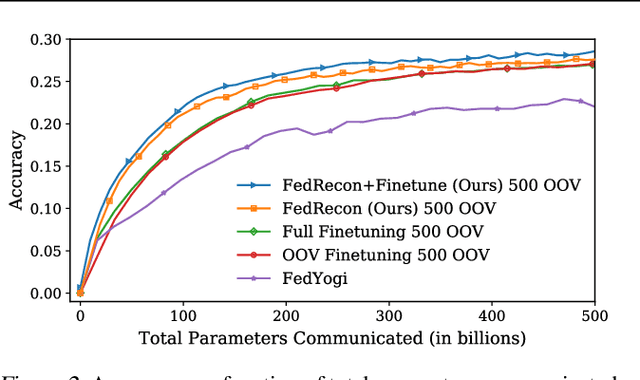
Personalization methods in federated learning aim to balance the benefits of federated and local training for data availability, communication cost, and robustness to client heterogeneity. Approaches that require clients to communicate all model parameters can be undesirable due to privacy and communication constraints. Other approaches require always-available or stateful clients, impractical in large-scale cross-device settings. We introduce Federated Reconstruction, the first model-agnostic framework for partially local federated learning suitable for training and inference at scale. We motivate the framework via a connection to model-agnostic meta learning, empirically demonstrate its performance over existing approaches for collaborative filtering and next word prediction, and release an open-source library for evaluating approaches in this setting. We also describe the successful deployment of this approach at scale for federated collaborative filtering in a mobile keyboard application.

Implicit Regularization of Normalization Methods

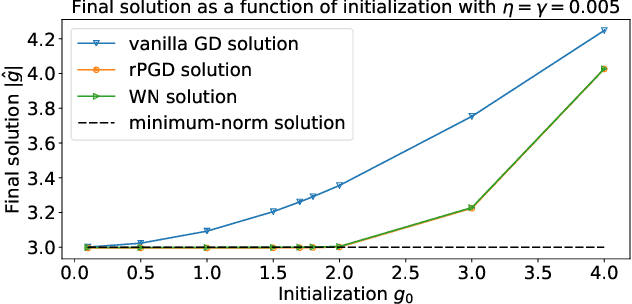
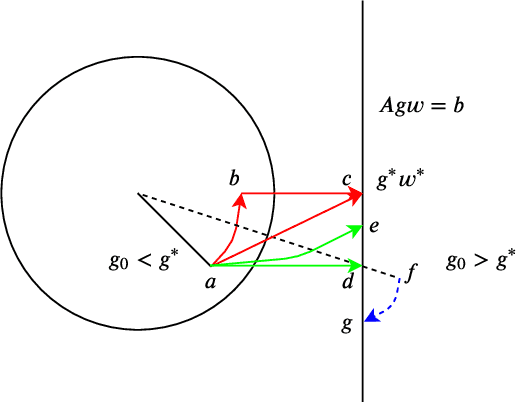
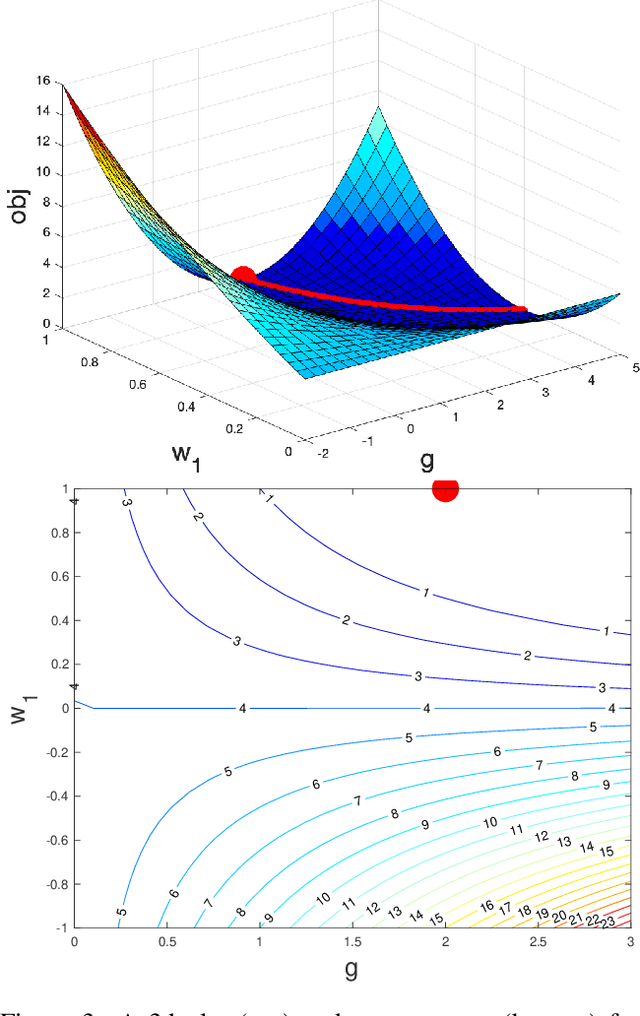
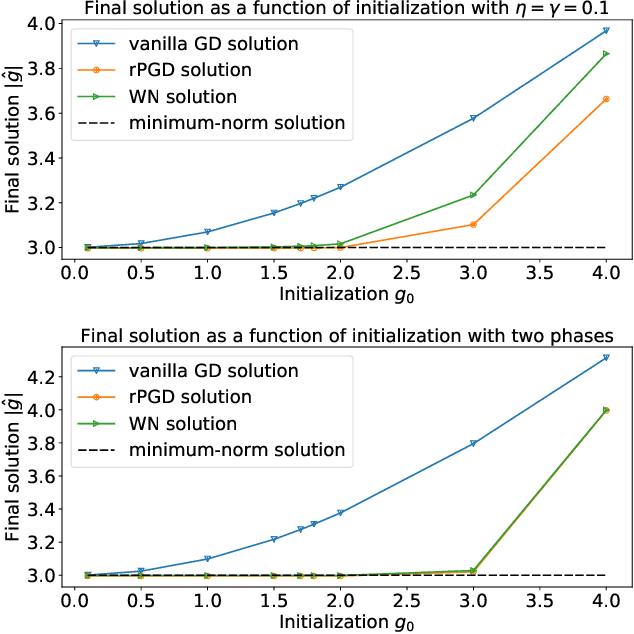
Normalization methods such as batch normalization are commonly used in overparametrized models like neural networks. Here, we study the weight normalization (WN) method (Salimans & Kingma, 2016) and a variant called reparametrized projected gradient descent (rPGD) for overparametrized least squares regression and some more general loss functions. WN and rPGD reparametrize the weights with a scale $g$ and a unit vector such that the objective function becomes \emph{non-convex}. We show that this non-convex formulation has beneficial regularization effects compared to gradient descent on the original objective. We show that these methods adaptively regularize the weights and \emph{converge with exponential rate} to the minimum $\ell_2$ norm solution (or close to it) even for initializations \emph{far from zero}. This is different from the behavior of gradient descent, which only converges to the min norm solution when started at zero, and is more sensitive to initialization. Some of our proof techniques are different from many related works; for instance we find explicit invariants along the gradient flow paths. We verify our results experimentally and suggest that there may be a similar phenomenon for nonlinear problems such as matrix sensing.