Implicit Regularization of Normalization Methods
Paper and Code
Nov 23, 2019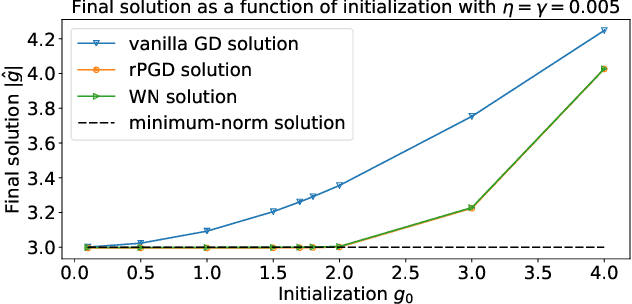
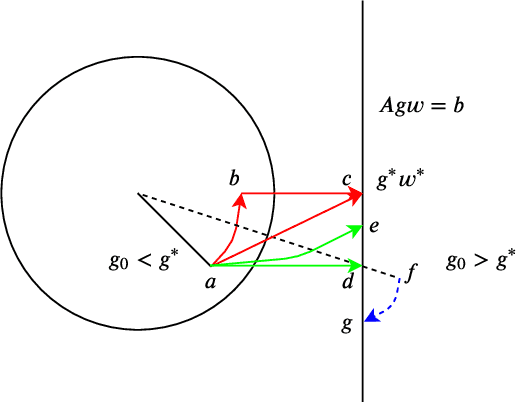
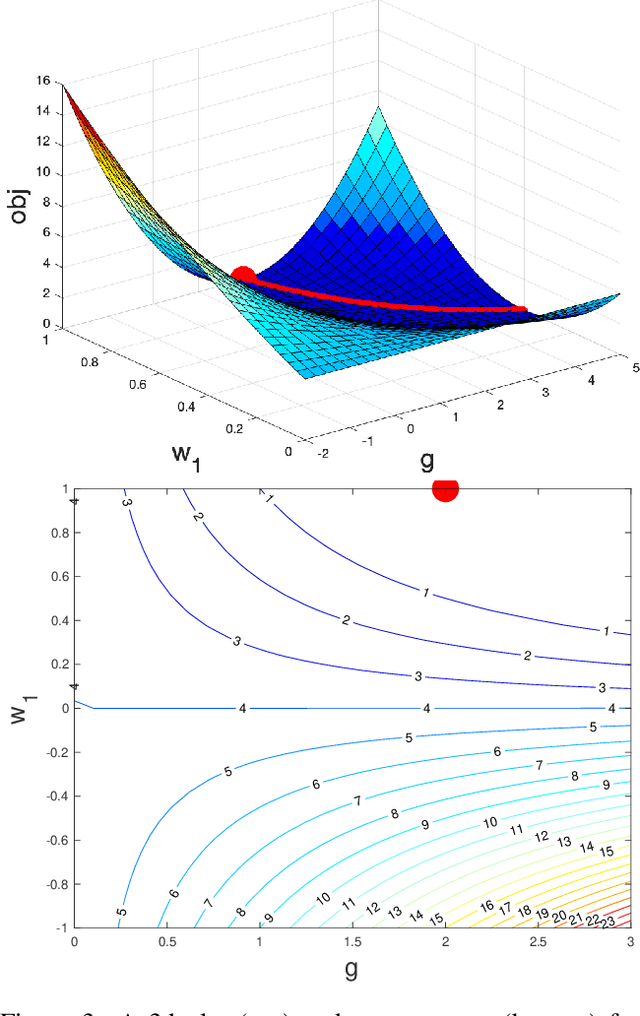
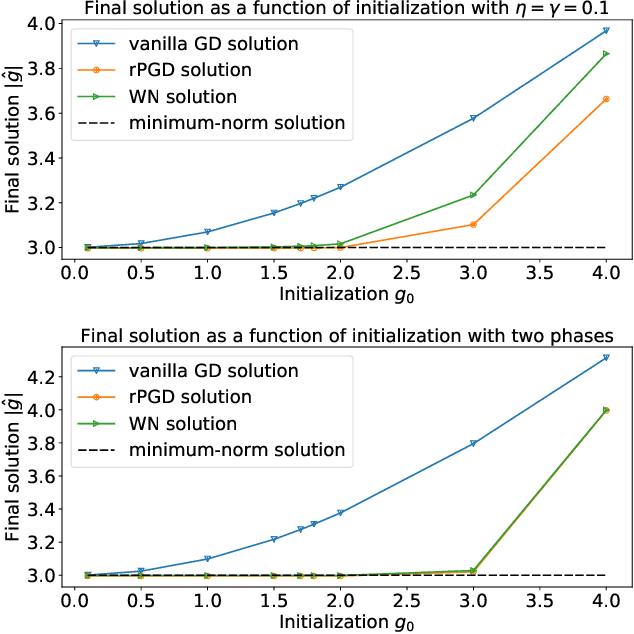
Normalization methods such as batch normalization are commonly used in overparametrized models like neural networks. Here, we study the weight normalization (WN) method (Salimans & Kingma, 2016) and a variant called reparametrized projected gradient descent (rPGD) for overparametrized least squares regression and some more general loss functions. WN and rPGD reparametrize the weights with a scale $g$ and a unit vector such that the objective function becomes \emph{non-convex}. We show that this non-convex formulation has beneficial regularization effects compared to gradient descent on the original objective. We show that these methods adaptively regularize the weights and \emph{converge with exponential rate} to the minimum $\ell_2$ norm solution (or close to it) even for initializations \emph{far from zero}. This is different from the behavior of gradient descent, which only converges to the min norm solution when started at zero, and is more sensitive to initialization. Some of our proof techniques are different from many related works; for instance we find explicit invariants along the gradient flow paths. We verify our results experimentally and suggest that there may be a similar phenomenon for nonlinear problems such as matrix sensing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge