Caption Anything in Video: Fine-grained Object-centric Captioning via Spatiotemporal Multimodal Prompting

We present CAT-V (Caption AnyThing in Video), a training-free framework for fine-grained object-centric video captioning that enables detailed descriptions of user-selected objects through time. CAT-V integrates three key components: a Segmenter based on SAMURAI for precise object segmentation across frames, a Temporal Analyzer powered by TRACE-Uni for accurate event boundary detection and temporal analysis, and a Captioner using InternVL-2.5 for generating detailed object-centric descriptions. Through spatiotemporal visual prompts and chain-of-thought reasoning, our framework generates detailed, temporally-aware descriptions of objects' attributes, actions, statuses, interactions, and environmental contexts without requiring additional training data. CAT-V supports flexible user interactions through various visual prompts (points, bounding boxes, and irregular regions) and maintains temporal sensitivity by tracking object states and interactions across different time segments. Our approach addresses limitations of existing video captioning methods, which either produce overly abstract descriptions or lack object-level precision, enabling fine-grained, object-specific descriptions while maintaining temporal coherence and spatial accuracy. The GitHub repository for this project is available at https://github.com/yunlong10/CAT-V

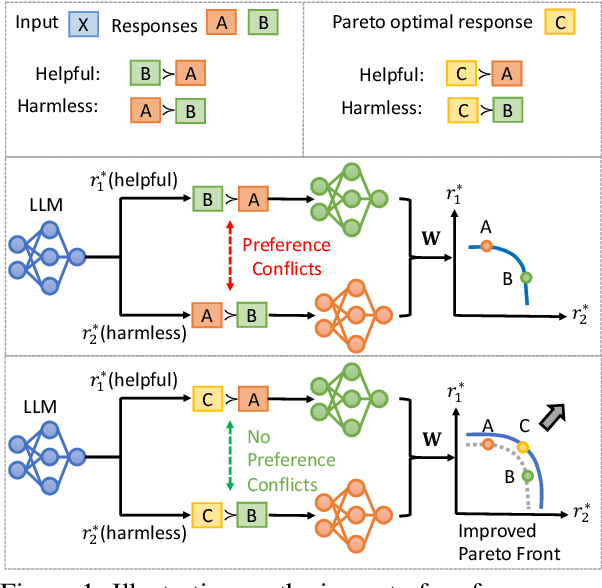
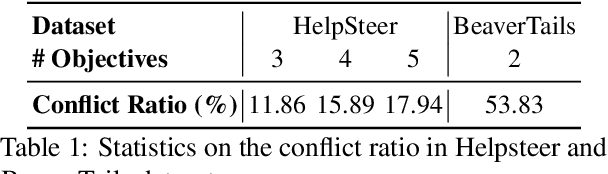
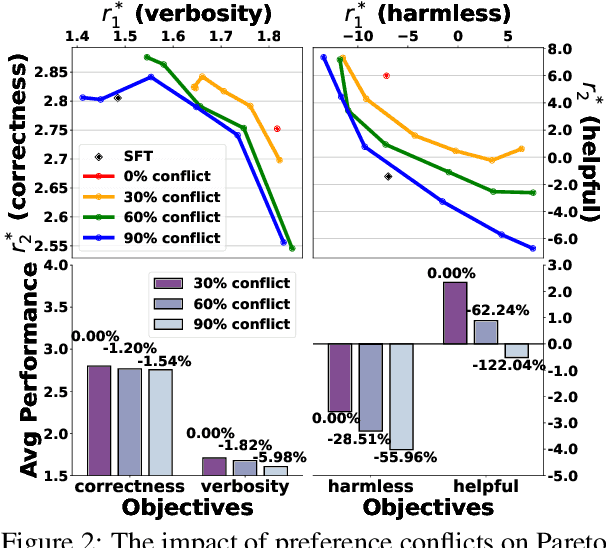
Self-Improvement Towards Pareto Optimality: Mitigating Preference Conflicts in Multi-Objective Alignment

Multi-Objective Alignment (MOA) aims to align LLMs' responses with multiple human preference objectives, with Direct Preference Optimization (DPO) emerging as a prominent approach. However, we find that DPO-based MOA approaches suffer from widespread preference conflicts in the data, where different objectives favor different responses. This results in conflicting optimization directions, hindering the optimization on the Pareto Front. To address this, we propose to construct Pareto-optimal responses to resolve preference conflicts. To efficiently obtain and utilize such responses, we propose a self-improving DPO framework that enables LLMs to self-generate and select Pareto-optimal responses for self-supervised preference alignment. Extensive experiments on two datasets demonstrate the superior Pareto Front achieved by our framework compared to various baselines. Code is available at \url{https://github.com/zyttt-coder/SIPO}.

Mitigating Hallucinations in Multimodal Spatial Relations through Constraint-Aware Prompting

Spatial relation hallucinations pose a persistent challenge in large vision-language models (LVLMs), leading to generate incorrect predictions about object positions and spatial configurations within an image. To address this issue, we propose a constraint-aware prompting framework designed to reduce spatial relation hallucinations. Specifically, we introduce two types of constraints: (1) bidirectional constraint, which ensures consistency in pairwise object relations, and (2) transitivity constraint, which enforces relational dependence across multiple objects. By incorporating these constraints, LVLMs can produce more spatially coherent and consistent outputs. We evaluate our method on three widely-used spatial relation datasets, demonstrating performance improvements over existing approaches. Additionally, a systematic analysis of various bidirectional relation analysis choices and transitivity reference selections highlights greater possibilities of our methods in incorporating constraints to mitigate spatial relation hallucinations.

Same Company, Same Signal: The Role of Identity in Earnings Call Transcripts

Post-earnings volatility prediction is critical for investors, with previous works often leveraging earnings call transcripts under the assumption that their rich semantics contribute significantly. To further investigate how transcripts impact volatility, we introduce DEC, a dataset featuring accurate volatility calculations enabled by the previously overlooked beforeAfterMarket attribute and dense ticker coverage. Unlike established benchmarks, where each ticker has only around two earnings, DEC provides 20 earnings records per ticker. Using DEC, we reveal that post-earnings volatility undergoes significant shifts, with each ticker displaying a distinct volatility distribution. To leverage historical post-earnings volatility and capture ticker-specific patterns, we propose two training-free baselines: Post-earnings Volatility (PEV) and Same-ticker Post-earnings Volatility (STPEV). These baselines surpass all transcripts-based models on DEC as well as on established benchmarks. Additionally, we demonstrate that current transcript representations predominantly capture ticker identity rather than offering financially meaningful insights specific to each earnings. This is evidenced by two key observations: earnings representations from the same ticker exhibit significantly higher similarity compared to those from different tickers, and predictions from transcript-based models show strong correlations with prior post-earnings volatility.

What Are Step-Level Reward Models Rewarding? Counterintuitive Findings from MCTS-Boosted Mathematical Reasoning

Step-level reward models (SRMs) can significantly enhance mathematical reasoning performance through process supervision or step-level preference alignment based on reinforcement learning. The performance of SRMs is pivotal, as they serve as critical guidelines, ensuring that each step in the reasoning process is aligned with desired outcomes. Recently, AlphaZero-like methods, where Monte Carlo Tree Search (MCTS) is employed for automatic step-level preference annotation, have proven particularly effective. However, the precise mechanisms behind the success of SRMs remain largely unexplored. To address this gap, this study delves into the counterintuitive aspects of SRMs, particularly focusing on MCTS-based approaches. Our findings reveal that the removal of natural language descriptions of thought processes has minimal impact on the efficacy of SRMs. Furthermore, we demonstrate that SRMs are adept at assessing the complex logical coherence present in mathematical language while having difficulty in natural language. These insights provide a nuanced understanding of the core elements that drive effective step-level reward modeling in mathematical reasoning. By shedding light on these mechanisms, this study offers valuable guidance for developing more efficient and streamlined SRMs, which can be achieved by focusing on the crucial parts of mathematical reasoning.

On the Role of Model Prior in Real-World Inductive Reasoning

Large Language Models (LLMs) show impressive inductive reasoning capabilities, enabling them to generate hypotheses that could generalize effectively to new instances when guided by in-context demonstrations. However, in real-world applications, LLMs' hypothesis generation is not solely determined by these demonstrations but is significantly shaped by task-specific model priors. Despite their critical influence, the distinct contributions of model priors versus demonstrations to hypothesis generation have been underexplored. This study bridges this gap by systematically evaluating three inductive reasoning strategies across five real-world tasks with three LLMs. Our empirical findings reveal that, hypothesis generation is primarily driven by the model's inherent priors; removing demonstrations results in minimal loss of hypothesis quality and downstream usage. Further analysis shows the result is consistent across various label formats with different label configurations, and prior is hard to override, even under flipped labeling. These insights advance our understanding of the dynamics of hypothesis generation in LLMs and highlight the potential for better utilizing model priors in real-world inductive reasoning tasks.

CMM-Math: A Chinese Multimodal Math Dataset To Evaluate and Enhance the Mathematics Reasoning of Large Multimodal Models

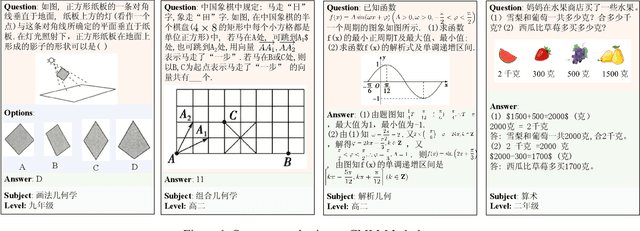
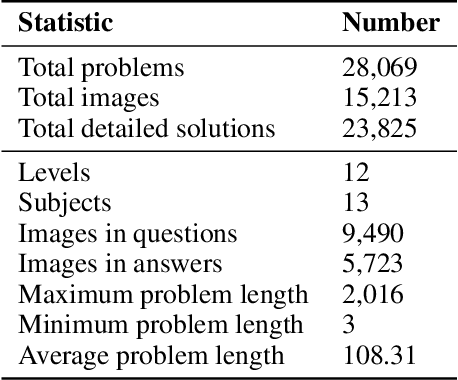
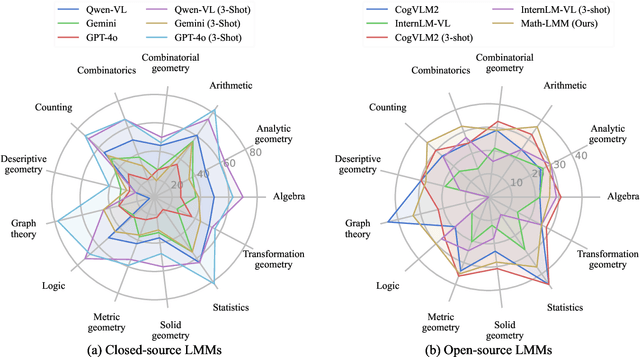
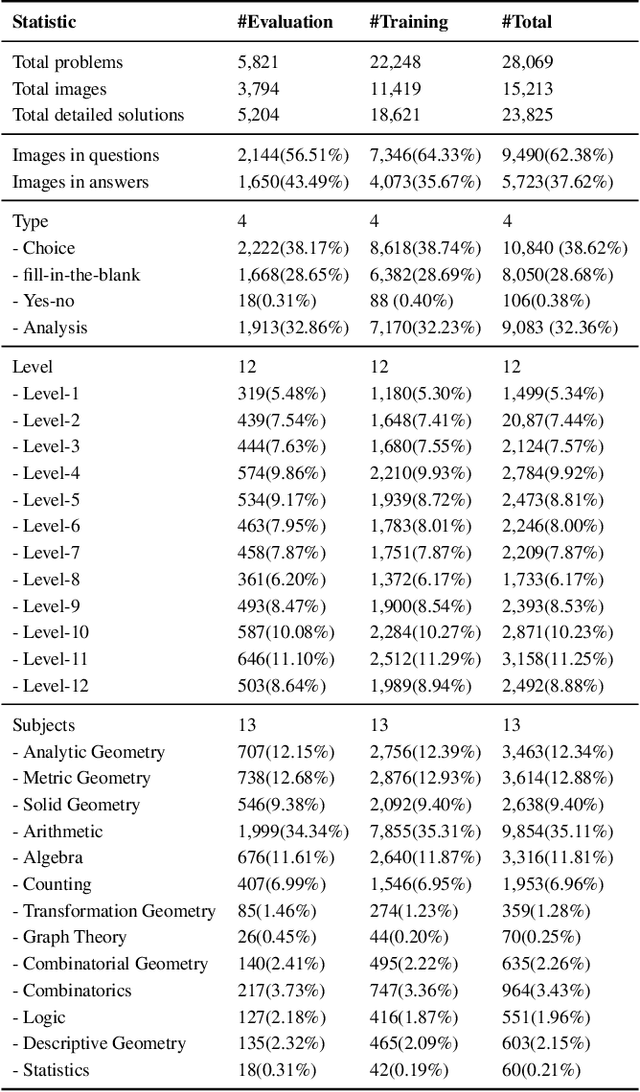
Large language models (LLMs) have obtained promising results in mathematical reasoning, which is a foundational skill for human intelligence. Most previous studies focus on improving and measuring the performance of LLMs based on textual math reasoning datasets (e.g., MATH, GSM8K). Recently, a few researchers have released English multimodal math datasets (e.g., MATHVISTA and MATH-V) to evaluate the effectiveness of large multimodal models (LMMs). In this paper, we release a Chinese multimodal math (CMM-Math) dataset, including benchmark and training parts, to evaluate and enhance the mathematical reasoning of LMMs. CMM-Math contains over 28,000 high-quality samples, featuring a variety of problem types (e.g., multiple-choice, fill-in-the-blank, and so on) with detailed solutions across 12 grade levels from elementary to high school in China. Specifically, the visual context may be present in the questions or opinions, which makes this dataset more challenging. Through comprehensive analysis, we discover that state-of-the-art LMMs on the CMM-Math dataset face challenges, emphasizing the necessity for further improvements in LMM development. We also propose a Multimodal Mathematical LMM (Math-LMM) to handle the problems with mixed input of multiple images and text segments. We train our model using three stages, including foundational pre-training, foundational fine-tuning, and mathematical fine-tuning. The extensive experiments indicate that our model effectively improves math reasoning performance by comparing it with the SOTA LMMs over three multimodal mathematical datasets.

Learning to Transform Dynamically for Better Adversarial Transferability

Adversarial examples, crafted by adding perturbations imperceptible to humans, can deceive neural networks. Recent studies identify the adversarial transferability across various models, \textit{i.e.}, the cross-model attack ability of adversarial samples. To enhance such adversarial transferability, existing input transformation-based methods diversify input data with transformation augmentation. However, their effectiveness is limited by the finite number of available transformations. In our study, we introduce a novel approach named Learning to Transform (L2T). L2T increases the diversity of transformed images by selecting the optimal combination of operations from a pool of candidates, consequently improving adversarial transferability. We conceptualize the selection of optimal transformation combinations as a trajectory optimization problem and employ a reinforcement learning strategy to effectively solve the problem. Comprehensive experiments on the ImageNet dataset, as well as practical tests with Google Vision and GPT-4V, reveal that L2T surpasses current methodologies in enhancing adversarial transferability, thereby confirming its effectiveness and practical significance. The code is available at https://github.com/RongyiZhu/L2T.

Approximated Likelihood Ratio: A Forward-Only and Parallel Framework for Boosting Neural Network Training

Efficient and biologically plausible alternatives to backpropagation in neural network training remain a challenge due to issues such as high computational complexity and additional assumptions about neural networks, which limit scalability to deeper networks. The likelihood ratio method offers a promising gradient estimation strategy but is constrained by significant memory consumption, especially when deploying multiple copies of data to reduce estimation variance. In this paper, we introduce an approximation technique for the likelihood ratio (LR) method to alleviate computational and memory demands in gradient estimation. By exploiting the natural parallelism during the backward pass using LR, we further provide a high-performance training strategy, which pipelines both the forward and backward pass, to make it more suitable for the computation on specialized hardware. Extensive experiments demonstrate the effectiveness of the approximation technique in neural network training. This work underscores the potential of the likelihood ratio method in achieving high-performance neural network training, suggesting avenues for further exploration.

CoRMF: Criticality-Ordered Recurrent Mean Field Ising Solver

We propose an RNN-based efficient Ising model solver, the Criticality-ordered Recurrent Mean Field (CoRMF), for forward Ising problems. In its core, a criticality-ordered spin sequence of an $N$-spin Ising model is introduced by sorting mission-critical edges with greedy algorithm, such that an autoregressive mean-field factorization can be utilized and optimized with Recurrent Neural Networks (RNNs). Our method has two notable characteristics: (i) by leveraging the approximated tree structure of the underlying Ising graph, the newly-obtained criticality order enables the unification between variational mean-field and RNN, allowing the generally intractable Ising model to be efficiently probed with probabilistic inference; (ii) it is well-modulized, model-independent while at the same time expressive enough, and hence fully applicable to any forward Ising inference problems with minimal effort. Computationally, by using a variance-reduced Monte Carlo gradient estimator, CoRFM solves the Ising problems in a self-train fashion without data/evidence, and the inference tasks can be executed by directly sampling from RNN. Theoretically, we establish a provably tighter error bound than naive mean-field by using the matrix cut decomposition machineries. Numerically, we demonstrate the utility of this framework on a series of Ising datasets.