Performance Analysis of Deep Learning Models for Femur Segmentation in MRI Scan

Convolutional neural networks like U-Net excel in medical image segmentation, while attention mechanisms and KAN enhance feature extraction. Meta's SAM 2 uses Vision Transformers for prompt-based segmentation without fine-tuning. However, biases in these models impact generalization with limited data. In this study, we systematically evaluate and compare the performance of three CNN-based models, i.e., U-Net, Attention U-Net, and U-KAN, and one transformer-based model, i.e., SAM 2 for segmenting femur bone structures in MRI scan. The dataset comprises 11,164 MRI scans with detailed annotations of femoral regions. Performance is assessed using the Dice Similarity Coefficient, which ranges from 0.932 to 0.954. Attention U-Net achieves the highest overall scores, while U-KAN demonstrated superior performance in anatomical regions with a smaller region of interest, leveraging its enhanced learning capacity to improve segmentation accuracy.

STGA: Selective-Training Gaussian Head Avatars

We propose selective-training Gaussian head avatars (STGA) to enhance the details of dynamic head Gaussian. The dynamic head Gaussian model is trained based on the FLAME parameterized model. Each Gaussian splat is embedded within the FLAME mesh to achieve mesh-based animation of the Gaussian model. Before training, our selection strategy calculates the 3D Gaussian splat to be optimized in each frame. The parameters of these 3D Gaussian splats are optimized in the training of each frame, while those of the other splats are frozen. This means that the splats participating in the optimization process differ in each frame, to improve the realism of fine details. Compared with network-based methods, our method achieves better results with shorter training time. Compared with mesh-based methods, our method produces more realistic details within the same training time. Additionally, the ablation experiment confirms that our method effectively enhances the quality of details.

RIFLEx: A Free Lunch for Length Extrapolation in Video Diffusion Transformers

Recent advancements in video generation have enabled models to synthesize high-quality, minute-long videos. However, generating even longer videos with temporal coherence remains a major challenge, and existing length extrapolation methods lead to temporal repetition or motion deceleration. In this work, we systematically analyze the role of frequency components in positional embeddings and identify an intrinsic frequency that primarily governs extrapolation behavior. Based on this insight, we propose RIFLEx, a minimal yet effective approach that reduces the intrinsic frequency to suppress repetition while preserving motion consistency, without requiring any additional modifications. RIFLEx offers a true free lunch--achieving high-quality $2\times$ extrapolation on state-of-the-art video diffusion transformers in a completely training-free manner. Moreover, it enhances quality and enables $3\times$ extrapolation by minimal fine-tuning without long videos. Project page and codes: \href{https://riflex-video.github.io/}{https://riflex-video.github.io/.}

Dual-Flow: Transferable Multi-Target, Instance-Agnostic Attacks via In-the-wild Cascading Flow Optimization

Adversarial attacks are widely used to evaluate model robustness, and in black-box scenarios, the transferability of these attacks becomes crucial. Existing generator-based attacks have excellent generalization and transferability due to their instance-agnostic nature. However, when training generators for multi-target tasks, the success rate of transfer attacks is relatively low due to the limitations of the model's capacity. To address these challenges, we propose a novel Dual-Flow framework for multi-target instance-agnostic adversarial attacks, utilizing Cascading Distribution Shift Training to develop an adversarial velocity function. Extensive experiments demonstrate that Dual-Flow significantly improves transferability over previous multi-target generative attacks. For example, it increases the success rate from Inception-v3 to ResNet-152 by 34.58%. Furthermore, our attack method shows substantially stronger robustness against defense mechanisms, such as adversarially trained models.

CITER: Collaborative Inference for Efficient Large Language Model Decoding with Token-Level Routing

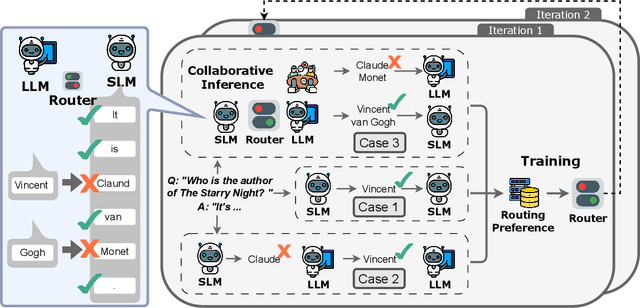
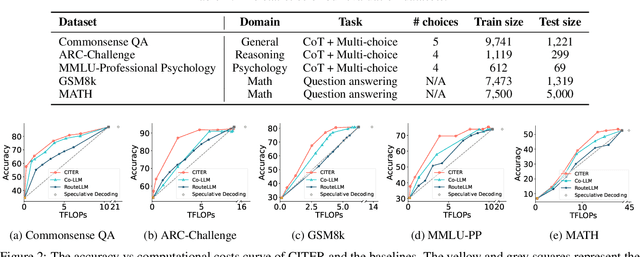
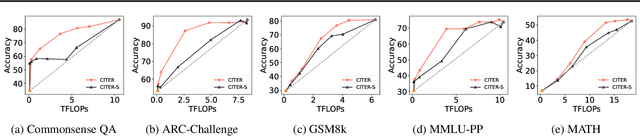
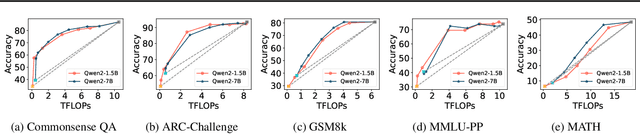
Large language models have achieved remarkable success in various tasks but suffer from high computational costs during inference, limiting their deployment in resource-constrained applications. To address this issue, we propose a novel CITER (\textbf{C}ollaborative \textbf{I}nference with \textbf{T}oken-l\textbf{E}vel \textbf{R}outing) framework that enables efficient collaboration between small and large language models (SLMs & LLMs) through a token-level routing strategy. Specifically, CITER routes non-critical tokens to an SLM for efficiency and routes critical tokens to an LLM for generalization quality. We formulate router training as a policy optimization, where the router receives rewards based on both the quality of predictions and the inference costs of generation. This allows the router to learn to predict token-level routing scores and make routing decisions based on both the current token and the future impact of its decisions. To further accelerate the reward evaluation process, we introduce a shortcut which significantly reduces the costs of the reward estimation and improving the practicality of our approach. Extensive experiments on five benchmark datasets demonstrate that CITER reduces the inference costs while preserving high-quality generation, offering a promising solution for real-time and resource-constrained applications.

Unsupervised Search for Ethnic Minorities' Medical Segmentation Training Set

This article investigates the critical issue of dataset bias in medical imaging, with a particular emphasis on racial disparities caused by uneven population distribution in dataset collection. Our analysis reveals that medical segmentation datasets are significantly biased, primarily influenced by the demographic composition of their collection sites. For instance, Scanning Laser Ophthalmoscopy (SLO) fundus datasets collected in the United States predominantly feature images of White individuals, with minority racial groups underrepresented. This imbalance can result in biased model performance and inequitable clinical outcomes, particularly for minority populations. To address this challenge, we propose a novel training set search strategy aimed at reducing these biases by focusing on underrepresented racial groups. Our approach utilizes existing datasets and employs a simple greedy algorithm to identify source images that closely match the target domain distribution. By selecting training data that aligns more closely with the characteristics of minority populations, our strategy improves the accuracy of medical segmentation models on specific minorities, i.e., Black. Our experimental results demonstrate the effectiveness of this approach in mitigating bias. We also discuss the broader societal implications, highlighting how addressing these disparities can contribute to more equitable healthcare outcomes.

Ground state phases of the two-dimension electron gas with a unified variational approach

The two-dimensional electron gas (2DEG) is a fundamental model, which is drawing increasing interest because of recent advances in experimental and theoretical studies of 2D materials. Current understanding of the ground state of the 2DEG relies on quantum Monte Carlo calculations, based on variational comparisons of different ansatze for different phases. We use a single variational ansatz, a general backflow-type wave function using a message-passing neural quantum state architecture, for a unified description across the entire density range. The variational optimization consistently leads to lower ground-state energies than previous best results. Transition into a Wigner crystal (WC) phase occurs automatically at rs = 37 +/- 1, a density lower than currently believed. Between the liquid and WC phases, the same ansatz and variational search strongly suggest the existence of intermediate states in a broad range of densities, with enhanced short-range nematic spin correlations.

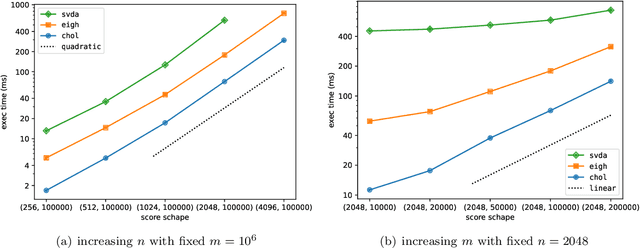
Efficient Numerical Algorithm for Large-Scale Damped Natural Gradient Descent

We propose a new algorithm for efficiently solving the damped Fisher matrix in large-scale scenarios where the number of parameters significantly exceeds the number of available samples. This problem is fundamental for natural gradient descent and stochastic reconfiguration. Our algorithm is based on Cholesky decomposition and is generally applicable. Benchmark results show that the algorithm is significantly faster than existing methods.

DeePKS+ABACUS as a Bridge between Expensive Quantum Mechanical Models and Machine Learning Potentials

Recently, the development of machine learning (ML) potentials has made it possible to perform large-scale and long-time molecular simulations with the accuracy of quantum mechanical (QM) models. However, for high-level QM methods, such as density functional theory (DFT) at the meta-GGA level and/or with exact exchange, quantum Monte Carlo, etc., generating a sufficient amount of data for training a ML potential has remained computationally challenging due to their high cost. In this work, we demonstrate that this issue can be largely alleviated with Deep Kohn-Sham (DeePKS), a ML-based DFT model. DeePKS employs a computationally efficient neural network-based functional model to construct a correction term added upon a cheap DFT model. Upon training, DeePKS offers closely-matched energies and forces compared with high-level QM method, but the number of training data required is orders of magnitude less than that required for training a reliable ML potential. As such, DeePKS can serve as a bridge between expensive QM models and ML potentials: one can generate a decent amount of high-accuracy QM data to train a DeePKS model, and then use the DeePKS model to label a much larger amount of configurations to train a ML potential. This scheme for periodic systems is implemented in a DFT package ABACUS, which is open-source and ready for use in various applications.

DeePKS: a comprehensive data-driven approach towards chemically accurate density functional theory

We propose a general machine learning-based framework for building an accurate and widely-applicable energy functional within the framework of generalized Kohn-Sham density functional theory. To this end, we develop a way of training self-consistent models that are capable of taking large datasets from different systems and different kinds of labels. We demonstrate that the functional that results from this training procedure gives chemically accurate predictions on energy, force, dipole, and electron density for a large class of molecules. It can be continuously improved when more and more data are available.