Efficient Numerical Algorithm for Large-Scale Damped Natural Gradient Descent
Paper and Code
Oct 26, 2023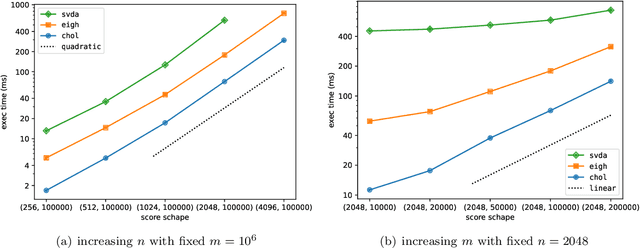

We propose a new algorithm for efficiently solving the damped Fisher matrix in large-scale scenarios where the number of parameters significantly exceeds the number of available samples. This problem is fundamental for natural gradient descent and stochastic reconfiguration. Our algorithm is based on Cholesky decomposition and is generally applicable. Benchmark results show that the algorithm is significantly faster than existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge