EoRA: Training-free Compensation for Compressed LLM with Eigenspace Low-Rank Approximation

In this work, we re-formulate the model compression problem into the customized compensation problem: Given a compressed model, we aim to introduce residual low-rank paths to compensate for compression errors under customized requirements from users (e.g., tasks, compression ratios), resulting in greater flexibility in adjusting overall capacity without being constrained by specific compression formats. However, naively applying SVD to derive residual paths causes suboptimal utilization of the low-rank representation capacity. Instead, we propose Training-free Eigenspace Low-Rank Approximation (EoRA), a method that directly minimizes compression-induced errors without requiring gradient-based training, achieving fast optimization in minutes using a small amount of calibration data. EoRA projects compression errors into the eigenspace of input activations, leveraging eigenvalues to effectively prioritize the reconstruction of high-importance error components. Moreover, EoRA can be seamlessly integrated with fine-tuning and quantization to further improve effectiveness and efficiency. EoRA consistently outperforms previous methods in compensating errors for compressed LLaMA2/3 models on various tasks, such as language generation, commonsense reasoning, and math reasoning tasks (e.g., 31.31%/12.88% and 9.69% improvements on ARC-Easy/ARC-Challenge and MathQA when compensating LLaMA3-8B that is quantized to 4-bit and pruned to 2:4 sparsity). EoRA offers a scalable, training-free solution to compensate for compression errors, making it a powerful tool to deploy LLMs in various capacity and efficiency requirements.

ESPACE: Dimensionality Reduction of Activations for Model Compression

We propose ESPACE, an LLM compression technique based on dimensionality reduction of activations. Unlike prior works on weight-centric tensor decomposition, ESPACE projects activations onto a pre-calibrated set of principal components. The activation-centrality of the approach enables retraining LLMs with no loss of expressivity; while at inference, weight decomposition is obtained as a byproduct of matrix multiplication associativity. Theoretical results on the construction of projection matrices with optimal computational accuracy are provided. Experimentally, we find ESPACE enables 50% compression of GPT3, Llama2, and Nemotron4 models with small accuracy degradation, as low as a 0.18 perplexity increase on GPT3-22B. At lower compression rates of 20% to 40%, ESPACE drives GPT3 models to outperforming their baseline, by up to a 0.38 decrease in perplexity for GPT3-8B. ESPACE also reduces GEMM execution time and prefill inference latency on existing hardware. Comparison with related works on compressing Llama2-7B via matrix factorization shows that ESPACE is a first step in advancing the state-of-the-art in tensor decomposition compression of LLMs.

VaPr: Variable-Precision Tensors to Accelerate Robot Motion Planning

High-dimensional motion generation requires numerical precision for smooth, collision-free solutions. Typically, double-precision or single-precision floating-point (FP) formats are utilized. Using these for big tensors imposes a strain on the memory bandwidth provided by the devices and alters the memory footprint, hence limiting their applicability to low-power edge devices needed for mobile robots. The uniform application of reduced precision can be advantageous but severely degrades solutions. Using decreased precision data types for important tensors, we propose to accelerate motion generation by removing memory bottlenecks. We propose variable-precision (VaPr) search optimization to determine the appropriate precision for large tensors from a vast search space of approximately 4 million unique combinations for FP data types across the tensors. To obtain the efficiency gains, we exploit existing platform support for an out-of-the-box GPU speedup and evaluate prospective precision converter units for GPU types that are not currently supported. Our experimental results on 800 planning problems for the Franka Panda robot on the MotionBenchmaker dataset across 8 environments show that a 4-bit FP format is sufficient for the largest set of tensors in the motion generation stack. With the software-only solution, VaPr achieves 6.3% and 6.3% speedups on average for a significant portion of motion generation over the SOTA solution (CuRobo) on Jetson Orin and RTX2080 Ti GPU, respectively, and 9.9%, 17.7% speedups with the FP converter.

Optimal Clipping and Magnitude-aware Differentiation for Improved Quantization-aware Training

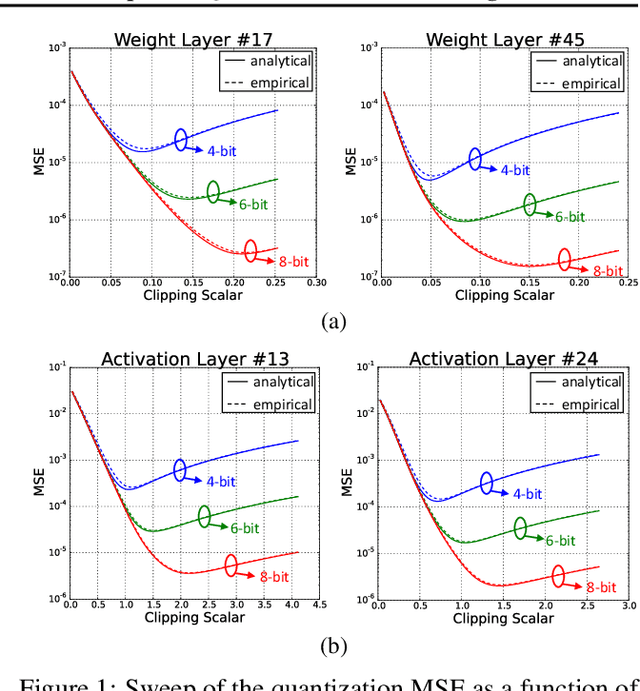
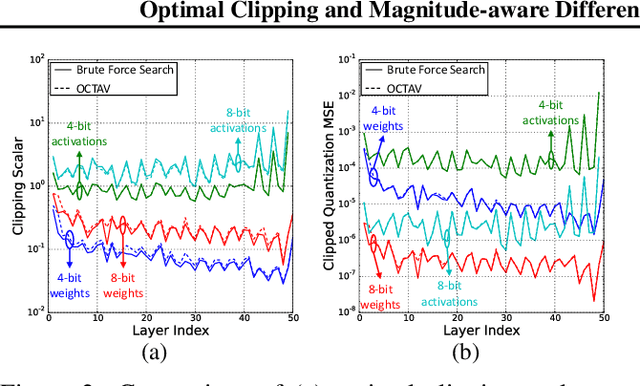
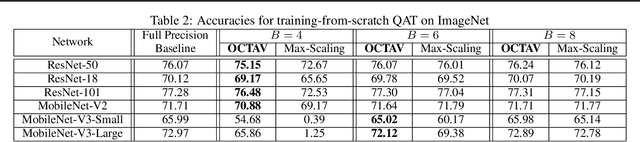
Data clipping is crucial in reducing noise in quantization operations and improving the achievable accuracy of quantization-aware training (QAT). Current practices rely on heuristics to set clipping threshold scalars and cannot be shown to be optimal. We propose Optimally Clipped Tensors And Vectors (OCTAV), a recursive algorithm to determine MSE-optimal clipping scalars. Derived from the fast Newton-Raphson method, OCTAV finds optimal clipping scalars on the fly, for every tensor, at every iteration of the QAT routine. Thus, the QAT algorithm is formulated with provably minimum quantization noise at each step. In addition, we reveal limitations in common gradient estimation techniques in QAT and propose magnitude-aware differentiation as a remedy to further improve accuracy. Experimentally, OCTAV-enabled QAT achieves state-of-the-art accuracy on multiple tasks. These include training-from-scratch and retraining ResNets and MobileNets on ImageNet, and Squad fine-tuning using BERT models, where OCTAV-enabled QAT consistently preserves accuracy at low precision (4-to-6-bits). Our results require no modifications to the baseline training recipe, except for the insertion of quantization operations where appropriate.

Fundamental Limits on Energy-Delay-Accuracy of In-memory Architectures in Inference Applications

This paper obtains fundamental limits on the computational precision of in-memory computing architectures (IMCs). An IMC noise model and associated SNR metrics are defined and their interrelationships analyzed to show that the accuracy of IMCs is fundamentally limited by the compute SNR ($\text{SNR}_{\text{a}}$) of its analog core, and that activation, weight and output precision needs to be assigned appropriately for the final output SNR $\text{SNR}_{\text{T}} \rightarrow \text{SNR}_{\text{a}}$. The minimum precision criterion (MPC) is proposed to minimize the ADC precision. Three in-memory compute models - charge summing (QS), current summing (IS) and charge redistribution (QR) - are shown to underlie most known IMCs. Noise, energy and delay expressions for the compute models are developed and employed to derive expressions for the SNR, ADC precision, energy, and latency of IMCs. The compute SNR expressions are validated via Monte Carlo simulations in a 65 nm CMOS process. For a 512 row SRAM array, it is shown that: 1) IMCs have an upper bound on their maximum achievable $\text{SNR}_{\text{a}}$ due to constraints on energy, area and voltage swing, and this upper bound reduces with technology scaling for QS-based architectures; 2) MPC enables $\text{SNR}_{\text{T}} \rightarrow \text{SNR}_{\text{a}}$ to be realized with minimal ADC precision; 3) QS-based (QR-based) architectures are preferred for low (high) compute SNR scenarios.

HarDNN: Feature Map Vulnerability Evaluation in CNNs

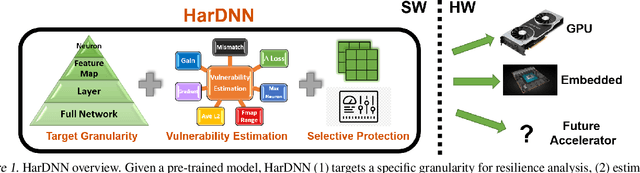
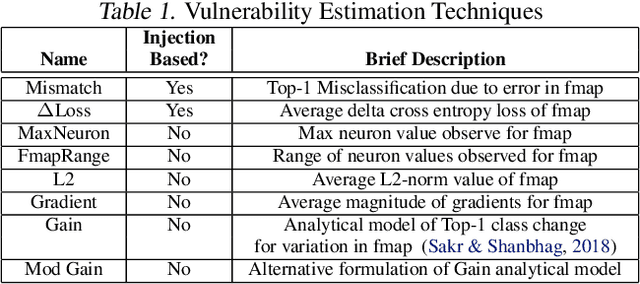
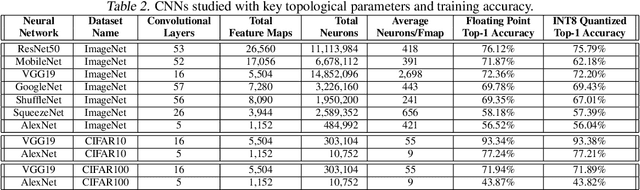
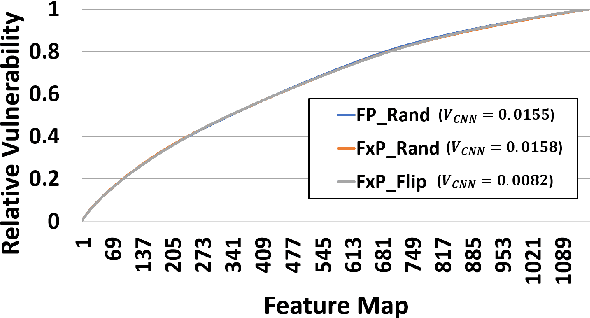
As Convolutional Neural Networks (CNNs) are increasingly being employed in safety-critical applications, it is important that they behave reliably in the face of hardware errors. Transient hardware errors may percolate undesirable state during execution, resulting in software-manifested errors which can adversely affect high-level decision making. This paper presents HarDNN, a software-directed approach to identify vulnerable computations during a CNN inference and selectively protect them based on their propensity towards corrupting the inference output in the presence of a hardware error. We show that HarDNN can accurately estimate relative vulnerability of a feature map (fmap) in CNNs using a statistical error injection campaign, and explore heuristics for fast vulnerability assessment. Based on these results, we analyze the tradeoff between error coverage and computational overhead that the system designers can use to employ selective protection. Results show that the improvement in resilience for the added computation is superlinear with HarDNN. For example, HarDNN improves SqueezeNet's resilience by 10x with just 30% additional computations.

Accumulation Bit-Width Scaling For Ultra-Low Precision Training Of Deep Networks

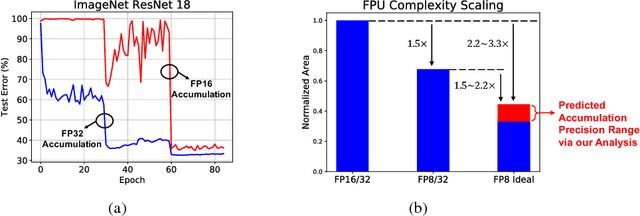
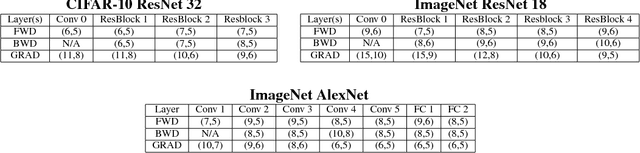
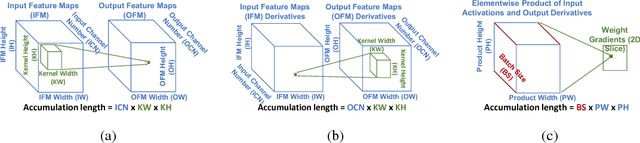
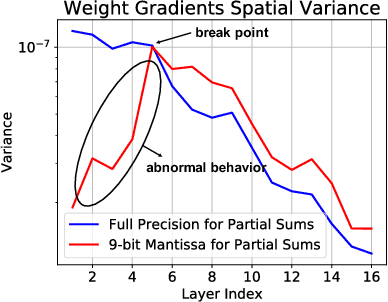
Efforts to reduce the numerical precision of computations in deep learning training have yielded systems that aggressively quantize weights and activations, yet employ wide high-precision accumulators for partial sums in inner-product operations to preserve the quality of convergence. The absence of any framework to analyze the precision requirements of partial sum accumulations results in conservative design choices. This imposes an upper-bound on the reduction of complexity of multiply-accumulate units. We present a statistical approach to analyze the impact of reduced accumulation precision on deep learning training. Observing that a bad choice for accumulation precision results in loss of information that manifests itself as a reduction in variance in an ensemble of partial sums, we derive a set of equations that relate this variance to the length of accumulation and the minimum number of bits needed for accumulation. We apply our analysis to three benchmark networks: CIFAR-10 ResNet 32, ImageNet ResNet 18 and ImageNet AlexNet. In each case, with accumulation precision set in accordance with our proposed equations, the networks successfully converge to the single precision floating-point baseline. We also show that reducing accumulation precision further degrades the quality of the trained network, proving that our equations produce tight bounds. Overall this analysis enables precise tailoring of computation hardware to the application, yielding area- and power-optimal systems.

Per-Tensor Fixed-Point Quantization of the Back-Propagation Algorithm

The high computational and parameter complexity of neural networks makes their training very slow and difficult to deploy on energy and storage-constrained computing systems. Many network complexity reduction techniques have been proposed including fixed-point implementation. However, a systematic approach for designing full fixed-point training and inference of deep neural networks remains elusive. We describe a precision assignment methodology for neural network training in which all network parameters, i.e., activations and weights in the feedforward path, gradients and weight accumulators in the feedback path, are assigned close to minimal precision. The precision assignment is derived analytically and enables tracking the convergence behavior of the full precision training, known to converge a priori. Thus, our work leads to a systematic methodology of determining suitable precision for fixed-point training. The near optimality (minimality) of the resulting precision assignment is validated empirically for four networks on the CIFAR-10, CIFAR-100, and SVHN datasets. The complexity reduction arising from our approach is compared with other fixed-point neural network designs.

Understanding the Energy and Precision Requirements for Online Learning

It is well-known that the precision of data, hyperparameters, and internal representations employed in learning systems directly impacts its energy, throughput, and latency. The precision requirements for the training algorithm are also important for systems that learn on-the-fly. Prior work has shown that the data and hyperparameters can be quantized heavily without incurring much penalty in classification accuracy when compared to floating point implementations. These works suffer from two key limitations. First, they assume uniform precision for the classifier and for the training algorithm and thus miss out on the opportunity to further reduce precision. Second, prior works are empirical studies. In this article, we overcome both these limitations by deriving analytical lower bounds on the precision requirements of the commonly employed stochastic gradient descent (SGD) on-line learning algorithm in the specific context of a support vector machine (SVM). Lower bounds on the data precision are derived in terms of the the desired classification accuracy and precision of the hyperparameters used in the classifier. Additionally, lower bounds on the hyperparameter precision in the SGD training algorithm are obtained. These bounds are validated using both synthetic and the UCI breast cancer dataset. Additionally, the impact of these precisions on the energy consumption of a fixed-point SVM with on-line training is studied.