Accumulation Bit-Width Scaling For Ultra-Low Precision Training Of Deep Networks

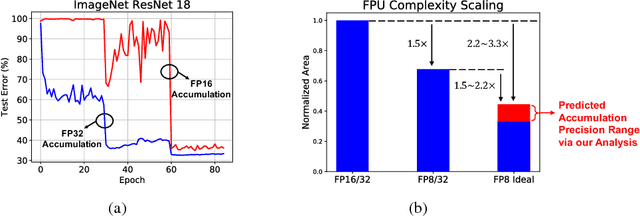
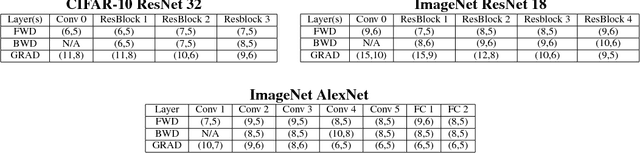
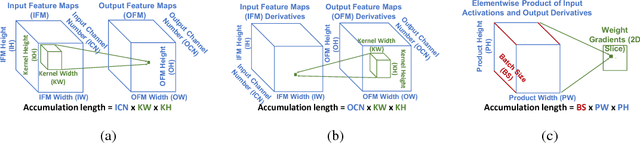
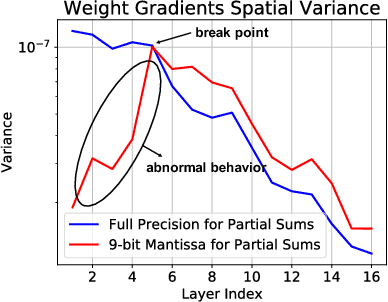
Efforts to reduce the numerical precision of computations in deep learning training have yielded systems that aggressively quantize weights and activations, yet employ wide high-precision accumulators for partial sums in inner-product operations to preserve the quality of convergence. The absence of any framework to analyze the precision requirements of partial sum accumulations results in conservative design choices. This imposes an upper-bound on the reduction of complexity of multiply-accumulate units. We present a statistical approach to analyze the impact of reduced accumulation precision on deep learning training. Observing that a bad choice for accumulation precision results in loss of information that manifests itself as a reduction in variance in an ensemble of partial sums, we derive a set of equations that relate this variance to the length of accumulation and the minimum number of bits needed for accumulation. We apply our analysis to three benchmark networks: CIFAR-10 ResNet 32, ImageNet ResNet 18 and ImageNet AlexNet. In each case, with accumulation precision set in accordance with our proposed equations, the networks successfully converge to the single precision floating-point baseline. We also show that reducing accumulation precision further degrades the quality of the trained network, proving that our equations produce tight bounds. Overall this analysis enables precise tailoring of computation hardware to the application, yielding area- and power-optimal systems.

AdaComp : Adaptive Residual Gradient Compression for Data-Parallel Distributed Training

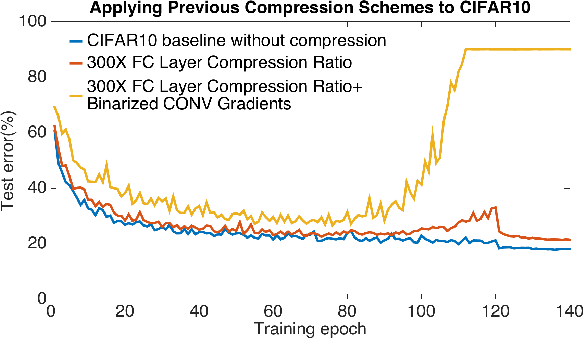
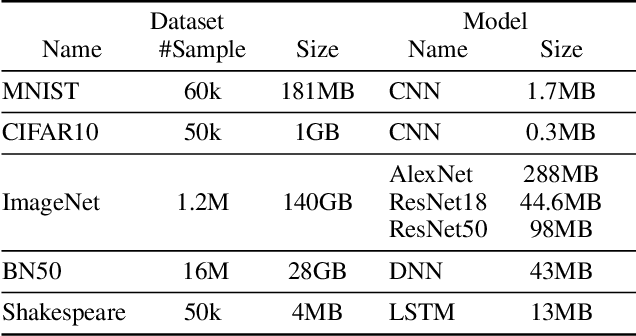
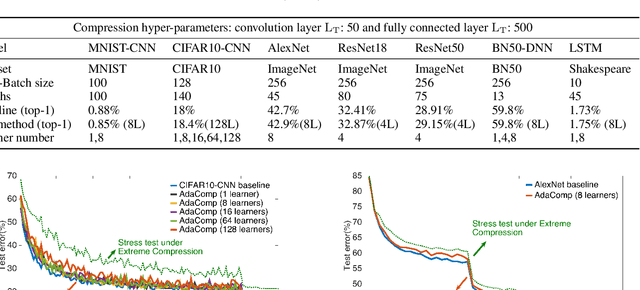
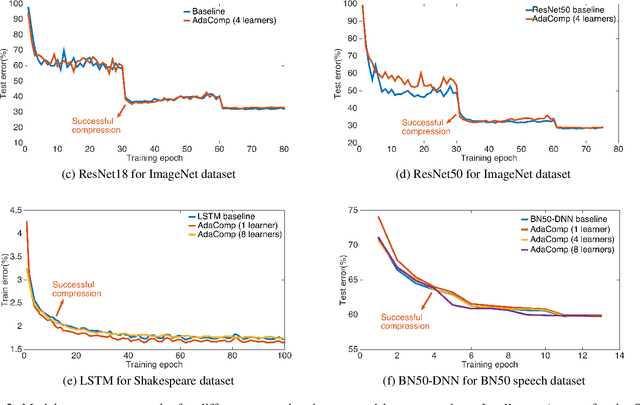
Highly distributed training of Deep Neural Networks (DNNs) on future compute platforms (offering 100 of TeraOps/s of computational capacity) is expected to be severely communication constrained. To overcome this limitation, new gradient compression techniques are needed that are computationally friendly, applicable to a wide variety of layers seen in Deep Neural Networks and adaptable to variations in network architectures as well as their hyper-parameters. In this paper we introduce a novel technique - the Adaptive Residual Gradient Compression (AdaComp) scheme. AdaComp is based on localized selection of gradient residues and automatically tunes the compression rate depending on local activity. We show excellent results on a wide spectrum of state of the art Deep Learning models in multiple domains (vision, speech, language), datasets (MNIST, CIFAR10, ImageNet, BN50, Shakespeare), optimizers (SGD with momentum, Adam) and network parameters (number of learners, minibatch-size etc.). Exploiting both sparsity and quantization, we demonstrate end-to-end compression rates of ~200X for fully-connected and recurrent layers, and ~40X for convolutional layers, without any noticeable degradation in model accuracies.

Deep Learning with Limited Numerical Precision

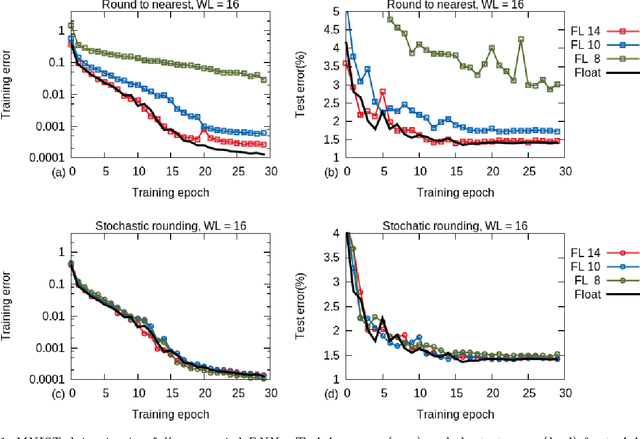
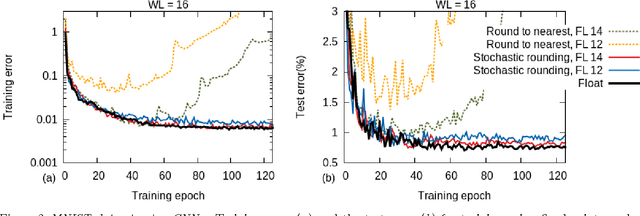
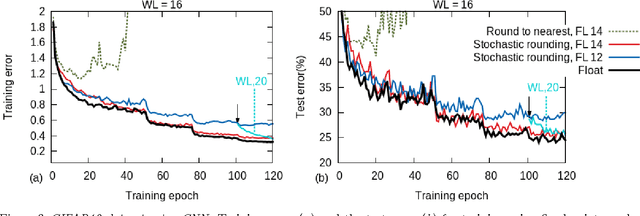
Training of large-scale deep neural networks is often constrained by the available computational resources. We study the effect of limited precision data representation and computation on neural network training. Within the context of low-precision fixed-point computations, we observe the rounding scheme to play a crucial role in determining the network's behavior during training. Our results show that deep networks can be trained using only 16-bit wide fixed-point number representation when using stochastic rounding, and incur little to no degradation in the classification accuracy. We also demonstrate an energy-efficient hardware accelerator that implements low-precision fixed-point arithmetic with stochastic rounding.