Hardware-aware training for large-scale and diverse deep learning inference workloads using in-memory computing-based accelerators

Analog in-memory computing (AIMC) -- a promising approach for energy-efficient acceleration of deep learning workloads -- computes matrix-vector multiplications (MVMs) but only approximately, due to nonidealities that often are non-deterministic or nonlinear. This can adversely impact the achievable deep neural network (DNN) inference accuracy as compared to a conventional floating point (FP) implementation. While retraining has previously been suggested to improve robustness, prior work has explored only a few DNN topologies, using disparate and overly simplified AIMC hardware models. Here, we use hardware-aware (HWA) training to systematically examine the accuracy of AIMC for multiple common artificial intelligence (AI) workloads across multiple DNN topologies, and investigate sensitivity and robustness to a broad set of nonidealities. By introducing a new and highly realistic AIMC crossbar-model, we improve significantly on earlier retraining approaches. We show that many large-scale DNNs of various topologies, including convolutional neural networks (CNNs), recurrent neural networks (RNNs), and transformers, can in fact be successfully retrained to show iso-accuracy on AIMC. Our results further suggest that AIMC nonidealities that add noise to the inputs or outputs, not the weights, have the largest impact on DNN accuracy, and that RNNs are particularly robust to all nonidealities.

Deep Learning with Limited Numerical Precision

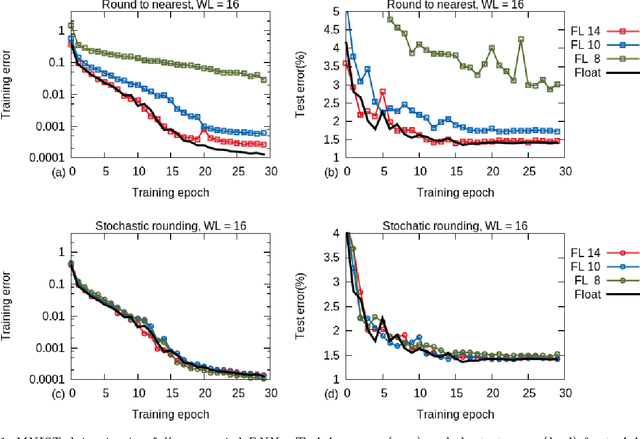
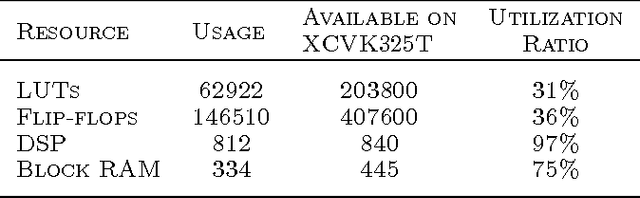
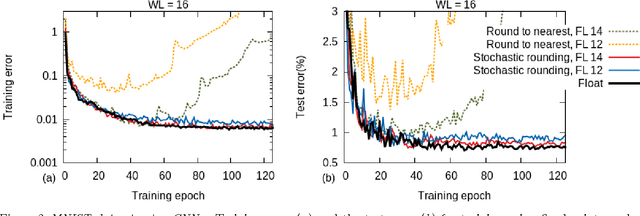
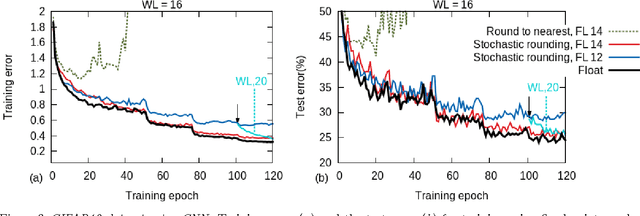
Training of large-scale deep neural networks is often constrained by the available computational resources. We study the effect of limited precision data representation and computation on neural network training. Within the context of low-precision fixed-point computations, we observe the rounding scheme to play a crucial role in determining the network's behavior during training. Our results show that deep networks can be trained using only 16-bit wide fixed-point number representation when using stochastic rounding, and incur little to no degradation in the classification accuracy. We also demonstrate an energy-efficient hardware accelerator that implements low-precision fixed-point arithmetic with stochastic rounding.