Accelerating Inference and Language Model Fusion of Recurrent Neural Network Transducers via End-to-End 4-bit Quantization

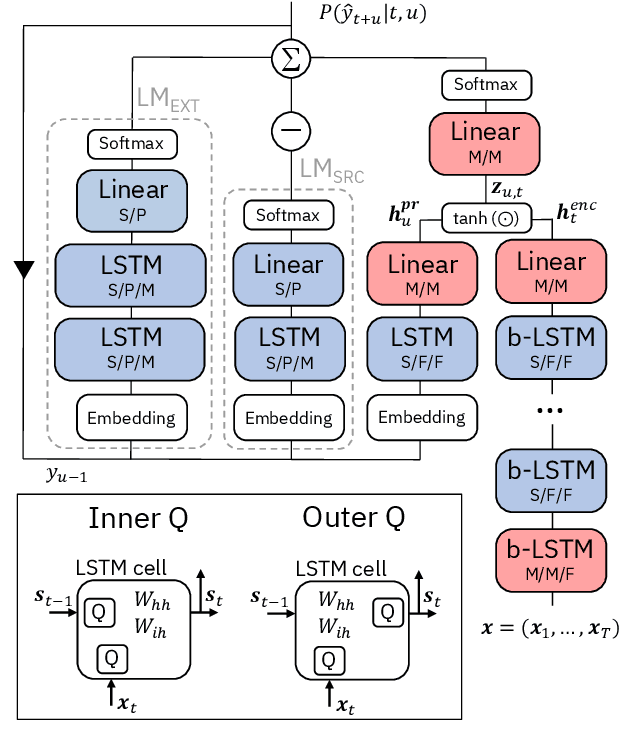
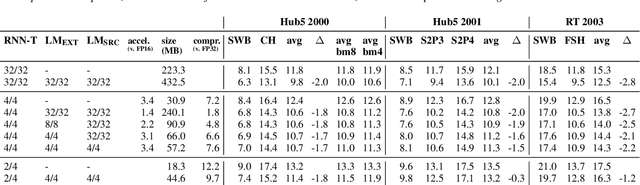
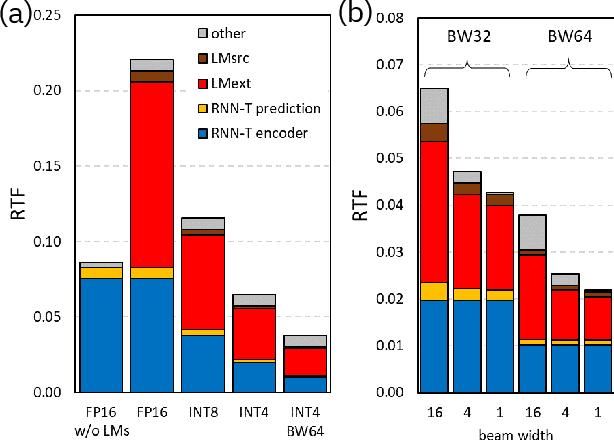
We report on aggressive quantization strategies that greatly accelerate inference of Recurrent Neural Network Transducers (RNN-T). We use a 4 bit integer representation for both weights and activations and apply Quantization Aware Training (QAT) to retrain the full model (acoustic encoder and language model) and achieve near-iso-accuracy. We show that customized quantization schemes that are tailored to the local properties of the network are essential to achieve good performance while limiting the computational overhead of QAT. Density ratio Language Model fusion has shown remarkable accuracy gains on RNN-T workloads but it severely increases the computational cost of inference. We show that our quantization strategies enable using large beam widths for hypothesis search while achieving streaming-compatible runtimes and a full model compression ratio of 7.6$\times$ compared to the full precision model. Via hardware simulations, we estimate a 3.4$\times$ acceleration from FP16 to INT4 for the end-to-end quantized RNN-T inclusive of LM fusion, resulting in a Real Time Factor (RTF) of 0.06. On the NIST Hub5 2000, Hub5 2001, and RT-03 test sets, we retain most of the gains associated with LM fusion, improving the average WER by $>$1.5%.

4-bit Quantization of LSTM-based Speech Recognition Models

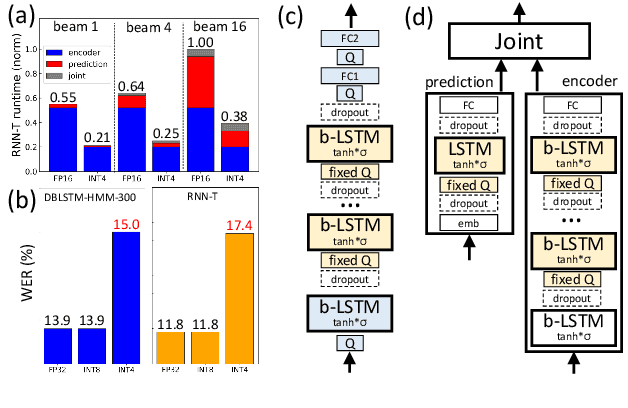
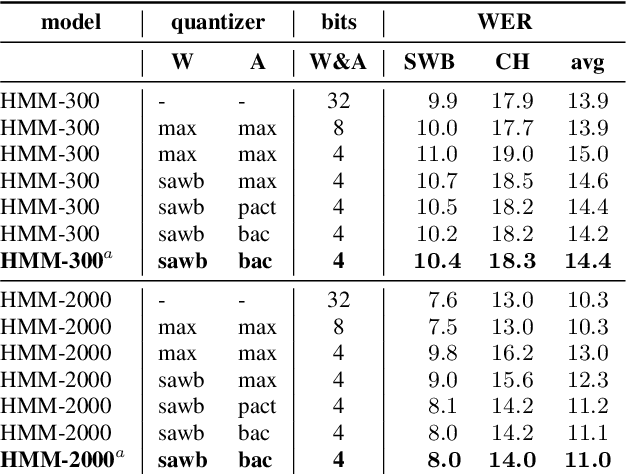
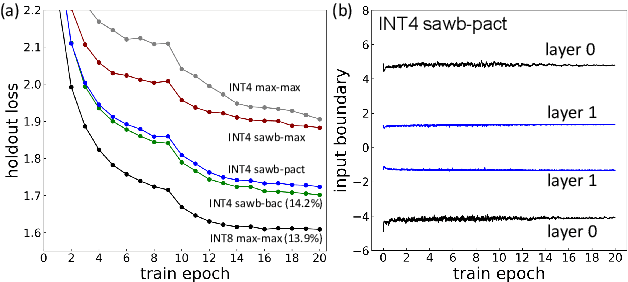
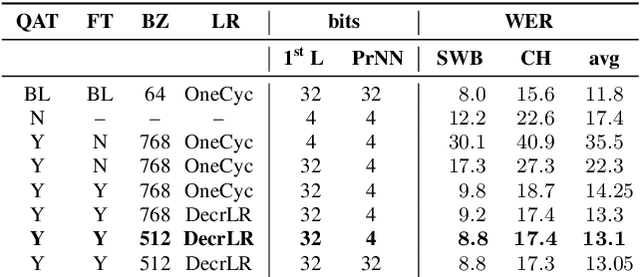
We investigate the impact of aggressive low-precision representations of weights and activations in two families of large LSTM-based architectures for Automatic Speech Recognition (ASR): hybrid Deep Bidirectional LSTM - Hidden Markov Models (DBLSTM-HMMs) and Recurrent Neural Network - Transducers (RNN-Ts). Using a 4-bit integer representation, a na\"ive quantization approach applied to the LSTM portion of these models results in significant Word Error Rate (WER) degradation. On the other hand, we show that minimal accuracy loss is achievable with an appropriate choice of quantizers and initializations. In particular, we customize quantization schemes depending on the local properties of the network, improving recognition performance while limiting computational time. We demonstrate our solution on the Switchboard (SWB) and CallHome (CH) test sets of the NIST Hub5-2000 evaluation. DBLSTM-HMMs trained with 300 or 2000 hours of SWB data achieves $<$0.5% and $<$1% average WER degradation, respectively. On the more challenging RNN-T models, our quantization strategy limits degradation in 4-bit inference to 1.3%.

ScaleCom: Scalable Sparsified Gradient Compression for Communication-Efficient Distributed Training

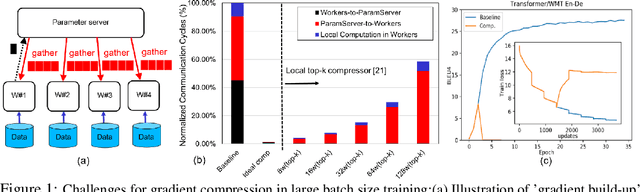
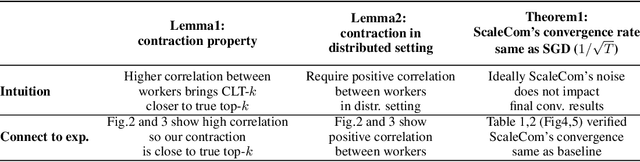
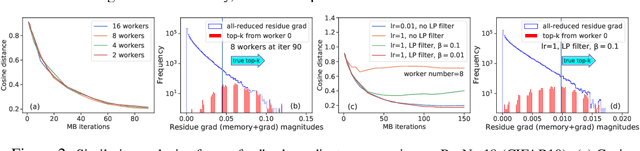
Large-scale distributed training of Deep Neural Networks (DNNs) on state-of-the-art platforms is expected to be severely communication constrained. To overcome this limitation, numerous gradient compression techniques have been proposed and have demonstrated high compression ratios. However, most existing methods do not scale well to large scale distributed systems (due to gradient build-up) and/or fail to evaluate model fidelity (test accuracy) on large datasets. To mitigate these issues, we propose a new compression technique, Scalable Sparsified Gradient Compression (ScaleCom), that leverages similarity in the gradient distribution amongst learners to provide significantly improved scalability. Using theoretical analysis, we show that ScaleCom provides favorable convergence guarantees and is compatible with gradient all-reduce techniques. Furthermore, we experimentally demonstrate that ScaleCom has small overheads, directly reduces gradient traffic and provides high compression rates (65-400X) and excellent scalability (up to 64 learners and 8-12X larger batch sizes over standard training) across a wide range of applications (image, language, and speech) without significant accuracy loss.

FracTrain: Fractionally Squeezing Bit Savings Both Temporally and Spatially for Efficient DNN Training

Recent breakthroughs in deep neural networks (DNNs) have fueled a tremendous demand for intelligent edge devices featuring on-site learning, while the practical realization of such systems remains a challenge due to the limited resources available at the edge and the required massive training costs for state-of-the-art (SOTA) DNNs. As reducing precision is one of the most effective knobs for boosting training time/energy efficiency, there has been a growing interest in low-precision DNN training. In this paper, we explore from an orthogonal direction: how to fractionally squeeze out more training cost savings from the most redundant bit level, progressively along the training trajectory and dynamically per input. Specifically, we propose FracTrain that integrates (i) progressive fractional quantization which gradually increases the precision of activations, weights, and gradients that will not reach the precision of SOTA static quantized DNN training until the final training stage, and (ii) dynamic fractional quantization which assigns precisions to both the activations and gradients of each layer in an input-adaptive manner, for only "fractionally" updating layer parameters. Extensive simulations and ablation studies (six models, four datasets, and three training settings including standard, adaptation, and fine-tuning) validate the effectiveness of FracTrain in reducing computational cost and hardware-quantified energy/latency of DNN training while achieving a comparable or better (-0.12%~+1.87%) accuracy. For example, when training ResNet-74 on CIFAR-10, FracTrain achieves 77.6% and 53.5% computational cost and training latency savings, respectively, compared with the best SOTA baseline, while achieving a comparable (-0.07%) accuracy. Our codes are available at: https://github.com/RICE-EIC/FracTrain.

Accumulation Bit-Width Scaling For Ultra-Low Precision Training Of Deep Networks

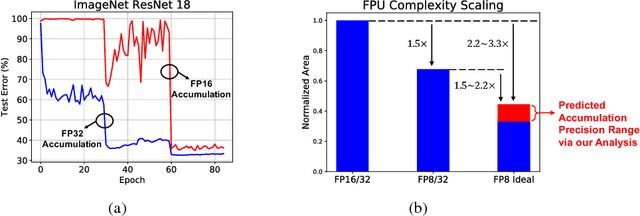
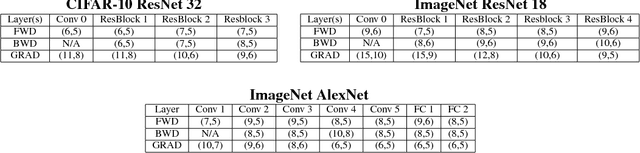
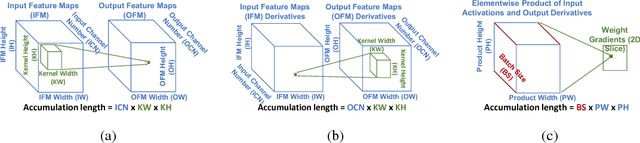
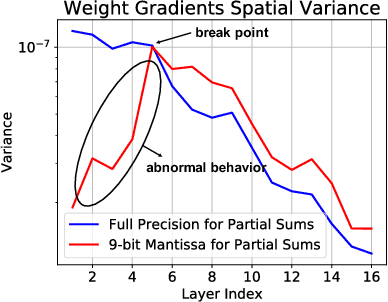
Efforts to reduce the numerical precision of computations in deep learning training have yielded systems that aggressively quantize weights and activations, yet employ wide high-precision accumulators for partial sums in inner-product operations to preserve the quality of convergence. The absence of any framework to analyze the precision requirements of partial sum accumulations results in conservative design choices. This imposes an upper-bound on the reduction of complexity of multiply-accumulate units. We present a statistical approach to analyze the impact of reduced accumulation precision on deep learning training. Observing that a bad choice for accumulation precision results in loss of information that manifests itself as a reduction in variance in an ensemble of partial sums, we derive a set of equations that relate this variance to the length of accumulation and the minimum number of bits needed for accumulation. We apply our analysis to three benchmark networks: CIFAR-10 ResNet 32, ImageNet ResNet 18 and ImageNet AlexNet. In each case, with accumulation precision set in accordance with our proposed equations, the networks successfully converge to the single precision floating-point baseline. We also show that reducing accumulation precision further degrades the quality of the trained network, proving that our equations produce tight bounds. Overall this analysis enables precise tailoring of computation hardware to the application, yielding area- and power-optimal systems.

Training Deep Neural Networks with 8-bit Floating Point Numbers

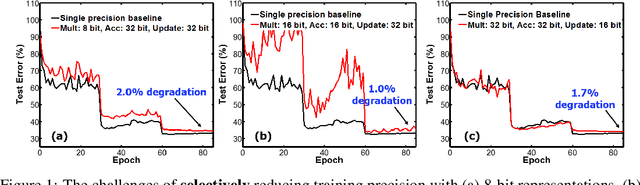
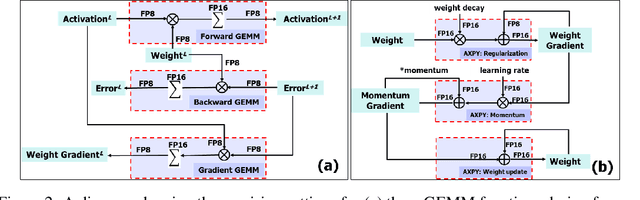
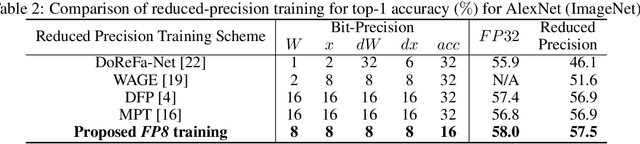
The state-of-the-art hardware platforms for training Deep Neural Networks (DNNs) are moving from traditional single precision (32-bit) computations towards 16 bits of precision -- in large part due to the high energy efficiency and smaller bit storage associated with using reduced-precision representations. However, unlike inference, training with numbers represented with less than 16 bits has been challenging due to the need to maintain fidelity of the gradient computations during back-propagation. Here we demonstrate, for the first time, the successful training of DNNs using 8-bit floating point numbers while fully maintaining the accuracy on a spectrum of Deep Learning models and datasets. In addition to reducing the data and computation precision to 8 bits, we also successfully reduce the arithmetic precision for additions (used in partial product accumulation and weight updates) from 32 bits to 16 bits through the introduction of a number of key ideas including chunk-based accumulation and floating point stochastic rounding. The use of these novel techniques lays the foundation for a new generation of hardware training platforms with the potential for 2-4x improved throughput over today's systems.

Bridging the Accuracy Gap for 2-bit Quantized Neural Networks

Deep learning algorithms achieve high classification accuracy at the expense of significant computation cost. In order to reduce this cost, several quantization schemes have gained attention recently with some focusing on weight quantization, and others focusing on quantizing activations. This paper proposes novel techniques that target weight and activation quantizations separately resulting in an overall quantized neural network (QNN). The activation quantization technique, PArameterized Clipping acTivation (PACT), uses an activation clipping parameter $\alpha$ that is optimized during training to find the right quantization scale. The weight quantization scheme, statistics-aware weight binning (SAWB), finds the optimal scaling factor that minimizes the quantization error based on the statistical characteristics of the distribution of weights without the need for an exhaustive search. The combination of PACT and SAWB results in a 2-bit QNN that achieves state-of-the-art classification accuracy (comparable to full precision networks) across a range of popular models and datasets.

PACT: Parameterized Clipping Activation for Quantized Neural Networks

Deep learning algorithms achieve high classification accuracy at the expense of significant computation cost. To address this cost, a number of quantization schemes have been proposed - but most of these techniques focused on quantizing weights, which are relatively smaller in size compared to activations. This paper proposes a novel quantization scheme for activations during training - that enables neural networks to work well with ultra low precision weights and activations without any significant accuracy degradation. This technique, PArameterized Clipping acTivation (PACT), uses an activation clipping parameter $\alpha$ that is optimized during training to find the right quantization scale. PACT allows quantizing activations to arbitrary bit precisions, while achieving much better accuracy relative to published state-of-the-art quantization schemes. We show, for the first time, that both weights and activations can be quantized to 4-bits of precision while still achieving accuracy comparable to full precision networks across a range of popular models and datasets. We also show that exploiting these reduced-precision computational units in hardware can enable a super-linear improvement in inferencing performance due to a significant reduction in the area of accelerator compute engines coupled with the ability to retain the quantized model and activation data in on-chip memories.

AdaComp : Adaptive Residual Gradient Compression for Data-Parallel Distributed Training

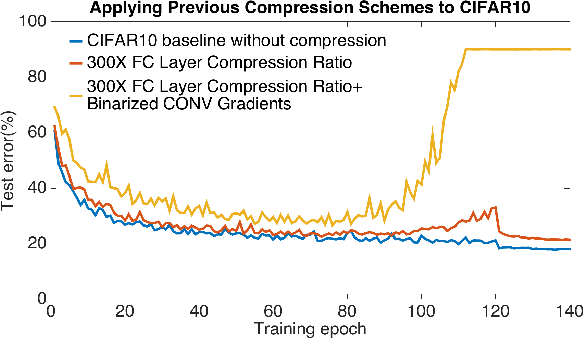
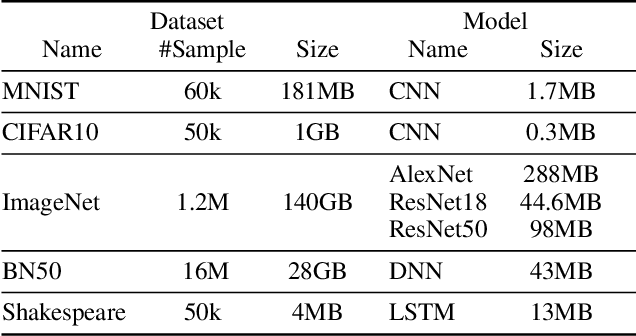
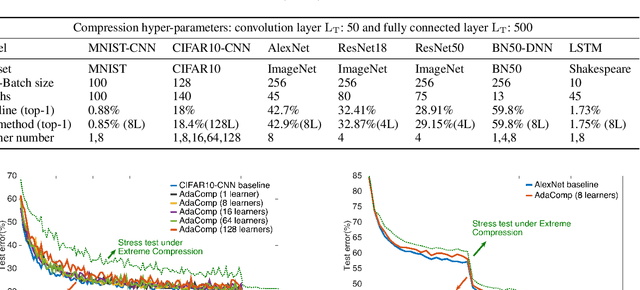
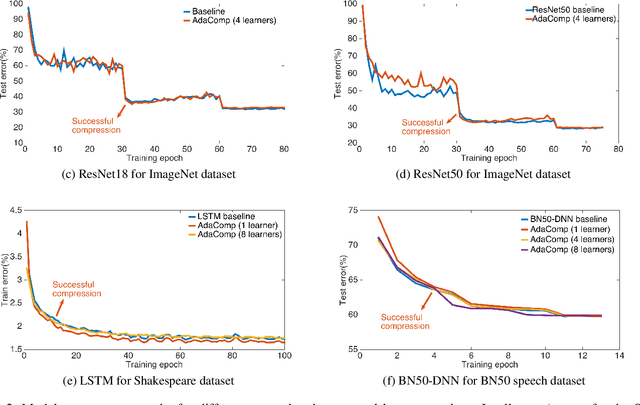
Highly distributed training of Deep Neural Networks (DNNs) on future compute platforms (offering 100 of TeraOps/s of computational capacity) is expected to be severely communication constrained. To overcome this limitation, new gradient compression techniques are needed that are computationally friendly, applicable to a wide variety of layers seen in Deep Neural Networks and adaptable to variations in network architectures as well as their hyper-parameters. In this paper we introduce a novel technique - the Adaptive Residual Gradient Compression (AdaComp) scheme. AdaComp is based on localized selection of gradient residues and automatically tunes the compression rate depending on local activity. We show excellent results on a wide spectrum of state of the art Deep Learning models in multiple domains (vision, speech, language), datasets (MNIST, CIFAR10, ImageNet, BN50, Shakespeare), optimizers (SGD with momentum, Adam) and network parameters (number of learners, minibatch-size etc.). Exploiting both sparsity and quantization, we demonstrate end-to-end compression rates of ~200X for fully-connected and recurrent layers, and ~40X for convolutional layers, without any noticeable degradation in model accuracies.

Deep Learning with Limited Numerical Precision

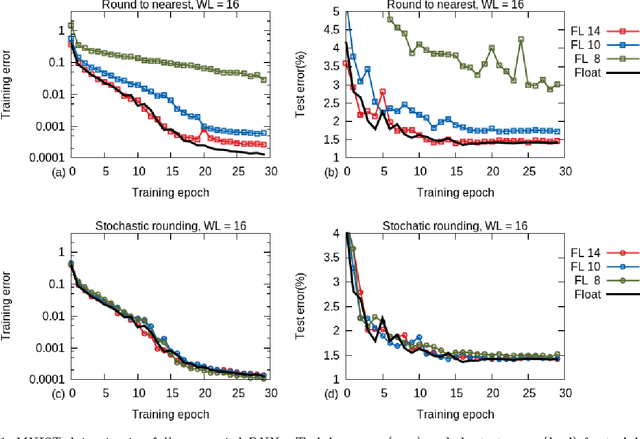
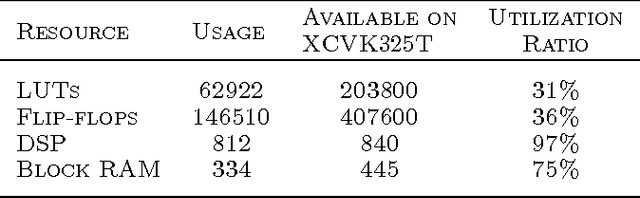
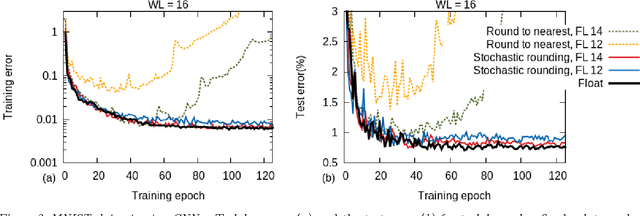
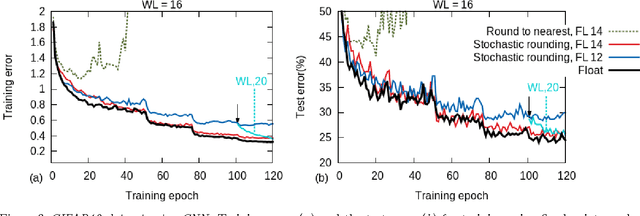
Training of large-scale deep neural networks is often constrained by the available computational resources. We study the effect of limited precision data representation and computation on neural network training. Within the context of low-precision fixed-point computations, we observe the rounding scheme to play a crucial role in determining the network's behavior during training. Our results show that deep networks can be trained using only 16-bit wide fixed-point number representation when using stochastic rounding, and incur little to no degradation in the classification accuracy. We also demonstrate an energy-efficient hardware accelerator that implements low-precision fixed-point arithmetic with stochastic rounding.