Mauricio Serrano
Accelerating Inference and Language Model Fusion of Recurrent Neural Network Transducers via End-to-End 4-bit Quantization
Jun 16, 2022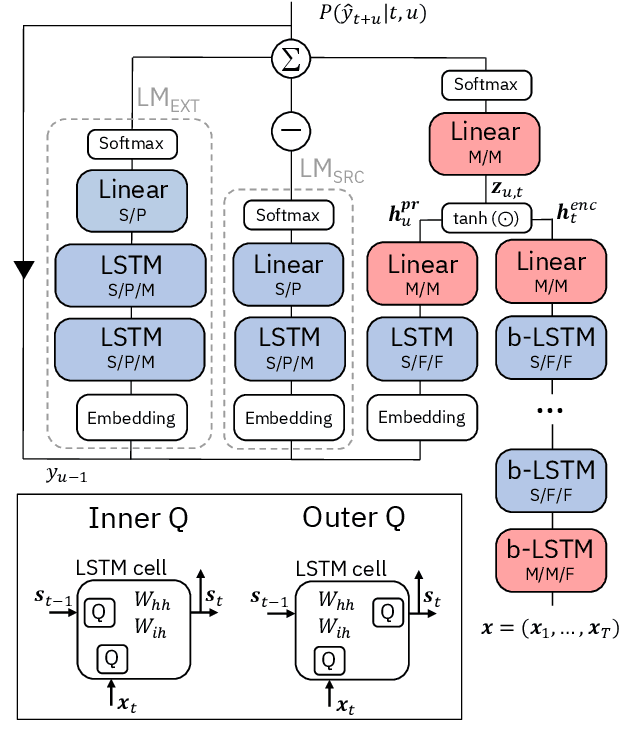
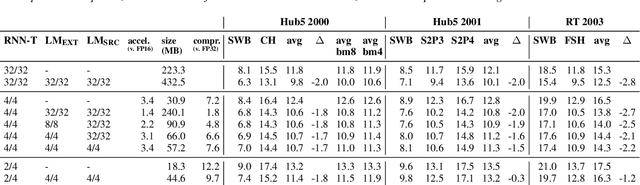
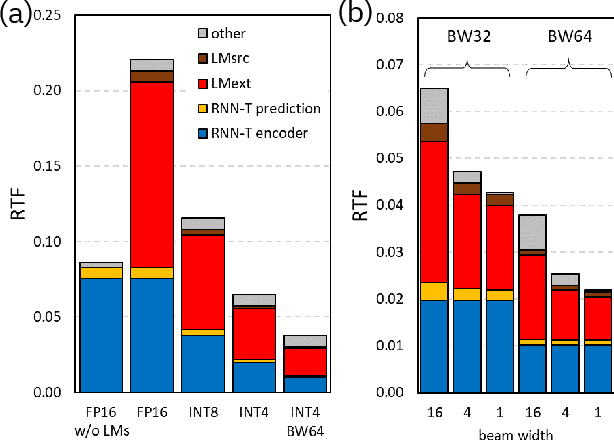
Abstract:We report on aggressive quantization strategies that greatly accelerate inference of Recurrent Neural Network Transducers (RNN-T). We use a 4 bit integer representation for both weights and activations and apply Quantization Aware Training (QAT) to retrain the full model (acoustic encoder and language model) and achieve near-iso-accuracy. We show that customized quantization schemes that are tailored to the local properties of the network are essential to achieve good performance while limiting the computational overhead of QAT. Density ratio Language Model fusion has shown remarkable accuracy gains on RNN-T workloads but it severely increases the computational cost of inference. We show that our quantization strategies enable using large beam widths for hypothesis search while achieving streaming-compatible runtimes and a full model compression ratio of 7.6$\times$ compared to the full precision model. Via hardware simulations, we estimate a 3.4$\times$ acceleration from FP16 to INT4 for the end-to-end quantized RNN-T inclusive of LM fusion, resulting in a Real Time Factor (RTF) of 0.06. On the NIST Hub5 2000, Hub5 2001, and RT-03 test sets, we retain most of the gains associated with LM fusion, improving the average WER by $>$1.5%.
4-bit Quantization of LSTM-based Speech Recognition Models
Aug 27, 2021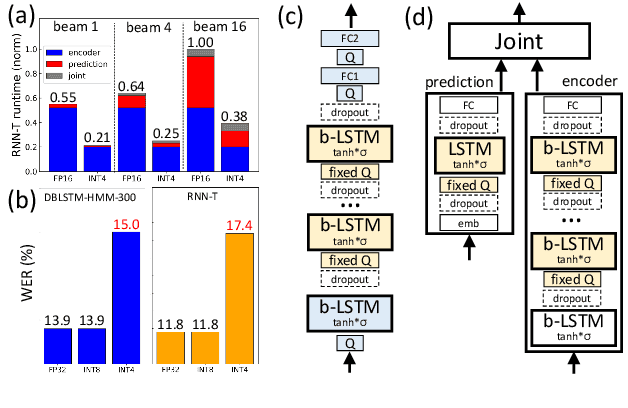
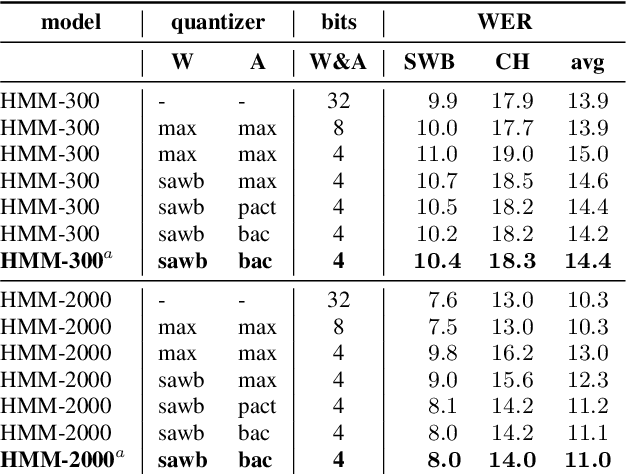
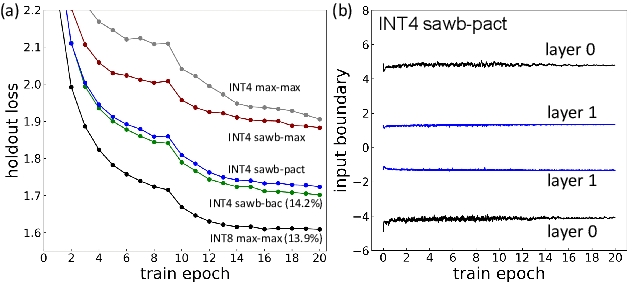
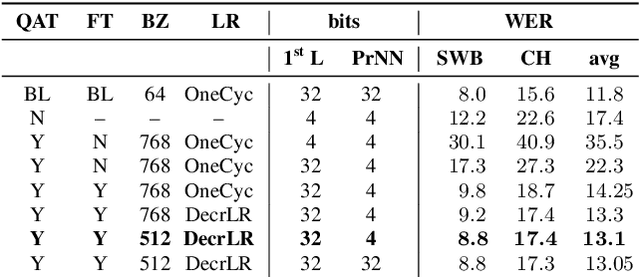
Abstract:We investigate the impact of aggressive low-precision representations of weights and activations in two families of large LSTM-based architectures for Automatic Speech Recognition (ASR): hybrid Deep Bidirectional LSTM - Hidden Markov Models (DBLSTM-HMMs) and Recurrent Neural Network - Transducers (RNN-Ts). Using a 4-bit integer representation, a na\"ive quantization approach applied to the LSTM portion of these models results in significant Word Error Rate (WER) degradation. On the other hand, we show that minimal accuracy loss is achievable with an appropriate choice of quantizers and initializations. In particular, we customize quantization schemes depending on the local properties of the network, improving recognition performance while limiting computational time. We demonstrate our solution on the Switchboard (SWB) and CallHome (CH) test sets of the NIST Hub5-2000 evaluation. DBLSTM-HMMs trained with 300 or 2000 hours of SWB data achieves $<$0.5% and $<$1% average WER degradation, respectively. On the more challenging RNN-T models, our quantization strategy limits degradation in 4-bit inference to 1.3%.
Enabling Massive Deep Neural Networks with the GraphBLAS
Aug 09, 2017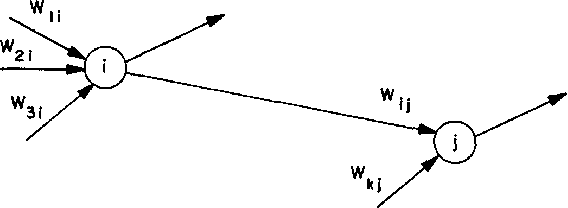
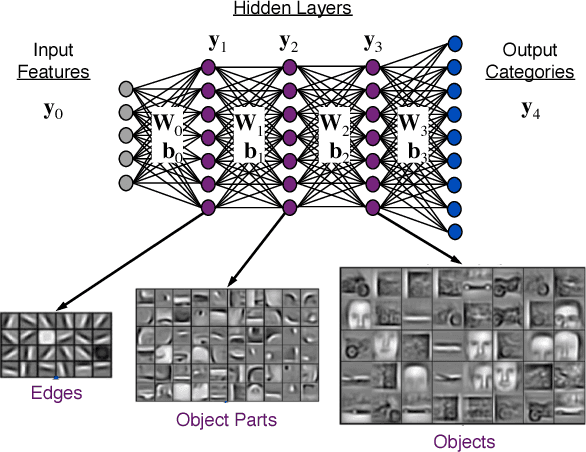
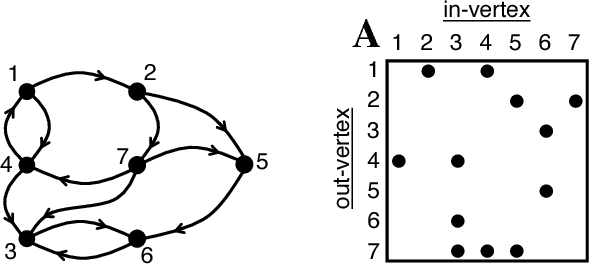

Abstract:Deep Neural Networks (DNNs) have emerged as a core tool for machine learning. The computations performed during DNN training and inference are dominated by operations on the weight matrices describing the DNN. As DNNs incorporate more stages and more nodes per stage, these weight matrices may be required to be sparse because of memory limitations. The GraphBLAS.org math library standard was developed to provide high performance manipulation of sparse weight matrices and input/output vectors. For sufficiently sparse matrices, a sparse matrix library requires significantly less memory than the corresponding dense matrix implementation. This paper provides a brief description of the mathematics underlying the GraphBLAS. In addition, the equations of a typical DNN are rewritten in a form designed to use the GraphBLAS. An implementation of the DNN is given using a preliminary GraphBLAS C library. The performance of the GraphBLAS implementation is measured relative to a standard dense linear algebra library implementation. For various sizes of DNN weight matrices, it is shown that the GraphBLAS sparse implementation outperforms a BLAS dense implementation as the weight matrix becomes sparser.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge