Advancing Direct Convolution using Convolution Slicing Optimization and ISA Extensions

Convolution is one of the most computationally intensive operations that must be performed for machine-learning model inference. A traditional approach to compute convolutions is known as the Im2Col + BLAS method. This paper proposes SConv: a direct-convolution algorithm based on a MLIR/LLVM code-generation toolchain that can be integrated into machine-learning compilers . This algorithm introduces: (a) Convolution Slicing Analysis (CSA) - a convolution-specific 3D cache-blocking analysis pass that focuses on tile reuse over the cache hierarchy; (b) Convolution Slicing Optimization (CSO) - a code-generation pass that uses CSA to generate a tiled direct-convolution macro-kernel; and (c) Vector-Based Packing (VBP) - an architecture-specific optimized input-tensor packing solution based on vector-register shift instructions for convolutions with unitary stride. Experiments conducted on 393 convolutions from full ONNX-MLIR machine-learning models indicate that the elimination of the Im2Col transformation and the use of fast packing routines result in a total packing time reduction, on full model inference, of 2.0x - 3.9x on Intel x86 and 3.6x - 7.2x on IBM POWER10. The speed-up over an Im2Col + BLAS method based on current BLAS implementations for end-to-end machine-learning model inference is in the range of 9% - 25% for Intel x86 and 10% - 42% for IBM POWER10 architectures. The total convolution speedup for model inference is 12% - 27% on Intel x86 and 26% - 46% on IBM POWER10. SConv also outperforms BLAS GEMM, when computing pointwise convolutions, in more than 83% of the 219 tested instances.

A general framework for multi-step ahead adaptive conformal heteroscedastic time series forecasting

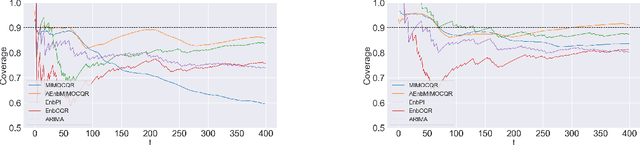
The exponential growth of machine learning (ML) has prompted a great deal of interest in quantifying the uncertainty of each prediction for a user-defined level of confidence. Reliable uncertainty quantification is crucial and is a step towards increased trust in AI results. It becomes especially important in high-stakes decision-making, where the true output must be within the confidence set with high probability. Conformal prediction (CP) is a distribution-free uncertainty quantification framework that works for any black-box model and yields prediction intervals (PIs) that are valid under the mild assumption of exchangeability. CP-type methods are gaining popularity due to being easy to implement and computationally cheap; however, the exchangeability assumption immediately excludes time series forecasting. Although recent papers tackle covariate shift, this is not enough for the general time series forecasting problem of producing H-step ahead valid PIs. To attain such a goal, we propose a new method called AEnbMIMOCQR (Adaptive ensemble batch multiinput multi-output conformalized quantile regression), which produces asymptotic valid PIs and is appropriate for heteroscedastic time series. We compare the proposed method against state-of-the-art competitive methods in the NN5 forecasting competition dataset. All the code and data to reproduce the experiments are made available

Improved conformalized quantile regression

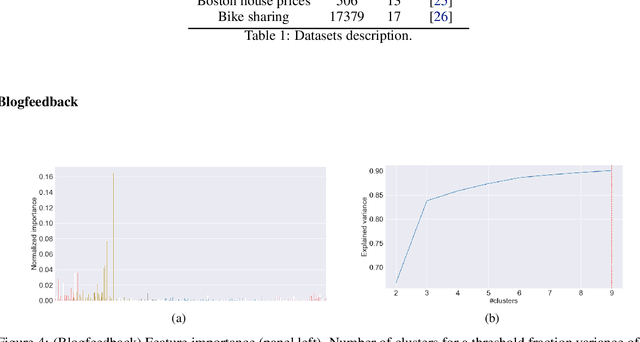
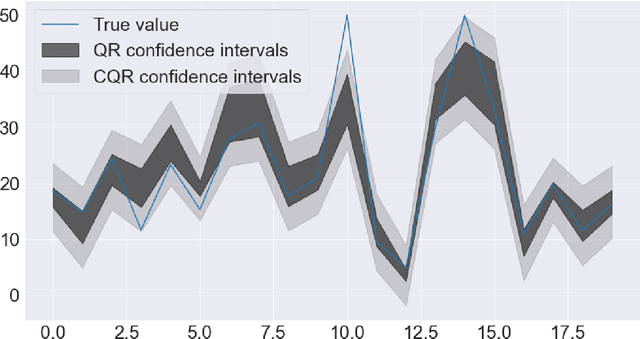
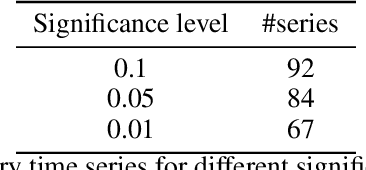
Conformalized quantile regression is a procedure that inherits the advantages of conformal prediction and quantile regression. That is, we use quantile regression to estimate the true conditional quantile and then apply a conformal step on a calibration set to ensure marginal coverage. In this way, we get adaptive prediction intervals that account for heteroscedasticity. However, the aforementioned conformal step lacks adaptiveness as described in (Romano et al., 2019). To overcome this limitation, instead of applying a single conformal step after estimating conditional quantiles with quantile regression, we propose to cluster the explanatory variables weighted by their permutation importance with an optimized k-means and apply k conformal steps. To show that this improved version outperforms the classic version of conformalized quantile regression and is more adaptive to heteroscedasticity, we extensively compare the prediction intervals of both in open datasets.

Enabling Massive Deep Neural Networks with the GraphBLAS

Deep Neural Networks (DNNs) have emerged as a core tool for machine learning. The computations performed during DNN training and inference are dominated by operations on the weight matrices describing the DNN. As DNNs incorporate more stages and more nodes per stage, these weight matrices may be required to be sparse because of memory limitations. The GraphBLAS.org math library standard was developed to provide high performance manipulation of sparse weight matrices and input/output vectors. For sufficiently sparse matrices, a sparse matrix library requires significantly less memory than the corresponding dense matrix implementation. This paper provides a brief description of the mathematics underlying the GraphBLAS. In addition, the equations of a typical DNN are rewritten in a form designed to use the GraphBLAS. An implementation of the DNN is given using a preliminary GraphBLAS C library. The performance of the GraphBLAS implementation is measured relative to a standard dense linear algebra library implementation. For various sizes of DNN weight matrices, it is shown that the GraphBLAS sparse implementation outperforms a BLAS dense implementation as the weight matrix becomes sparser.