A general framework for multi-step ahead adaptive conformal heteroscedastic time series forecasting

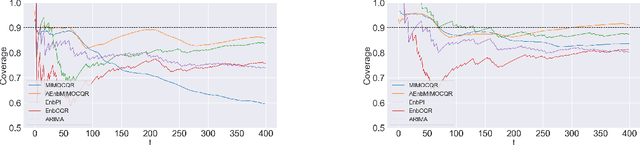
The exponential growth of machine learning (ML) has prompted a great deal of interest in quantifying the uncertainty of each prediction for a user-defined level of confidence. Reliable uncertainty quantification is crucial and is a step towards increased trust in AI results. It becomes especially important in high-stakes decision-making, where the true output must be within the confidence set with high probability. Conformal prediction (CP) is a distribution-free uncertainty quantification framework that works for any black-box model and yields prediction intervals (PIs) that are valid under the mild assumption of exchangeability. CP-type methods are gaining popularity due to being easy to implement and computationally cheap; however, the exchangeability assumption immediately excludes time series forecasting. Although recent papers tackle covariate shift, this is not enough for the general time series forecasting problem of producing H-step ahead valid PIs. To attain such a goal, we propose a new method called AEnbMIMOCQR (Adaptive ensemble batch multiinput multi-output conformalized quantile regression), which produces asymptotic valid PIs and is appropriate for heteroscedastic time series. We compare the proposed method against state-of-the-art competitive methods in the NN5 forecasting competition dataset. All the code and data to reproduce the experiments are made available

Improved conformalized quantile regression

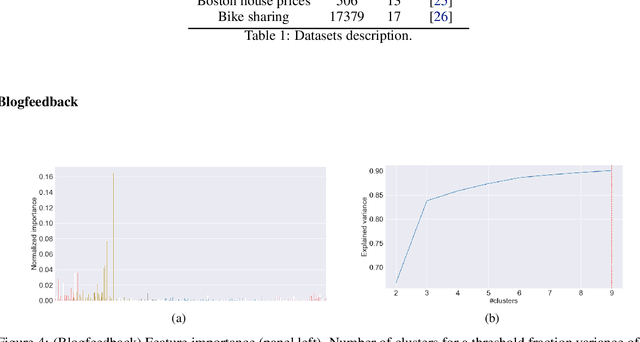
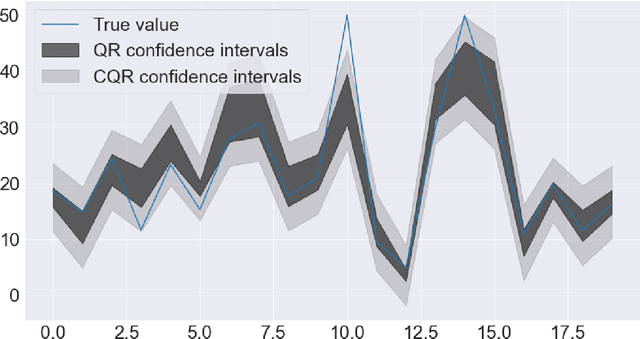
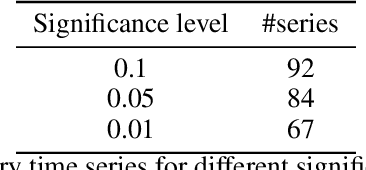
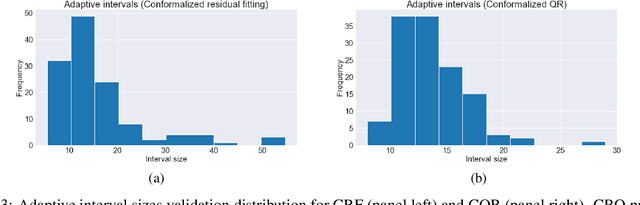
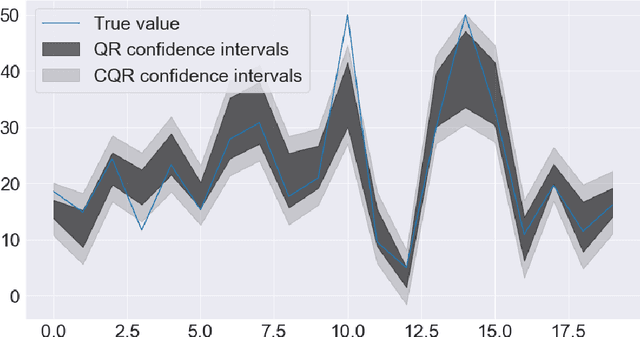
Conformalized quantile regression is a procedure that inherits the advantages of conformal prediction and quantile regression. That is, we use quantile regression to estimate the true conditional quantile and then apply a conformal step on a calibration set to ensure marginal coverage. In this way, we get adaptive prediction intervals that account for heteroscedasticity. However, the aforementioned conformal step lacks adaptiveness as described in (Romano et al., 2019). To overcome this limitation, instead of applying a single conformal step after estimating conditional quantiles with quantile regression, we propose to cluster the explanatory variables weighted by their permutation importance with an optimized k-means and apply k conformal steps. To show that this improved version outperforms the classic version of conformalized quantile regression and is more adaptive to heteroscedasticity, we extensively compare the prediction intervals of both in open datasets.

Inductive Conformal Prediction: A Straightforward Introduction with Examples in Python

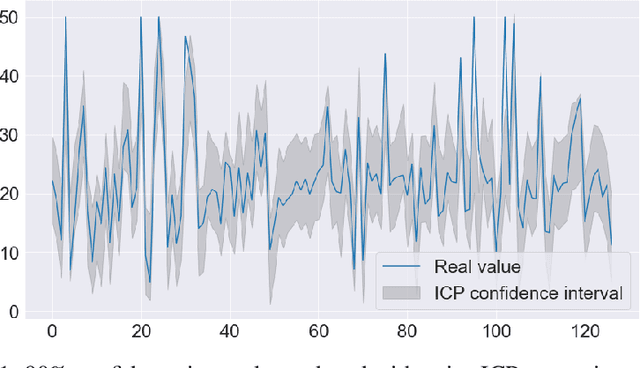
Inductive Conformal Prediction (ICP) is a set of distribution-free and model agnostic algorithms devised to predict with a user-defined confidence with coverage guarantee. Instead of having point predictions, i.e., a real number in the case of regression or a single class in multi class classification, models calibrated using ICP output an interval or a set of classes, respectively. ICP takes special importance in high-risk settings where we want the true output to belong to the prediction set with high probability. As an example, a classification model might output that given a magnetic resonance image a patient has no latent diseases to report. However, this model output was based on the most likely class, the second most likely class might tell that the patient has a 15% chance of brain tumor or other severe disease and therefore further exams should be conducted. Using ICP is therefore way more informative and we believe that should be the standard way of producing forecasts. This paper is a hands-on introduction, this means that we will provide examples as we introduce the theory.