Optimal Clipping and Magnitude-aware Differentiation for Improved Quantization-aware Training

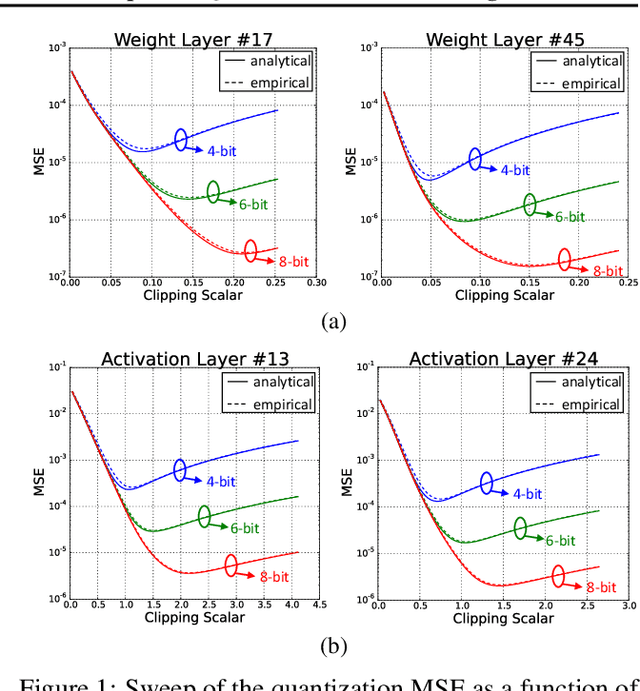
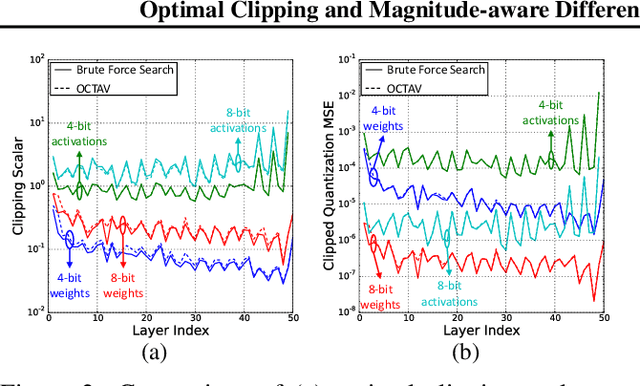
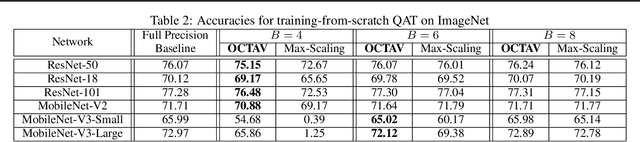
Data clipping is crucial in reducing noise in quantization operations and improving the achievable accuracy of quantization-aware training (QAT). Current practices rely on heuristics to set clipping threshold scalars and cannot be shown to be optimal. We propose Optimally Clipped Tensors And Vectors (OCTAV), a recursive algorithm to determine MSE-optimal clipping scalars. Derived from the fast Newton-Raphson method, OCTAV finds optimal clipping scalars on the fly, for every tensor, at every iteration of the QAT routine. Thus, the QAT algorithm is formulated with provably minimum quantization noise at each step. In addition, we reveal limitations in common gradient estimation techniques in QAT and propose magnitude-aware differentiation as a remedy to further improve accuracy. Experimentally, OCTAV-enabled QAT achieves state-of-the-art accuracy on multiple tasks. These include training-from-scratch and retraining ResNets and MobileNets on ImageNet, and Squad fine-tuning using BERT models, where OCTAV-enabled QAT consistently preserves accuracy at low precision (4-to-6-bits). Our results require no modifications to the baseline training recipe, except for the insertion of quantization operations where appropriate.

Low-Precision Training in Logarithmic Number System using Multiplicative Weight Update

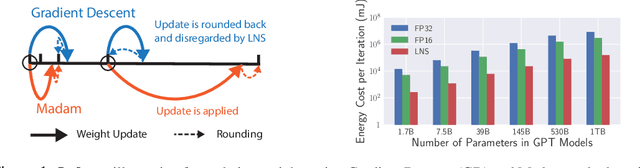
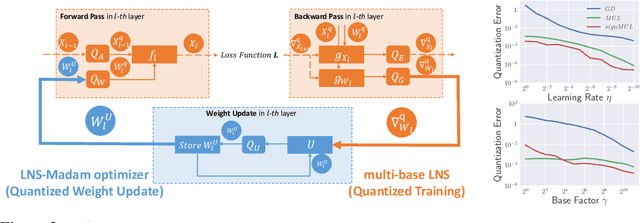
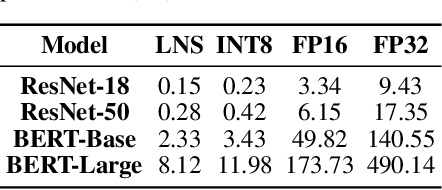
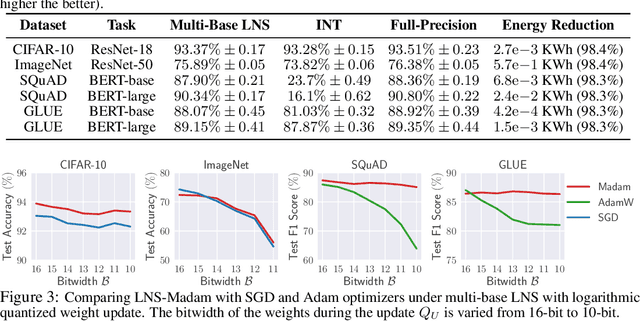
Training large-scale deep neural networks (DNNs) currently requires a significant amount of energy, leading to serious environmental impacts. One promising approach to reduce the energy costs is representing DNNs with low-precision numbers. While it is common to train DNNs with forward and backward propagation in low-precision, training directly over low-precision weights, without keeping a copy of weights in high-precision, still remains to be an unsolved problem. This is due to complex interactions between learning algorithms and low-precision number systems. To address this, we jointly design a low-precision training framework involving a logarithmic number system (LNS) and a multiplicative weight update training method, termed LNS-Madam. LNS has a high dynamic range even in a low-bitwidth setting, leading to high energy efficiency and making it relevant for on-board training in energy-constrained edge devices. We design LNS to have the flexibility of choosing different bases for weights and gradients, as they usually require different quantization gaps and dynamic ranges during training. By drawing the connection between LNS and multiplicative update, LNS-Madam ensures low quantization error during weight update, leading to a stable convergence even if the bitwidth is limited. Compared to using a fixed-point or floating-point number system and training with popular learning algorithms such as SGD and Adam, our joint design with LNS and LNS-Madam optimizer achieves better accuracy while requiring smaller bitwidth. Notably, with only 5-bit for gradients, the proposed training framework achieves accuracy comparable to full-precision state-of-the-art models such as ResNet-50 and BERT. After conducting energy estimations by analyzing the math datapath units during training, the results show that our design achieves over 60x energy reduction compared to FP32 on BERT models.

VS-Quant: Per-vector Scaled Quantization for Accurate Low-Precision Neural Network Inference

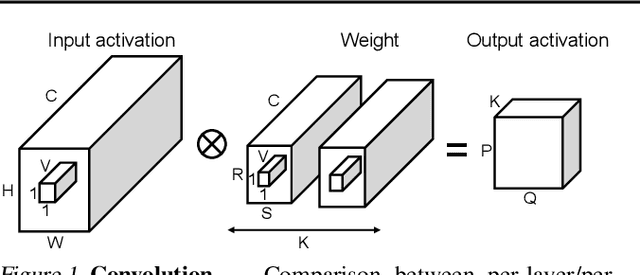
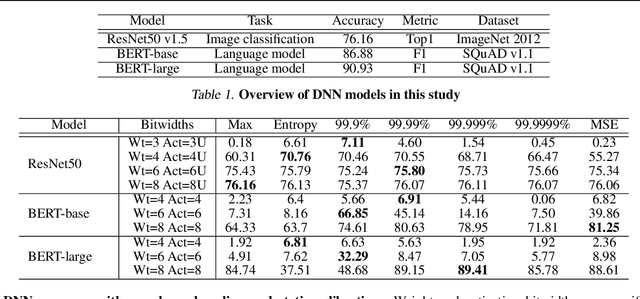
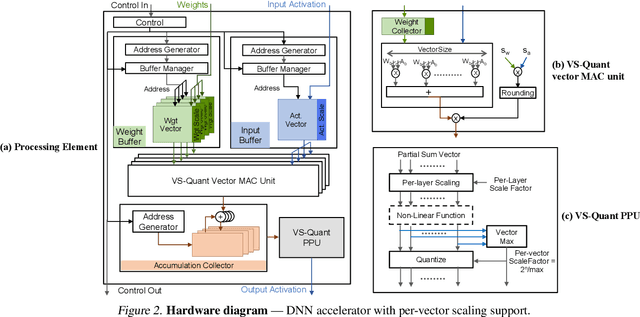
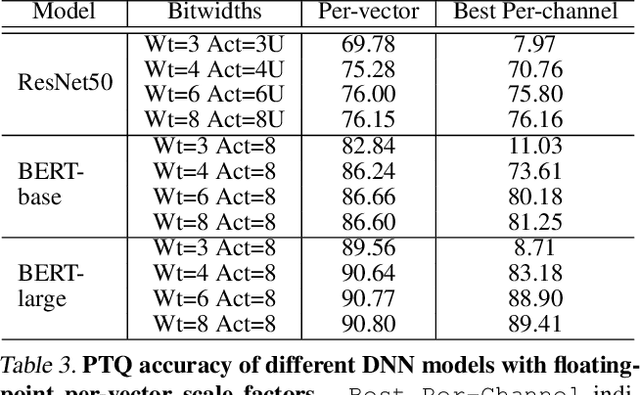
Quantization enables efficient acceleration of deep neural networks by reducing model memory footprint and exploiting low-cost integer math hardware units. Quantization maps floating-point weights and activations in a trained model to low-bitwidth integer values using scale factors. Excessive quantization, reducing precision too aggressively, results in accuracy degradation. When scale factors are shared at a coarse granularity across many dimensions of each tensor, effective precision of individual elements within the tensor are limited. To reduce quantization-related accuracy loss, we propose using a separate scale factor for each small vector of ($\approx$16-64) elements within a single dimension of a tensor. To achieve an efficient hardware implementation, the per-vector scale factors can be implemented with low-bitwidth integers when calibrated using a two-level quantization scheme. We find that per-vector scaling consistently achieves better inference accuracy at low precision compared to conventional scaling techniques for popular neural networks without requiring retraining. We also modify a deep learning accelerator hardware design to study the area and energy overheads of per-vector scaling support. Our evaluation demonstrates that per-vector scaled quantization with 4-bit weights and activations achieves 37% area saving and 24% energy saving while maintaining over 75% accuracy for ResNet50 on ImageNet. 4-bit weights and 8-bit activations achieve near-full-precision accuracy for both BERT-base and BERT-large on SQuAD while reducing area by 26% compared to an 8-bit baseline.