Optimal Clipping and Magnitude-aware Differentiation for Improved Quantization-aware Training
Paper and Code
Jun 13, 2022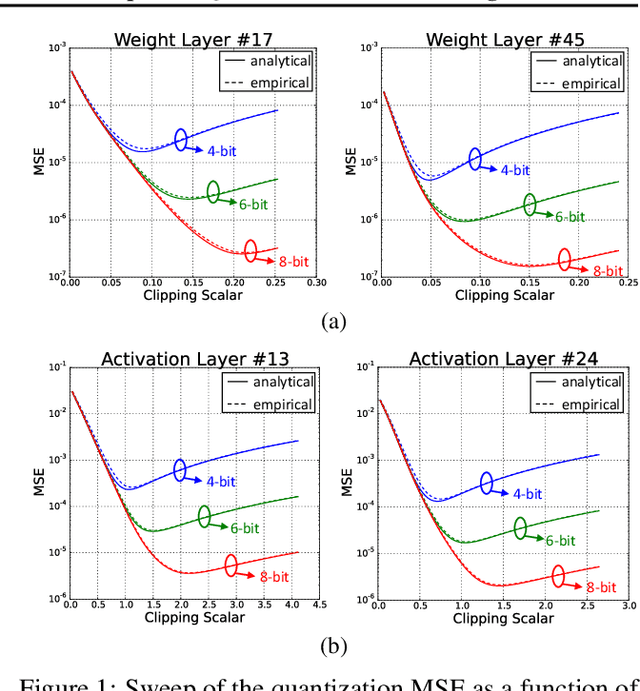

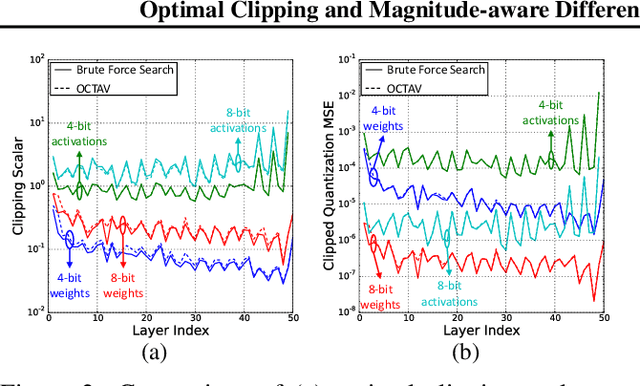
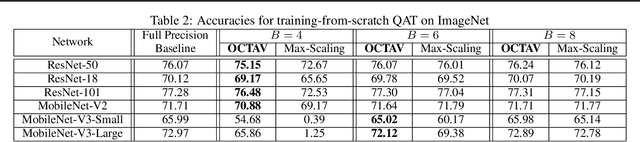
Data clipping is crucial in reducing noise in quantization operations and improving the achievable accuracy of quantization-aware training (QAT). Current practices rely on heuristics to set clipping threshold scalars and cannot be shown to be optimal. We propose Optimally Clipped Tensors And Vectors (OCTAV), a recursive algorithm to determine MSE-optimal clipping scalars. Derived from the fast Newton-Raphson method, OCTAV finds optimal clipping scalars on the fly, for every tensor, at every iteration of the QAT routine. Thus, the QAT algorithm is formulated with provably minimum quantization noise at each step. In addition, we reveal limitations in common gradient estimation techniques in QAT and propose magnitude-aware differentiation as a remedy to further improve accuracy. Experimentally, OCTAV-enabled QAT achieves state-of-the-art accuracy on multiple tasks. These include training-from-scratch and retraining ResNets and MobileNets on ImageNet, and Squad fine-tuning using BERT models, where OCTAV-enabled QAT consistently preserves accuracy at low precision (4-to-6-bits). Our results require no modifications to the baseline training recipe, except for the insertion of quantization operations where appropriate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge