BCQ: Block Clustered Quantization for 4-bit (W4A4) LLM Inference

Post-training quantization (PTQ) is a promising approach to reducing the storage and computational requirements of large language models (LLMs) without additional training cost. Recent PTQ studies have primarily focused on quantizing only weights to sub-8-bits while maintaining activations at 8-bits or higher. Accurate sub-8-bit quantization for both weights and activations without relying on quantization-aware training remains a significant challenge. We propose a novel quantization method called block clustered quantization (BCQ) wherein each operand tensor is decomposed into blocks (a block is a group of contiguous scalars), blocks are clustered based on their statistics, and a dedicated optimal quantization codebook is designed for each cluster. As a specific embodiment of this approach, we propose a PTQ algorithm called Locally-Optimal BCQ (LO-BCQ) that iterates between the steps of block clustering and codebook design to greedily minimize the quantization mean squared error. When weight and activation scalars are encoded to W4A4 format (with 0.5-bits of overhead for storing scaling factors and codebook selectors), we advance the current state-of-the-art by demonstrating <1% loss in inference accuracy across several LLMs and downstream tasks.

Ax-BxP: Approximate Blocked Computation for Precision-Reconfigurable Deep Neural Network Acceleration

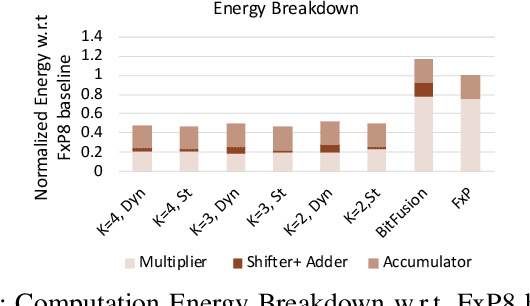
Precision scaling has emerged as a popular technique to optimize the compute and storage requirements of Deep Neural Networks (DNNs). Efforts toward creating ultra-low-precision (sub-8-bit) DNNs suggest that the minimum precision required to achieve a given network-level accuracy varies considerably across networks, and even across layers within a network, requiring support for variable precision in DNN hardware. Previous proposals such as bit-serial hardware incur high overheads, significantly diminishing the benefits of lower precision. To efficiently support precision re-configurability in DNN accelerators, we introduce an approximate computing method wherein DNN computations are performed block-wise (a block is a group of bits) and re-configurability is supported at the granularity of blocks. Results of block-wise computations are composed in an approximate manner to enable efficient re-configurability. We design a DNN accelerator that embodies approximate blocked computation and propose a method to determine a suitable approximation configuration for a given DNN. By varying the approximation configurations across DNNs, we achieve 1.11x-1.34x and 1.29x-1.6x improvement in system energy and performance respectively, over an 8-bit fixed-point (FxP8) baseline, with negligible loss in classification accuracy. Further, by varying the approximation configurations across layers and data-structures within DNNs, we achieve 1.14x-1.67x and 1.31x-1.93x improvement in system energy and performance respectively, with negligible accuracy loss.