DeepSeek-Prover-V1.5: Harnessing Proof Assistant Feedback for Reinforcement Learning and Monte-Carlo Tree Search

We introduce DeepSeek-Prover-V1.5, an open-source language model designed for theorem proving in Lean 4, which enhances DeepSeek-Prover-V1 by optimizing both training and inference processes. Pre-trained on DeepSeekMath-Base with specialization in formal mathematical languages, the model undergoes supervised fine-tuning using an enhanced formal theorem proving dataset derived from DeepSeek-Prover-V1. Further refinement is achieved through reinforcement learning from proof assistant feedback (RLPAF). Beyond the single-pass whole-proof generation approach of DeepSeek-Prover-V1, we propose RMaxTS, a variant of Monte-Carlo tree search that employs an intrinsic-reward-driven exploration strategy to generate diverse proof paths. DeepSeek-Prover-V1.5 demonstrates significant improvements over DeepSeek-Prover-V1, achieving new state-of-the-art results on the test set of the high school level miniF2F benchmark ($63.5\%$) and the undergraduate level ProofNet benchmark ($25.3\%$).

DeepSeek-Coder-V2: Breaking the Barrier of Closed-Source Models in Code Intelligence

We present DeepSeek-Coder-V2, an open-source Mixture-of-Experts (MoE) code language model that achieves performance comparable to GPT4-Turbo in code-specific tasks. Specifically, DeepSeek-Coder-V2 is further pre-trained from an intermediate checkpoint of DeepSeek-V2 with additional 6 trillion tokens. Through this continued pre-training, DeepSeek-Coder-V2 substantially enhances the coding and mathematical reasoning capabilities of DeepSeek-V2, while maintaining comparable performance in general language tasks. Compared to DeepSeek-Coder-33B, DeepSeek-Coder-V2 demonstrates significant advancements in various aspects of code-related tasks, as well as reasoning and general capabilities. Additionally, DeepSeek-Coder-V2 expands its support for programming languages from 86 to 338, while extending the context length from 16K to 128K. In standard benchmark evaluations, DeepSeek-Coder-V2 achieves superior performance compared to closed-source models such as GPT4-Turbo, Claude 3 Opus, and Gemini 1.5 Pro in coding and math benchmarks.

Rho-1: Not All Tokens Are What You Need

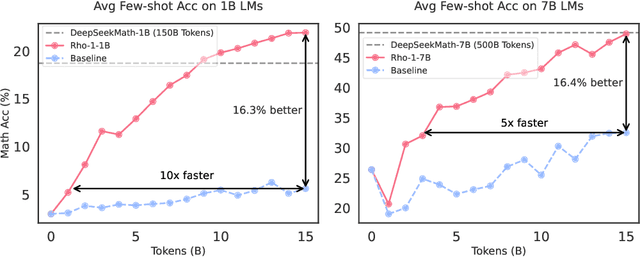
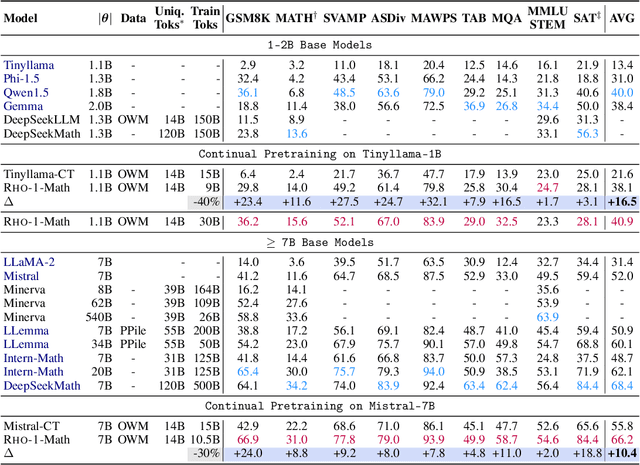
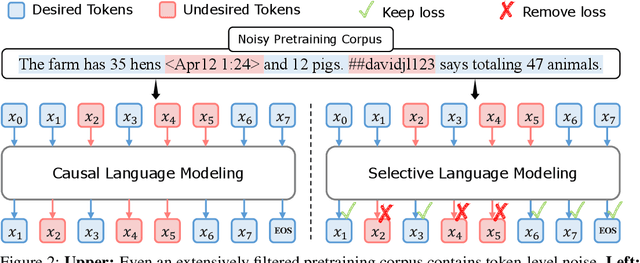
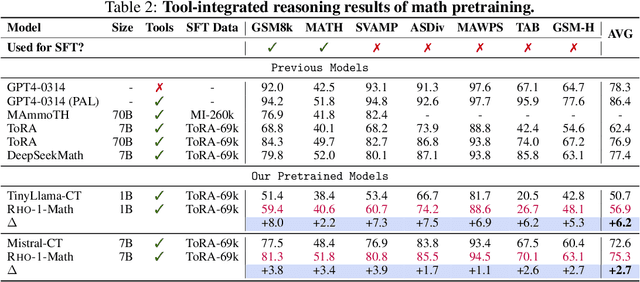
Previous language model pre-training methods have uniformly applied a next-token prediction loss to all training tokens. Challenging this norm, we posit that "Not all tokens in a corpus are equally important for language model training". Our initial analysis delves into token-level training dynamics of language model, revealing distinct loss patterns for different tokens. Leveraging these insights, we introduce a new language model called Rho-1. Unlike traditional LMs that learn to predict every next token in a corpus, Rho-1 employs Selective Language Modeling (SLM), which selectively trains on useful tokens that aligned with the desired distribution. This approach involves scoring pretraining tokens using a reference model, and then training the language model with a focused loss on tokens with higher excess loss. When continual pretraining on 15B OpenWebMath corpus, Rho-1 yields an absolute improvement in few-shot accuracy of up to 30% in 9 math tasks. After fine-tuning, Rho-1-1B and 7B achieved state-of-the-art results of 40.6% and 51.8% on MATH dataset, respectively - matching DeepSeekMath with only 3% of the pretraining tokens. Furthermore, when pretraining on 80B general tokens, Rho-1 achieves 6.8% average enhancement across 15 diverse tasks, increasing both efficiency and performance of the language model pre-training.

Exploring the Mystery of Influential Data for Mathematical Reasoning

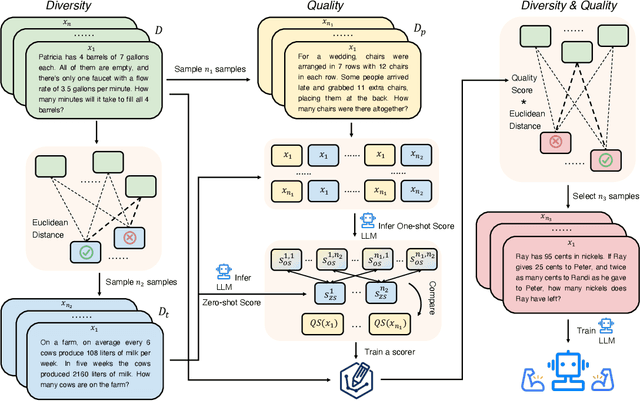
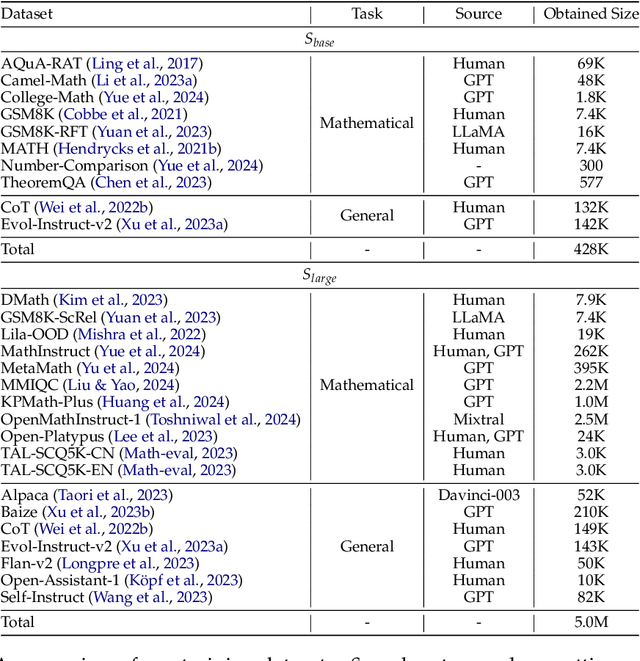
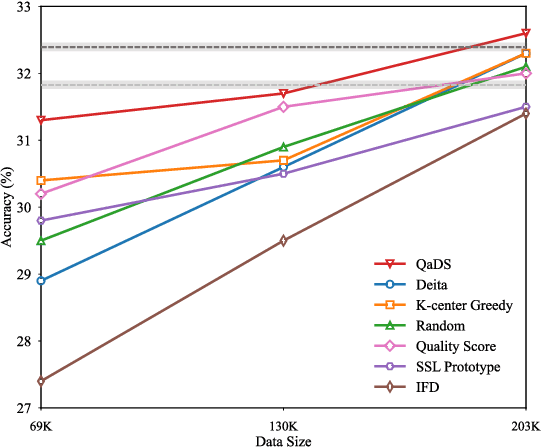
Selecting influential data for fine-tuning on downstream tasks is a key factor for both performance and computation efficiency. Recent works have shown that training with only limited data can show a superior performance on general tasks. However, the feasibility on mathematical reasoning tasks has not been validated. To go further, there exist two open questions for mathematical reasoning: how to select influential data and what is an influential data composition. For the former one, we propose a Quality-aware Diverse Selection (QaDS) strategy adaptable for mathematical reasoning. A comparison with other selection strategies validates the superiority of QaDS. For the latter one, we first enlarge our setting and explore the influential data composition. We conduct a series of experiments and highlight: scaling up reasoning data, and training with general data selected by QaDS is helpful. Then, we define our optimal mixture as OpenMathMix, an influential data mixture with open-source data selected by QaDS. With OpenMathMix, we achieve a state-of-the-art 48.8% accuracy on MATH with 7B base model. Additionally, we showcase the use of QaDS in creating efficient fine-tuning mixtures with various selection ratios, and analyze the quality of a wide range of open-source datasets, which can perform as a reference for future works on mathematical reasoning tasks.

CriticBench: Benchmarking LLMs for Critique-Correct Reasoning

The ability of Large Language Models (LLMs) to critique and refine their reasoning is crucial for their application in evaluation, feedback provision, and self-improvement. This paper introduces CriticBench, a comprehensive benchmark designed to assess LLMs' abilities to critique and rectify their reasoning across a variety of tasks. CriticBench encompasses five reasoning domains: mathematical, commonsense, symbolic, coding, and algorithmic. It compiles 15 datasets and incorporates responses from three LLM families. Utilizing CriticBench, we evaluate and dissect the performance of 17 LLMs in generation, critique, and correction reasoning, i.e., GQC reasoning. Our findings reveal: (1) a linear relationship in GQC capabilities, with critique-focused training markedly enhancing performance; (2) a task-dependent variation in correction effectiveness, with logic-oriented tasks being more amenable to correction; (3) GQC knowledge inconsistencies that decrease as model size increases; and (4) an intriguing inter-model critiquing dynamic, where stronger models are better at critiquing weaker ones, while weaker models can surprisingly surpass stronger ones in their self-critique. We hope these insights into the nuanced critique-correct reasoning of LLMs will foster further research in LLM critique and self-improvement.

Key-Point-Driven Data Synthesis with its Enhancement on Mathematical Reasoning

Large language models (LLMs) have shown great potential in complex reasoning tasks, yet their performance is often hampered by the scarcity of high-quality, reasoning-focused training datasets. Addressing this challenge, we propose Key-Point-Driven Data Synthesis (KPDDS), a novel data synthesis framework that synthesizes question-answer pairs by leveraging key points and exemplar pairs from authentic data sources. KPDDS ensures the generation of novel questions with rigorous quality control and substantial scalability. As a result, we present KPMath, the most extensive synthetic dataset tailored for mathematical reasoning to date, comprising over one million question-answer pairs. Utilizing KPMath and augmenting it with additional reasoning-intensive corpora, we create the comprehensive KPMath-Plus dataset. Fine-tuning the Mistral-7B model on KPMath-Plus yields a zero-shot PASS@1 accuracy of 39.3% on the MATH test set, a performance that not only outpaces other finetuned 7B models but also exceeds that of certain 34B models. Our ablation studies further confirm the substantial enhancement in mathematical reasoning across various subtopics, marking a significant stride in LLMs' reasoning capabilities.

SciAgent: Tool-augmented Language Models for Scientific Reasoning

Scientific reasoning poses an excessive challenge for even the most advanced Large Language Models (LLMs). To make this task more practical and solvable for LLMs, we introduce a new task setting named tool-augmented scientific reasoning. This setting supplements LLMs with scalable toolsets, and shifts the focus from pursuing an omniscient problem solver to a proficient tool-user. To facilitate the research of such setting, we construct a tool-augmented training corpus named MathFunc which encompasses over 30,000 samples and roughly 6,000 tools. Building on MathFunc, we develop SciAgent to retrieve, understand and, if necessary, use tools for scientific problem solving. Additionally, we craft a benchmark, SciToolBench, spanning five scientific domains to evaluate LLMs' abilities with tool assistance. Extensive experiments on SciToolBench confirm the effectiveness of SciAgent. Notably, SciAgent-Mistral-7B surpasses other LLMs with the same size by more than 13% in absolute accuracy. Furthermore, SciAgent-DeepMath-7B shows much superior performance than ChatGPT.

ToRA: A Tool-Integrated Reasoning Agent for Mathematical Problem Solving

Large language models have made significant progress in various language tasks, yet they still struggle with complex mathematics. In this paper, we propose ToRA a series of Tool-integrated Reasoning Agents designed to solve challenging mathematical problems by seamlessly integrating natural language reasoning with the utilization of external tools (e.g., computation libraries and symbolic solvers), thereby amalgamating the analytical prowess of language and the computational efficiency of tools. To train ToRA, we curate interactive tool-use trajectories on mathematical datasets, apply imitation learning on the annotations, and propose output space shaping to further refine models' reasoning behavior. As a result, ToRA models significantly outperform open-source models on 10 mathematical reasoning datasets across all scales with 13%-19% absolute improvements on average. Notably, ToRA-7B reaches 44.6% on the competition-level dataset MATH, surpassing the best open-source model WizardMath-70B by 22% absolute. ToRA-Code-34B is also the first open-source model that achieves an accuracy exceeding 50% on MATH, which significantly outperforms GPT-4's CoT result, and is competitive with GPT-4 solving problems with programs. Additionally, we conduct a comprehensive analysis of the benefits and remaining challenges of tool interaction for mathematical reasoning, providing valuable insights for future research.

MvP: Multi-view Prompting Improves Aspect Sentiment Tuple Prediction

Generative methods greatly promote aspect-based sentiment analysis via generating a sequence of sentiment elements in a specified format. However, existing studies usually predict sentiment elements in a fixed order, which ignores the effect of the interdependence of the elements in a sentiment tuple and the diversity of language expression on the results. In this work, we propose Multi-view Prompting (MvP) that aggregates sentiment elements generated in different orders, leveraging the intuition of human-like problem-solving processes from different views. Specifically, MvP introduces element order prompts to guide the language model to generate multiple sentiment tuples, each with a different element order, and then selects the most reasonable tuples by voting. MvP can naturally model multi-view and multi-task as permutations and combinations of elements, respectively, outperforming previous task-specific designed methods on multiple ABSA tasks with a single model. Extensive experiments show that MvP significantly advances the state-of-the-art performance on 10 datasets of 4 benchmark tasks, and performs quite effectively in low-resource settings. Detailed evaluation verified the effectiveness, flexibility, and cross-task transferability of MvP.

CRITIC: Large Language Models Can Self-Correct with Tool-Interactive Critiquing

Recent developments in large language models (LLMs) have been impressive. However, these models sometimes show inconsistencies and problematic behavior, such as hallucinating facts, generating flawed code, or creating offensive and toxic content. Unlike these models, humans typically utilize external tools to cross-check and refine their initial content, like using a search engine for fact-checking, or a code interpreter for debugging. Inspired by this observation, we introduce a framework called CRITIC that allows LLMs, which are essentially "black boxes" to validate and progressively amend their own outputs in a manner similar to human interaction with tools. More specifically, starting with an initial output, CRITIC interacts with appropriate tools to evaluate certain aspects of the text, and then revises the output based on the feedback obtained during this validation process. Comprehensive evaluations involving free-form question answering, mathematical program synthesis, and toxicity reduction demonstrate that CRITIC consistently enhances the performance of LLMs. Meanwhile, our research highlights the crucial importance of external feedback in promoting the ongoing self-improvement of LLMs.