DeepSeek-Prover-V1.5: Harnessing Proof Assistant Feedback for Reinforcement Learning and Monte-Carlo Tree Search

We introduce DeepSeek-Prover-V1.5, an open-source language model designed for theorem proving in Lean 4, which enhances DeepSeek-Prover-V1 by optimizing both training and inference processes. Pre-trained on DeepSeekMath-Base with specialization in formal mathematical languages, the model undergoes supervised fine-tuning using an enhanced formal theorem proving dataset derived from DeepSeek-Prover-V1. Further refinement is achieved through reinforcement learning from proof assistant feedback (RLPAF). Beyond the single-pass whole-proof generation approach of DeepSeek-Prover-V1, we propose RMaxTS, a variant of Monte-Carlo tree search that employs an intrinsic-reward-driven exploration strategy to generate diverse proof paths. DeepSeek-Prover-V1.5 demonstrates significant improvements over DeepSeek-Prover-V1, achieving new state-of-the-art results on the test set of the high school level miniF2F benchmark ($63.5\%$) and the undergraduate level ProofNet benchmark ($25.3\%$).

DeepSeek-Coder-V2: Breaking the Barrier of Closed-Source Models in Code Intelligence

We present DeepSeek-Coder-V2, an open-source Mixture-of-Experts (MoE) code language model that achieves performance comparable to GPT4-Turbo in code-specific tasks. Specifically, DeepSeek-Coder-V2 is further pre-trained from an intermediate checkpoint of DeepSeek-V2 with additional 6 trillion tokens. Through this continued pre-training, DeepSeek-Coder-V2 substantially enhances the coding and mathematical reasoning capabilities of DeepSeek-V2, while maintaining comparable performance in general language tasks. Compared to DeepSeek-Coder-33B, DeepSeek-Coder-V2 demonstrates significant advancements in various aspects of code-related tasks, as well as reasoning and general capabilities. Additionally, DeepSeek-Coder-V2 expands its support for programming languages from 86 to 338, while extending the context length from 16K to 128K. In standard benchmark evaluations, DeepSeek-Coder-V2 achieves superior performance compared to closed-source models such as GPT4-Turbo, Claude 3 Opus, and Gemini 1.5 Pro in coding and math benchmarks.

DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

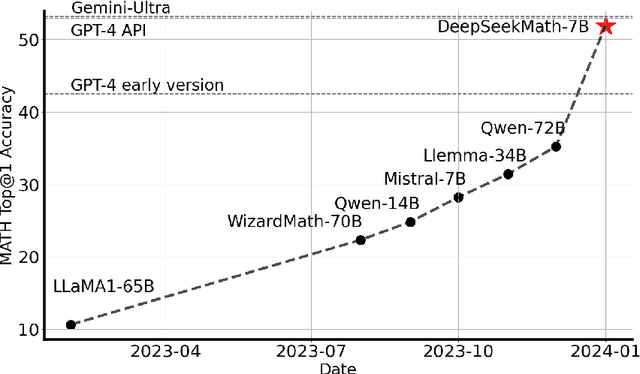
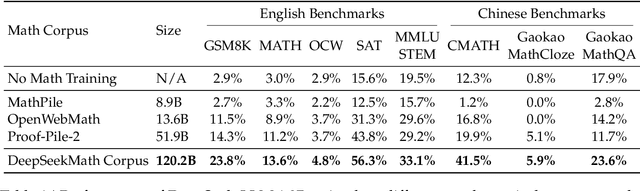
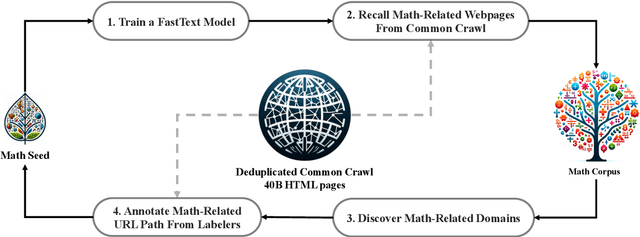
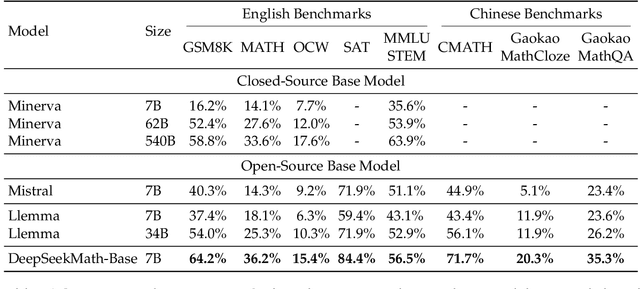
Mathematical reasoning poses a significant challenge for language models due to its complex and structured nature. In this paper, we introduce DeepSeekMath 7B, which continues pre-training DeepSeek-Coder-Base-v1.5 7B with 120B math-related tokens sourced from Common Crawl, together with natural language and code data. DeepSeekMath 7B has achieved an impressive score of 51.7% on the competition-level MATH benchmark without relying on external toolkits and voting techniques, approaching the performance level of Gemini-Ultra and GPT-4. Self-consistency over 64 samples from DeepSeekMath 7B achieves 60.9% on MATH. The mathematical reasoning capability of DeepSeekMath is attributed to two key factors: First, we harness the significant potential of publicly available web data through a meticulously engineered data selection pipeline. Second, we introduce Group Relative Policy Optimization (GRPO), a variant of Proximal Policy Optimization (PPO), that enhances mathematical reasoning abilities while concurrently optimizing the memory usage of PPO.

DeepSeek LLM: Scaling Open-Source Language Models with Longtermism

The rapid development of open-source large language models (LLMs) has been truly remarkable. However, the scaling law described in previous literature presents varying conclusions, which casts a dark cloud over scaling LLMs. We delve into the study of scaling laws and present our distinctive findings that facilitate scaling of large scale models in two commonly used open-source configurations, 7B and 67B. Guided by the scaling laws, we introduce DeepSeek LLM, a project dedicated to advancing open-source language models with a long-term perspective. To support the pre-training phase, we have developed a dataset that currently consists of 2 trillion tokens and is continuously expanding. We further conduct supervised fine-tuning (SFT) and Direct Preference Optimization (DPO) on DeepSeek LLM Base models, resulting in the creation of DeepSeek Chat models. Our evaluation results demonstrate that DeepSeek LLM 67B surpasses LLaMA-2 70B on various benchmarks, particularly in the domains of code, mathematics, and reasoning. Furthermore, open-ended evaluations reveal that DeepSeek LLM 67B Chat exhibits superior performance compared to GPT-3.5.

SCC: an efficient deep reinforcement learning agent mastering the game of StarCraft II

AlphaStar, the AI that reaches GrandMaster level in StarCraft II, is a remarkable milestone demonstrating what deep reinforcement learning can achieve in complex Real-Time Strategy (RTS) games. However, the complexities of the game, algorithms and systems, and especially the tremendous amount of computation needed are big obstacles for the community to conduct further research in this direction. We propose a deep reinforcement learning agent, StarCraft Commander (SCC). With order of magnitude less computation, it demonstrates top human performance defeating GrandMaster players in test matches and top professional players in a live event. Moreover, it shows strong robustness to various human strategies and discovers novel strategies unseen from human plays. In this paper, we will share the key insights and optimizations on efficient imitation learning and reinforcement learning for StarCraft II full game.

Sparse Generalized Eigenvalue Problem via Smooth Optimization

In this paper, we consider an $\ell_{0}$-norm penalized formulation of the generalized eigenvalue problem (GEP), aimed at extracting the leading sparse generalized eigenvector of a matrix pair. The formulation involves maximization of a discontinuous nonconcave objective function over a nonconvex constraint set, and is therefore computationally intractable. To tackle the problem, we first approximate the $\ell_{0}$-norm by a continuous surrogate function. Then an algorithm is developed via iteratively majorizing the surrogate function by a quadratic separable function, which at each iteration reduces to a regular generalized eigenvalue problem. A preconditioned steepest ascent algorithm for finding the leading generalized eigenvector is provided. A systematic way based on smoothing is proposed to deal with the "singularity issue" that arises when a quadratic function is used to majorize the nondifferentiable surrogate function. For sparse GEPs with special structure, algorithms that admit a closed-form solution at every iteration are derived. Numerical experiments show that the proposed algorithms match or outperform existing algorithms in terms of computational complexity and support recovery.