Conditional Memory via Scalable Lookup: A New Axis of Sparsity for Large Language Models

While Mixture-of-Experts (MoE) scales capacity via conditional computation, Transformers lack a native primitive for knowledge lookup, forcing them to inefficiently simulate retrieval through computation. To address this, we introduce conditional memory as a complementary sparsity axis, instantiated via Engram, a module that modernizes classic $N$-gram embedding for O(1) lookup. By formulating the Sparsity Allocation problem, we uncover a U-shaped scaling law that optimizes the trade-off between neural computation (MoE) and static memory (Engram). Guided by this law, we scale Engram to 27B parameters, achieving superior performance over a strictly iso-parameter and iso-FLOPs MoE baseline. Most notably, while the memory module is expected to aid knowledge retrieval (e.g., MMLU +3.4; CMMLU +4.0), we observe even larger gains in general reasoning (e.g., BBH +5.0; ARC-Challenge +3.7) and code/math domains~(HumanEval +3.0; MATH +2.4). Mechanistic analyses reveal that Engram relieves the backbone's early layers from static reconstruction, effectively deepening the network for complex reasoning. Furthermore, by delegating local dependencies to lookups, it frees up attention capacity for global context, substantially boosting long-context retrieval (e.g., Multi-Query NIAH: 84.2 to 97.0). Finally, Engram establishes infrastructure-aware efficiency: its deterministic addressing enables runtime prefetching from host memory, incurring negligible overhead. We envision conditional memory as an indispensable modeling primitive for next-generation sparse models.

mHC: Manifold-Constrained Hyper-Connections

Recently, studies exemplified by Hyper-Connections (HC) have extended the ubiquitous residual connection paradigm established over the past decade by expanding the residual stream width and diversifying connectivity patterns. While yielding substantial performance gains, this diversification fundamentally compromises the identity mapping property intrinsic to the residual connection, which causes severe training instability and restricted scalability, and additionally incurs notable memory access overhead. To address these challenges, we propose Manifold-Constrained Hyper-Connections (mHC), a general framework that projects the residual connection space of HC onto a specific manifold to restore the identity mapping property, while incorporating rigorous infrastructure optimization to ensure efficiency. Empirical experiments demonstrate that mHC is effective for training at scale, offering tangible performance improvements and superior scalability. We anticipate that mHC, as a flexible and practical extension of HC, will contribute to a deeper understanding of topological architecture design and suggest promising directions for the evolution of foundational models.

Insights into DeepSeek-V3: Scaling Challenges and Reflections on Hardware for AI Architectures

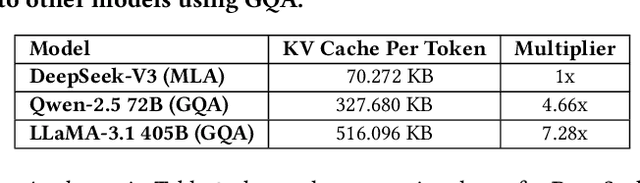
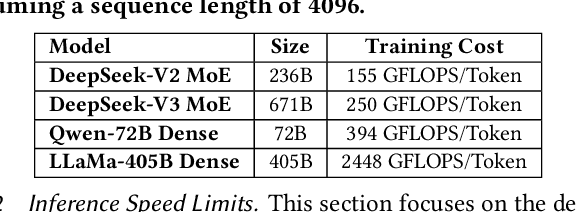
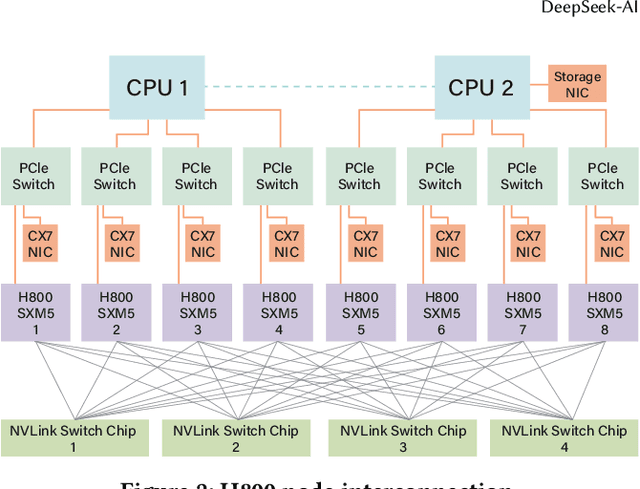
The rapid scaling of large language models (LLMs) has unveiled critical limitations in current hardware architectures, including constraints in memory capacity, computational efficiency, and interconnection bandwidth. DeepSeek-V3, trained on 2,048 NVIDIA H800 GPUs, demonstrates how hardware-aware model co-design can effectively address these challenges, enabling cost-efficient training and inference at scale. This paper presents an in-depth analysis of the DeepSeek-V3/R1 model architecture and its AI infrastructure, highlighting key innovations such as Multi-head Latent Attention (MLA) for enhanced memory efficiency, Mixture of Experts (MoE) architectures for optimized computation-communication trade-offs, FP8 mixed-precision training to unlock the full potential of hardware capabilities, and a Multi-Plane Network Topology to minimize cluster-level network overhead. Building on the hardware bottlenecks encountered during DeepSeek-V3's development, we engage in a broader discussion with academic and industry peers on potential future hardware directions, including precise low-precision computation units, scale-up and scale-out convergence, and innovations in low-latency communication fabrics. These insights underscore the critical role of hardware and model co-design in meeting the escalating demands of AI workloads, offering a practical blueprint for innovation in next-generation AI systems.

DeepSeek-V3 Technical Report

We present DeepSeek-V3, a strong Mixture-of-Experts (MoE) language model with 671B total parameters with 37B activated for each token. To achieve efficient inference and cost-effective training, DeepSeek-V3 adopts Multi-head Latent Attention (MLA) and DeepSeekMoE architectures, which were thoroughly validated in DeepSeek-V2. Furthermore, DeepSeek-V3 pioneers an auxiliary-loss-free strategy for load balancing and sets a multi-token prediction training objective for stronger performance. We pre-train DeepSeek-V3 on 14.8 trillion diverse and high-quality tokens, followed by Supervised Fine-Tuning and Reinforcement Learning stages to fully harness its capabilities. Comprehensive evaluations reveal that DeepSeek-V3 outperforms other open-source models and achieves performance comparable to leading closed-source models. Despite its excellent performance, DeepSeek-V3 requires only 2.788M H800 GPU hours for its full training. In addition, its training process is remarkably stable. Throughout the entire training process, we did not experience any irrecoverable loss spikes or perform any rollbacks. The model checkpoints are available at https://github.com/deepseek-ai/DeepSeek-V3.

DeepSeek-VL2: Mixture-of-Experts Vision-Language Models for Advanced Multimodal Understanding

We present DeepSeek-VL2, an advanced series of large Mixture-of-Experts (MoE) Vision-Language Models that significantly improves upon its predecessor, DeepSeek-VL, through two key major upgrades. For the vision component, we incorporate a dynamic tiling vision encoding strategy designed for processing high-resolution images with different aspect ratios. For the language component, we leverage DeepSeekMoE models with the Multi-head Latent Attention mechanism, which compresses Key-Value cache into latent vectors, to enable efficient inference and high throughput. Trained on an improved vision-language dataset, DeepSeek-VL2 demonstrates superior capabilities across various tasks, including but not limited to visual question answering, optical character recognition, document/table/chart understanding, and visual grounding. Our model series is composed of three variants: DeepSeek-VL2-Tiny, DeepSeek-VL2-Small and DeepSeek-VL2, with 1.0B, 2.8B and 4.5B activated parameters respectively. DeepSeek-VL2 achieves competitive or state-of-the-art performance with similar or fewer activated parameters compared to existing open-source dense and MoE-based models. Codes and pre-trained models are publicly accessible at https://github.com/deepseek-ai/DeepSeek-VL2.

Auxiliary-Loss-Free Load Balancing Strategy for Mixture-of-Experts

For Mixture-of-Experts (MoE) models, an unbalanced expert load will lead to routing collapse or increased computational overhead. Existing methods commonly employ an auxiliary loss to encourage load balance, but a large auxiliary loss will introduce non-negligible interference gradients into training and thus impair the model performance. In order to control load balance while not producing undesired gradients during training, we propose Loss-Free Balancing, featured by an auxiliary-loss-free load balancing strategy. To be specific, before the top-K routing decision, Loss-Free Balancing will first apply an expert-wise bias to the routing scores of each expert. By dynamically updating the bias of each expert according to its recent load, Loss-Free Balancing can consistently maintain a balanced distribution of expert load. In addition, since Loss-Free Balancing does not produce any interference gradients, it also elevates the upper bound of model performance gained from MoE training. We validate the performance of Loss-Free Balancing on MoE models with up to 3B parameters trained on up to 200B tokens. Experimental results show that Loss-Free Balancing achieves both better performance and better load balance compared with traditional auxiliary-loss-controlled load balancing strategies.

Let the Expert Stick to His Last: Expert-Specialized Fine-Tuning for Sparse Architectural Large Language Models

Parameter-efficient fine-tuning (PEFT) is crucial for customizing Large Language Models (LLMs) with constrained resources. Although there have been various PEFT methods for dense-architecture LLMs, PEFT for sparse-architecture LLMs is still underexplored. In this work, we study the PEFT method for LLMs with the Mixture-of-Experts (MoE) architecture and the contents of this work are mainly threefold: (1) We investigate the dispersion degree of the activated experts in customized tasks, and found that the routing distribution for a specific task tends to be highly concentrated, while the distribution of activated experts varies significantly across different tasks. (2) We propose Expert-Specialized Fine-Tuning, or ESFT, which tunes the experts most relevant to downstream tasks while freezing the other experts and modules; experimental results demonstrate that our method not only improves the tuning efficiency, but also matches or even surpasses the performance of full-parameter fine-tuning. (3) We further analyze the impact of the MoE architecture on expert-specialized fine-tuning. We find that MoE models with finer-grained experts are more advantageous in selecting the combination of experts that are most relevant to downstream tasks, thereby enhancing both the training efficiency and effectiveness.

DeepSeek-Coder-V2: Breaking the Barrier of Closed-Source Models in Code Intelligence

We present DeepSeek-Coder-V2, an open-source Mixture-of-Experts (MoE) code language model that achieves performance comparable to GPT4-Turbo in code-specific tasks. Specifically, DeepSeek-Coder-V2 is further pre-trained from an intermediate checkpoint of DeepSeek-V2 with additional 6 trillion tokens. Through this continued pre-training, DeepSeek-Coder-V2 substantially enhances the coding and mathematical reasoning capabilities of DeepSeek-V2, while maintaining comparable performance in general language tasks. Compared to DeepSeek-Coder-33B, DeepSeek-Coder-V2 demonstrates significant advancements in various aspects of code-related tasks, as well as reasoning and general capabilities. Additionally, DeepSeek-Coder-V2 expands its support for programming languages from 86 to 338, while extending the context length from 16K to 128K. In standard benchmark evaluations, DeepSeek-Coder-V2 achieves superior performance compared to closed-source models such as GPT4-Turbo, Claude 3 Opus, and Gemini 1.5 Pro in coding and math benchmarks.

Exploring Activation Patterns of Parameters in Language Models

Most work treats large language models as black boxes without in-depth understanding of their internal working mechanism. In order to explain the internal representations of LLMs, we propose a gradient-based metric to assess the activation level of model parameters. Based on this metric, we obtain three preliminary findings. (1) When the inputs are in the same domain, parameters in the shallow layers will be activated densely, which means a larger portion of parameters will have great impacts on the outputs. In contrast, parameters in the deep layers are activated sparsely. (2) When the inputs are across different domains, parameters in shallow layers exhibit higher similarity in the activation behavior than deep layers. (3) In deep layers, the similarity of the distributions of activated parameters is positively correlated to the empirical data relevance. Further, we develop three validation experiments to solidify these findings. (1) Firstly, starting from the first finding, we attempt to configure different prune ratios for different layers, and find this method can benefit model pruning. (2) Secondly, we find that a pruned model based on one calibration set can better handle tasks related to the calibration task than those not related, which validate the second finding. (3) Thirdly, Based on the STS-B and SICK benchmark, we find that two sentences with consistent semantics tend to share similar parameter activation patterns in deep layers, which aligns with our third finding. Our work sheds light on the behavior of parameter activation in LLMs, and we hope these findings will have the potential to inspire more practical applications.

Large Language Models Are Unconscious of Unreasonability in Math Problems

Large language models (LLMs) demonstrate substantial capabilities in solving math problems. However, they tend to produce hallucinations when given questions containing unreasonable errors. In this paper, we study the behavior of LLMs when faced with unreasonable math problems and further explore their potential to address these problems. First, we construct the Unreasonable Math Problem (UMP) benchmark to examine the error detection ability of LLMs. Experiments show that LLMs are able to detect unreasonable errors, but still fail in generating non-hallucinatory content. In order to improve their ability of error detection and correction, we further design a strategic prompt template called Critical Calculation and Conclusion(CCC). With CCC, LLMs can better self-evaluate and detect unreasonable errors in math questions, making them more reliable and safe in practical application scenarios.