Xun Zheng
Learning Sparse Nonparametric DAGs
Sep 29, 2019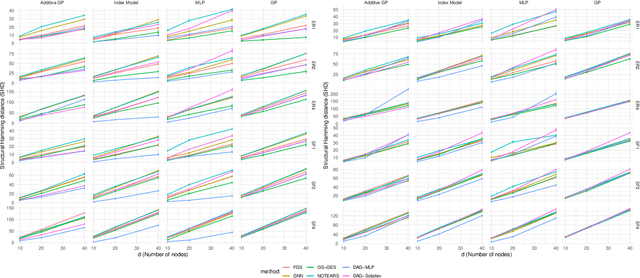


Abstract:We develop a framework for learning sparse nonparametric directed acyclic graphs (DAGs) from data. Our approach is based on a recent algebraic characterization of DAGs that led to the first fully continuous optimization for score-based learning of DAG models parametrized by a linear structural equation model (SEM). We extend this algebraic characterization to nonparametric SEM by leveraging nonparametric sparsity based on partial derivatives, resulting in a continuous optimization problem that can be applied to a variety of nonparametric and semiparametric models including GLMs, additive noise models, and index models as special cases. We also explore the use of neural networks and orthogonal basis expansions to model nonlinearities for general nonparametric models. Extensive empirical study confirms the necessity of nonlinear dependency and the advantage of continuous optimization for score-based learning.
DAGs with NO TEARS: Continuous Optimization for Structure Learning
Nov 03, 2018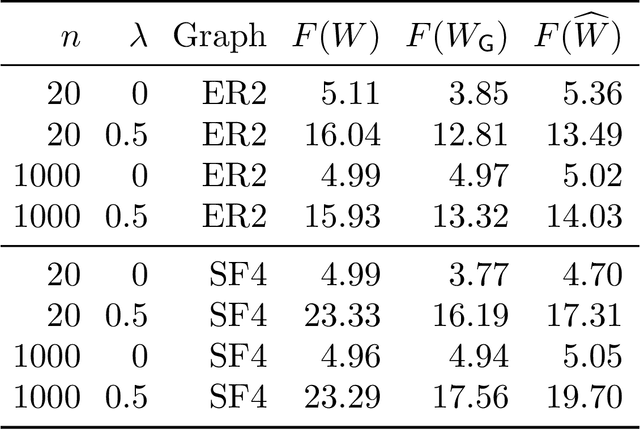
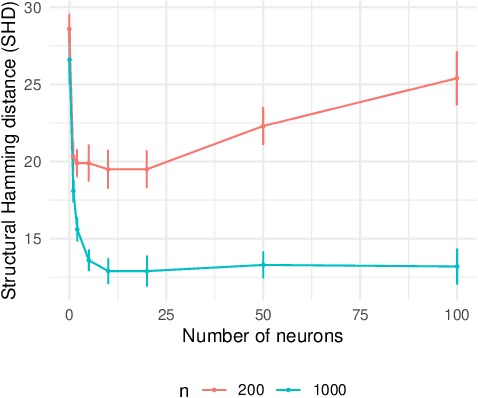
Abstract:Estimating the structure of directed acyclic graphs (DAGs, also known as Bayesian networks) is a challenging problem since the search space of DAGs is combinatorial and scales superexponentially with the number of nodes. Existing approaches rely on various local heuristics for enforcing the acyclicity constraint. In this paper, we introduce a fundamentally different strategy: We formulate the structure learning problem as a purely \emph{continuous} optimization problem over real matrices that avoids this combinatorial constraint entirely. This is achieved by a novel characterization of acyclicity that is not only smooth but also exact. The resulting problem can be efficiently solved by standard numerical algorithms, which also makes implementation effortless. The proposed method outperforms existing ones, without imposing any structural assumptions on the graph such as bounded treewidth or in-degree. Code implementing the proposed algorithm is open-source and publicly available at https://github.com/xunzheng/notears.
Learning Tensor Latent Features
Oct 10, 2018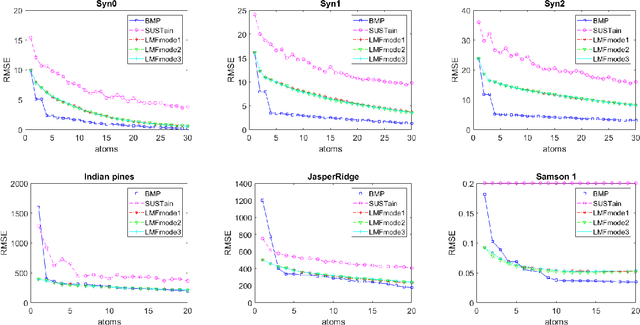
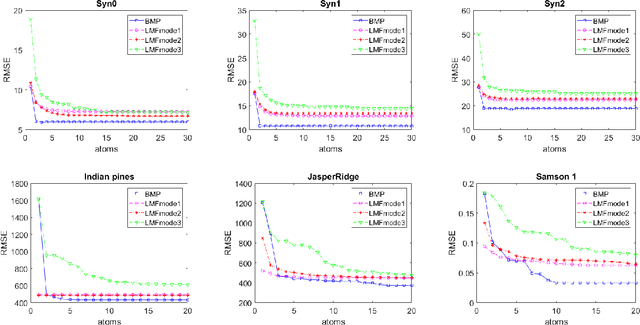
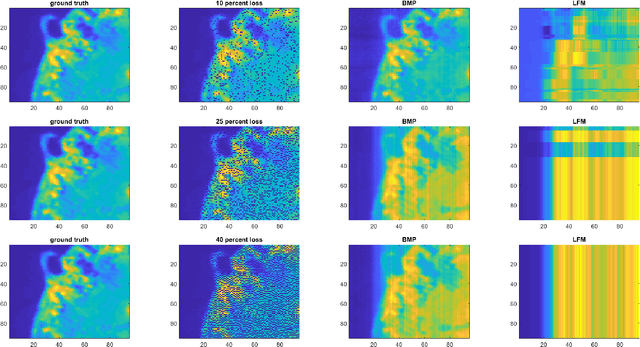
Abstract:We study the problem of learning latent feature models (LFMs) for tensor data commonly observed in science and engineering such as hyperspectral imagery. However, the problem is challenging not only due to the non-convex formulation, the combinatorial nature of the constraints in LFMs, but also the high-order correlations in the data. In this work, we formulate a tensor latent feature learning problem by representing the data as a mixture of high-order latent features and binary codes, which are memory efficient and easy to interpret. To make the learning tractable, we propose a novel optimization procedure, Binary matching pursuit (BMP), that iteratively searches for binary bases via a MAXCUT-like boolean quadratic solver. Such a procedure is guaranteed to achieve an? suboptimal solution in O($1/\epsilon$) greedy steps, resulting in a trade-off between accuracy and sparsity. When evaluated on both synthetic and real datasets, our experiments show superior performance over baseline methods.
State Space LSTM Models with Particle MCMC Inference
Nov 30, 2017



Abstract:Long Short-Term Memory (LSTM) is one of the most powerful sequence models. Despite the strong performance, however, it lacks the nice interpretability as in state space models. In this paper, we present a way to combine the best of both worlds by introducing State Space LSTM (SSL) models that generalizes the earlier work \cite{zaheer2017latent} of combining topic models with LSTM. However, unlike \cite{zaheer2017latent}, we do not make any factorization assumptions in our inference algorithm. We present an efficient sampler based on sequential Monte Carlo (SMC) method that draws from the joint posterior directly. Experimental results confirms the superiority and stability of this SMC inference algorithm on a variety of domains.
Petuum: A New Platform for Distributed Machine Learning on Big Data
May 14, 2015

Abstract:What is a systematic way to efficiently apply a wide spectrum of advanced ML programs to industrial scale problems, using Big Models (up to 100s of billions of parameters) on Big Data (up to terabytes or petabytes)? Modern parallelization strategies employ fine-grained operations and scheduling beyond the classic bulk-synchronous processing paradigm popularized by MapReduce, or even specialized graph-based execution that relies on graph representations of ML programs. The variety of approaches tends to pull systems and algorithms design in different directions, and it remains difficult to find a universal platform applicable to a wide range of ML programs at scale. We propose a general-purpose framework that systematically addresses data- and model-parallel challenges in large-scale ML, by observing that many ML programs are fundamentally optimization-centric and admit error-tolerant, iterative-convergent algorithmic solutions. This presents unique opportunities for an integrative system design, such as bounded-error network synchronization and dynamic scheduling based on ML program structure. We demonstrate the efficacy of these system designs versus well-known implementations of modern ML algorithms, allowing ML programs to run in much less time and at considerably larger model sizes, even on modestly-sized compute clusters.
LightLDA: Big Topic Models on Modest Compute Clusters
Dec 04, 2014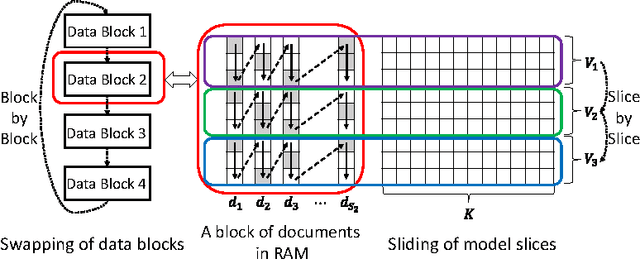

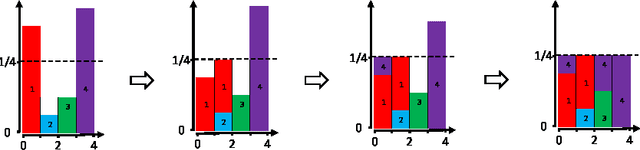
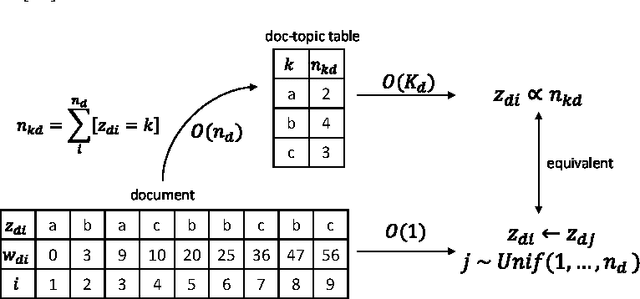
Abstract:When building large-scale machine learning (ML) programs, such as big topic models or deep neural nets, one usually assumes such tasks can only be attempted with industrial-sized clusters with thousands of nodes, which are out of reach for most practitioners or academic researchers. We consider this challenge in the context of topic modeling on web-scale corpora, and show that with a modest cluster of as few as 8 machines, we can train a topic model with 1 million topics and a 1-million-word vocabulary (for a total of 1 trillion parameters), on a document collection with 200 billion tokens -- a scale not yet reported even with thousands of machines. Our major contributions include: 1) a new, highly efficient O(1) Metropolis-Hastings sampling algorithm, whose running cost is (surprisingly) agnostic of model size, and empirically converges nearly an order of magnitude faster than current state-of-the-art Gibbs samplers; 2) a structure-aware model-parallel scheme, which leverages dependencies within the topic model, yielding a sampling strategy that is frugal on machine memory and network communication; 3) a differential data-structure for model storage, which uses separate data structures for high- and low-frequency words to allow extremely large models to fit in memory, while maintaining high inference speed; and 4) a bounded asynchronous data-parallel scheme, which allows efficient distributed processing of massive data via a parameter server. Our distribution strategy is an instance of the model-and-data-parallel programming model underlying the Petuum framework for general distributed ML, and was implemented on top of the Petuum open-source system. We provide experimental evidence showing how this development puts massive models within reach on a small cluster while still enjoying proportional time cost reductions with increasing cluster size, in comparison with alternative options.
Model-Parallel Inference for Big Topic Models
Nov 10, 2014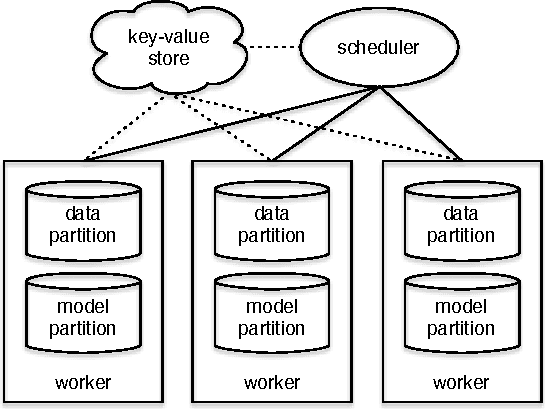

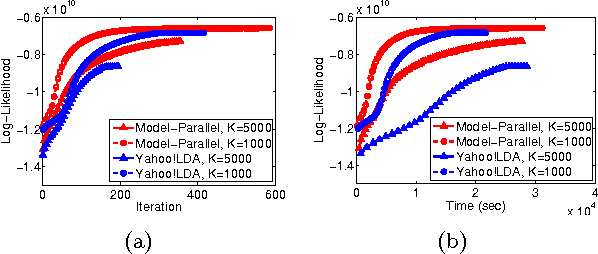
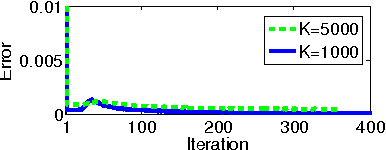
Abstract:In real world industrial applications of topic modeling, the ability to capture gigantic conceptual space by learning an ultra-high dimensional topical representation, i.e., the so-called "big model", is becoming the next desideratum after enthusiasms on "big data", especially for fine-grained downstream tasks such as online advertising, where good performances are usually achieved by regression-based predictors built on millions if not billions of input features. The conventional data-parallel approach for training gigantic topic models turns out to be rather inefficient in utilizing the power of parallelism, due to the heavy dependency on a centralized image of "model". Big model size also poses another challenge on the storage, where available model size is bounded by the smallest RAM of nodes. To address these issues, we explore another type of parallelism, namely model-parallelism, which enables training of disjoint blocks of a big topic model in parallel. By integrating data-parallelism with model-parallelism, we show that dependencies between distributed elements can be handled seamlessly, achieving not only faster convergence but also an ability to tackle significantly bigger model size. We describe an architecture for model-parallel inference of LDA, and present a variant of collapsed Gibbs sampling algorithm tailored for it. Experimental results demonstrate the ability of this system to handle topic modeling with unprecedented amount of 200 billion model variables only on a low-end cluster with very limited computational resources and bandwidth.
Primitives for Dynamic Big Model Parallelism
Jun 18, 2014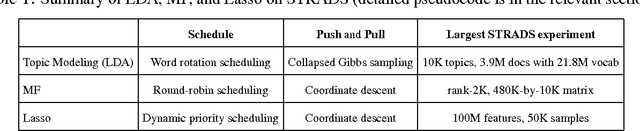
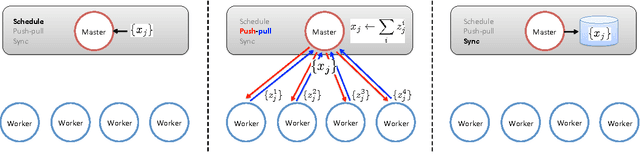

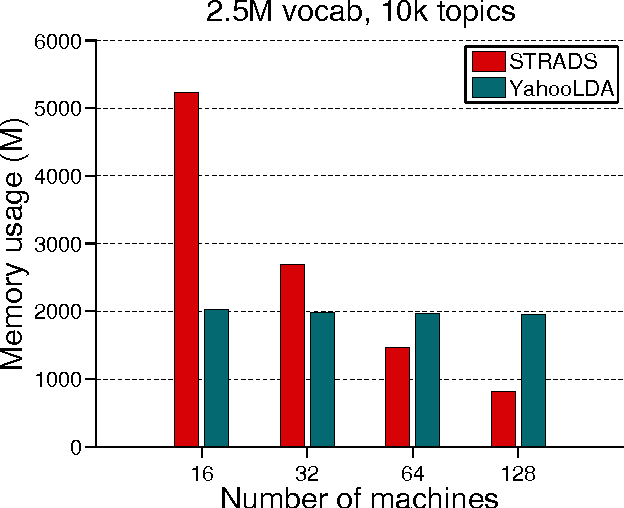
Abstract:When training large machine learning models with many variables or parameters, a single machine is often inadequate since the model may be too large to fit in memory, while training can take a long time even with stochastic updates. A natural recourse is to turn to distributed cluster computing, in order to harness additional memory and processors. However, naive, unstructured parallelization of ML algorithms can make inefficient use of distributed memory, while failing to obtain proportional convergence speedups - or can even result in divergence. We develop a framework of primitives for dynamic model-parallelism, STRADS, in order to explore partitioning and update scheduling of model variables in distributed ML algorithms - thus improving their memory efficiency while presenting new opportunities to speed up convergence without compromising inference correctness. We demonstrate the efficacy of model-parallel algorithms implemented in STRADS versus popular implementations for Topic Modeling, Matrix Factorization and Lasso.
Consistent Bounded-Asynchronous Parameter Servers for Distributed ML
Dec 31, 2013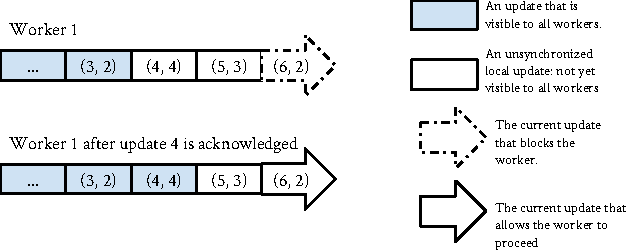

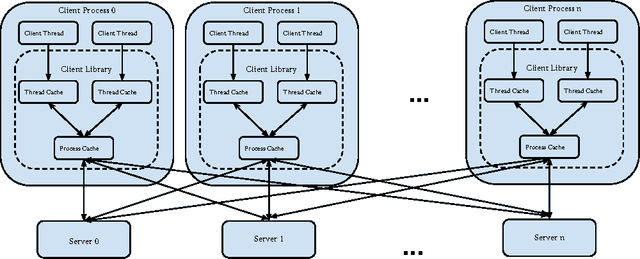
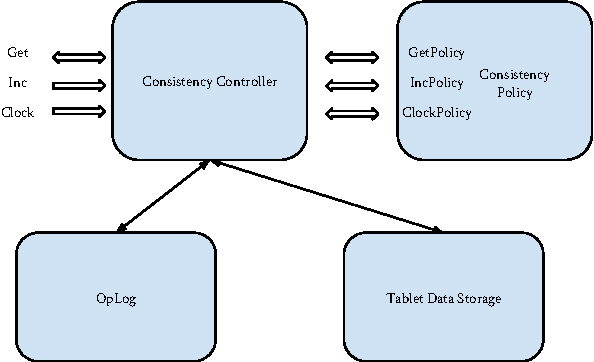
Abstract:In distributed ML applications, shared parameters are usually replicated among computing nodes to minimize network overhead. Therefore, proper consistency model must be carefully chosen to ensure algorithm's correctness and provide high throughput. Existing consistency models used in general-purpose databases and modern distributed ML systems are either too loose to guarantee correctness of the ML algorithms or too strict and thus fail to fully exploit the computing power of the underlying distributed system. Many ML algorithms fall into the category of \emph{iterative convergent algorithms} which start from a randomly chosen initial point and converge to optima by repeating iteratively a set of procedures. We've found that many such algorithms are to a bounded amount of inconsistency and still converge correctly. This property allows distributed ML to relax strict consistency models to improve system performance while theoretically guarantees algorithmic correctness. In this paper, we present several relaxed consistency models for asynchronous parallel computation and theoretically prove their algorithmic correctness. The proposed consistency models are implemented in a distributed parameter server and evaluated in the context of a popular ML application: topic modeling.
Improved Bayesian Logistic Supervised Topic Models with Data Augmentation
Oct 09, 2013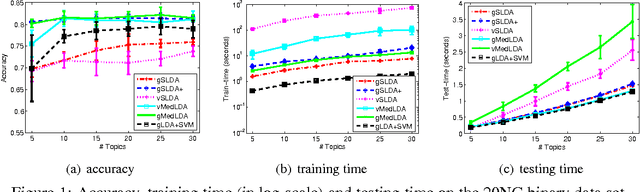

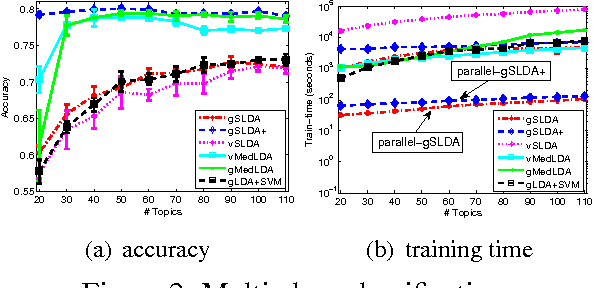
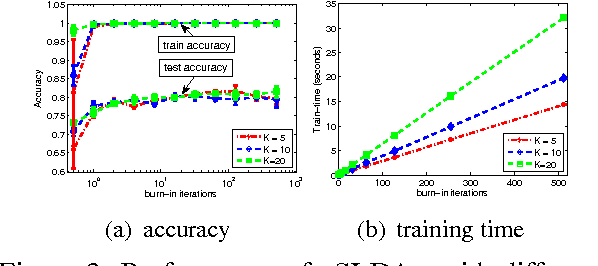
Abstract:Supervised topic models with a logistic likelihood have two issues that potentially limit their practical use: 1) response variables are usually over-weighted by document word counts; and 2) existing variational inference methods make strict mean-field assumptions. We address these issues by: 1) introducing a regularization constant to better balance the two parts based on an optimization formulation of Bayesian inference; and 2) developing a simple Gibbs sampling algorithm by introducing auxiliary Polya-Gamma variables and collapsing out Dirichlet variables. Our augment-and-collapse sampling algorithm has analytical forms of each conditional distribution without making any restricting assumptions and can be easily parallelized. Empirical results demonstrate significant improvements on prediction performance and time efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge