Jin Kyu Kim
Pippo: High-Resolution Multi-View Humans from a Single Image
Feb 11, 2025
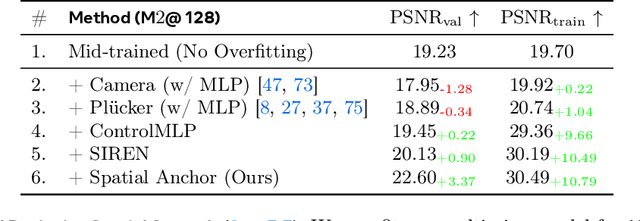
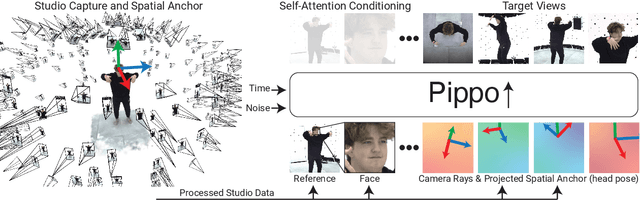

Abstract:We present Pippo, a generative model capable of producing 1K resolution dense turnaround videos of a person from a single casually clicked photo. Pippo is a multi-view diffusion transformer and does not require any additional inputs - e.g., a fitted parametric model or camera parameters of the input image. We pre-train Pippo on 3B human images without captions, and conduct multi-view mid-training and post-training on studio captured humans. During mid-training, to quickly absorb the studio dataset, we denoise several (up to 48) views at low-resolution, and encode target cameras coarsely using a shallow MLP. During post-training, we denoise fewer views at high-resolution and use pixel-aligned controls (e.g., Spatial anchor and Plucker rays) to enable 3D consistent generations. At inference, we propose an attention biasing technique that allows Pippo to simultaneously generate greater than 5 times as many views as seen during training. Finally, we also introduce an improved metric to evaluate 3D consistency of multi-view generations, and show that Pippo outperforms existing works on multi-view human generation from a single image.
Distributed Machine Learning via Sufficient Factor Broadcasting
Nov 26, 2015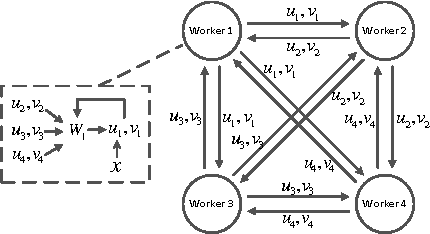
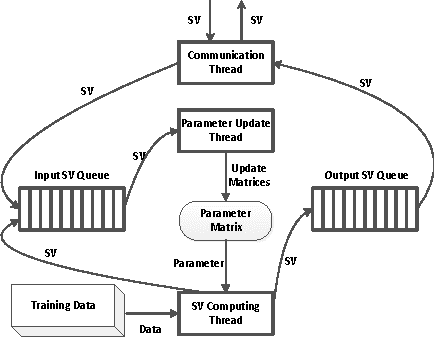


Abstract:Matrix-parametrized models, including multiclass logistic regression and sparse coding, are used in machine learning (ML) applications ranging from computer vision to computational biology. When these models are applied to large-scale ML problems starting at millions of samples and tens of thousands of classes, their parameter matrix can grow at an unexpected rate, resulting in high parameter synchronization costs that greatly slow down distributed learning. To address this issue, we propose a Sufficient Factor Broadcasting (SFB) computation model for efficient distributed learning of a large family of matrix-parameterized models, which share the following property: the parameter update computed on each data sample is a rank-1 matrix, i.e., the outer product of two "sufficient factors" (SFs). By broadcasting the SFs among worker machines and reconstructing the update matrices locally at each worker, SFB improves communication efficiency --- communication costs are linear in the parameter matrix's dimensions, rather than quadratic --- without affecting computational correctness. We present a theoretical convergence analysis of SFB, and empirically corroborate its efficiency on four different matrix-parametrized ML models.
Petuum: A New Platform for Distributed Machine Learning on Big Data
May 14, 2015

Abstract:What is a systematic way to efficiently apply a wide spectrum of advanced ML programs to industrial scale problems, using Big Models (up to 100s of billions of parameters) on Big Data (up to terabytes or petabytes)? Modern parallelization strategies employ fine-grained operations and scheduling beyond the classic bulk-synchronous processing paradigm popularized by MapReduce, or even specialized graph-based execution that relies on graph representations of ML programs. The variety of approaches tends to pull systems and algorithms design in different directions, and it remains difficult to find a universal platform applicable to a wide range of ML programs at scale. We propose a general-purpose framework that systematically addresses data- and model-parallel challenges in large-scale ML, by observing that many ML programs are fundamentally optimization-centric and admit error-tolerant, iterative-convergent algorithmic solutions. This presents unique opportunities for an integrative system design, such as bounded-error network synchronization and dynamic scheduling based on ML program structure. We demonstrate the efficacy of these system designs versus well-known implementations of modern ML algorithms, allowing ML programs to run in much less time and at considerably larger model sizes, even on modestly-sized compute clusters.
Model-Parallel Inference for Big Topic Models
Nov 10, 2014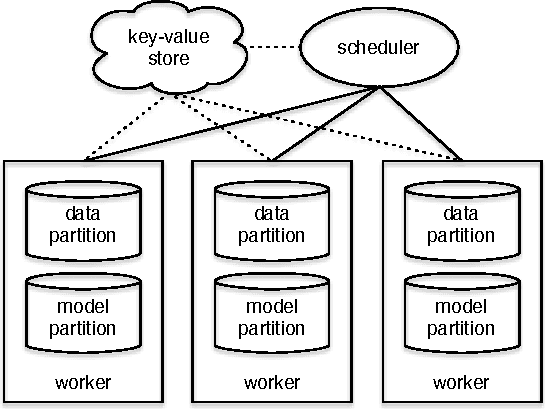

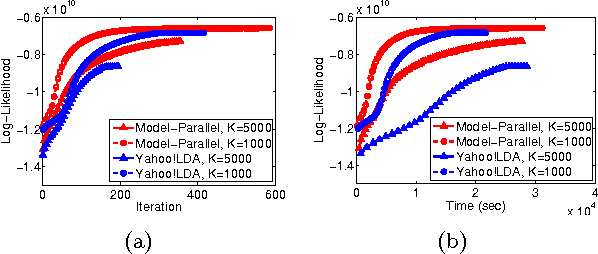
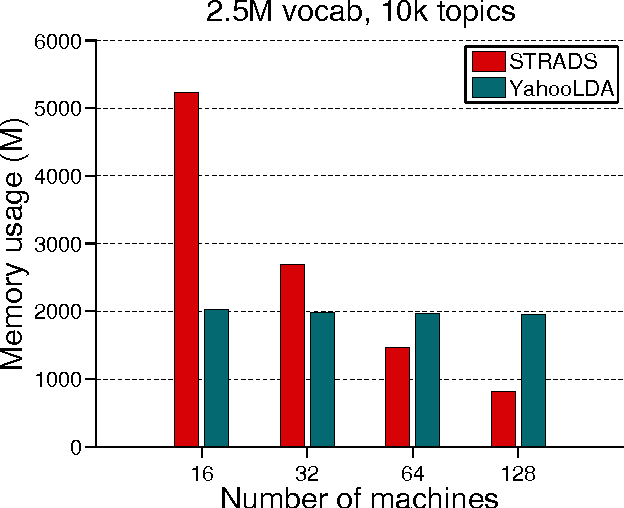
Abstract:In real world industrial applications of topic modeling, the ability to capture gigantic conceptual space by learning an ultra-high dimensional topical representation, i.e., the so-called "big model", is becoming the next desideratum after enthusiasms on "big data", especially for fine-grained downstream tasks such as online advertising, where good performances are usually achieved by regression-based predictors built on millions if not billions of input features. The conventional data-parallel approach for training gigantic topic models turns out to be rather inefficient in utilizing the power of parallelism, due to the heavy dependency on a centralized image of "model". Big model size also poses another challenge on the storage, where available model size is bounded by the smallest RAM of nodes. To address these issues, we explore another type of parallelism, namely model-parallelism, which enables training of disjoint blocks of a big topic model in parallel. By integrating data-parallelism with model-parallelism, we show that dependencies between distributed elements can be handled seamlessly, achieving not only faster convergence but also an ability to tackle significantly bigger model size. We describe an architecture for model-parallel inference of LDA, and present a variant of collapsed Gibbs sampling algorithm tailored for it. Experimental results demonstrate the ability of this system to handle topic modeling with unprecedented amount of 200 billion model variables only on a low-end cluster with very limited computational resources and bandwidth.
Primitives for Dynamic Big Model Parallelism
Jun 18, 2014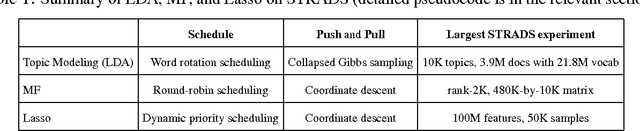
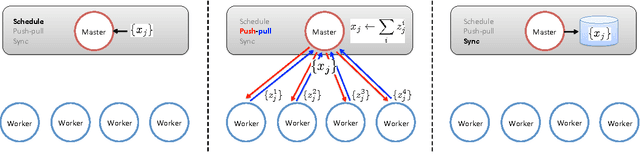

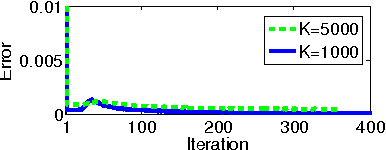
Abstract:When training large machine learning models with many variables or parameters, a single machine is often inadequate since the model may be too large to fit in memory, while training can take a long time even with stochastic updates. A natural recourse is to turn to distributed cluster computing, in order to harness additional memory and processors. However, naive, unstructured parallelization of ML algorithms can make inefficient use of distributed memory, while failing to obtain proportional convergence speedups - or can even result in divergence. We develop a framework of primitives for dynamic model-parallelism, STRADS, in order to explore partitioning and update scheduling of model variables in distributed ML algorithms - thus improving their memory efficiency while presenting new opportunities to speed up convergence without compromising inference correctness. We demonstrate the efficacy of model-parallel algorithms implemented in STRADS versus popular implementations for Topic Modeling, Matrix Factorization and Lasso.
Structure-Aware Dynamic Scheduler for Parallel Machine Learning
Dec 30, 2013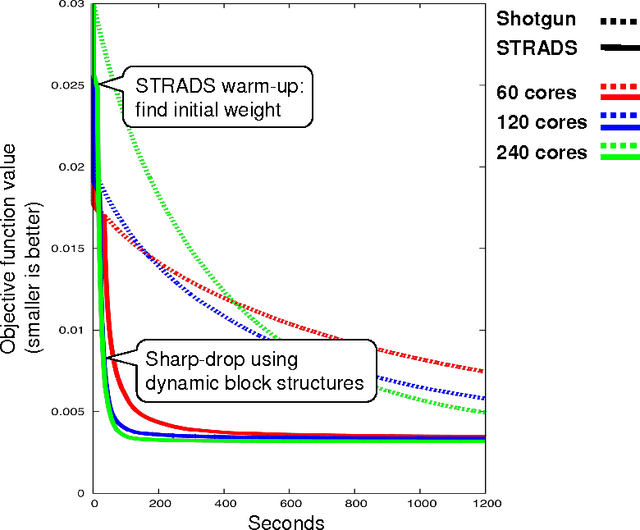
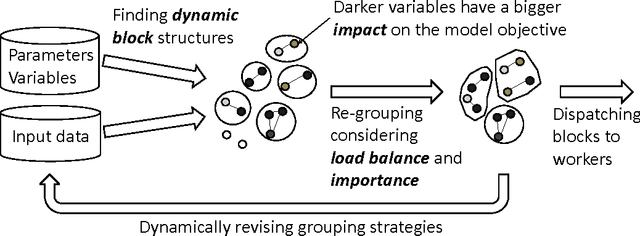
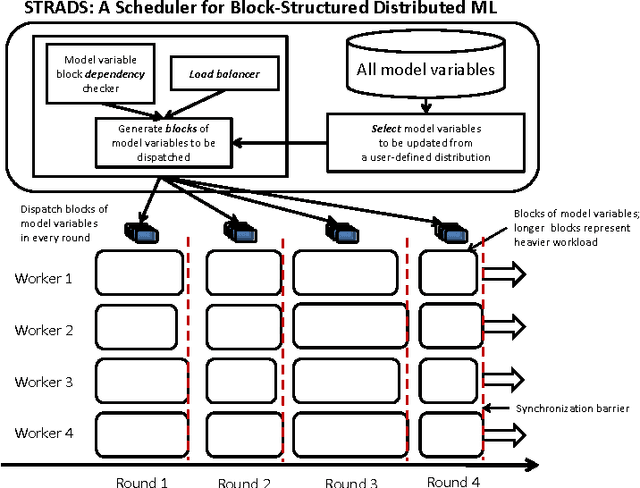
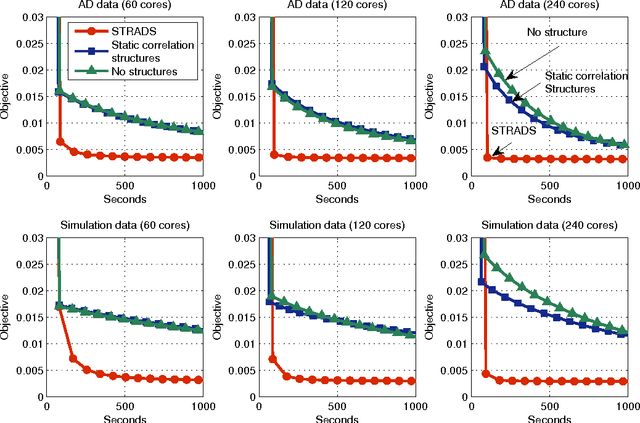
Abstract:Training large machine learning (ML) models with many variables or parameters can take a long time if one employs sequential procedures even with stochastic updates. A natural solution is to turn to distributed computing on a cluster; however, naive, unstructured parallelization of ML algorithms does not usually lead to a proportional speedup and can even result in divergence, because dependencies between model elements can attenuate the computational gains from parallelization and compromise correctness of inference. Recent efforts toward this issue have benefited from exploiting the static, a priori block structures residing in ML algorithms. In this paper, we take this path further by exploring the dynamic block structures and workloads therein present during ML program execution, which offers new opportunities for improving convergence, correctness, and load balancing in distributed ML. We propose and showcase a general-purpose scheduler, STRADS, for coordinating distributed updates in ML algorithms, which harnesses the aforementioned opportunities in a systematic way. We provide theoretical guarantees for our scheduler, and demonstrate its efficacy versus static block structures on Lasso and Matrix Factorization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge