Seunghak Lee
Fast Dimensional Analysis for Root Cause Investigation in Large-Scale Service Environment
Nov 01, 2019
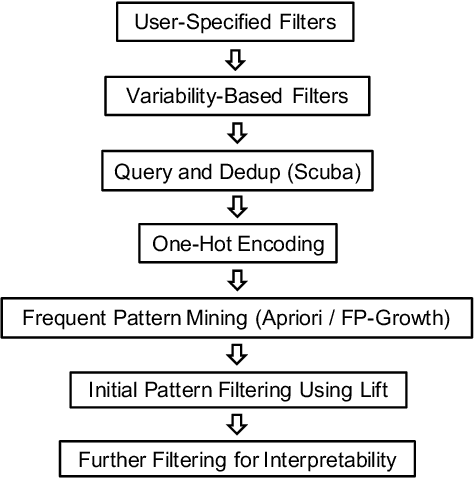
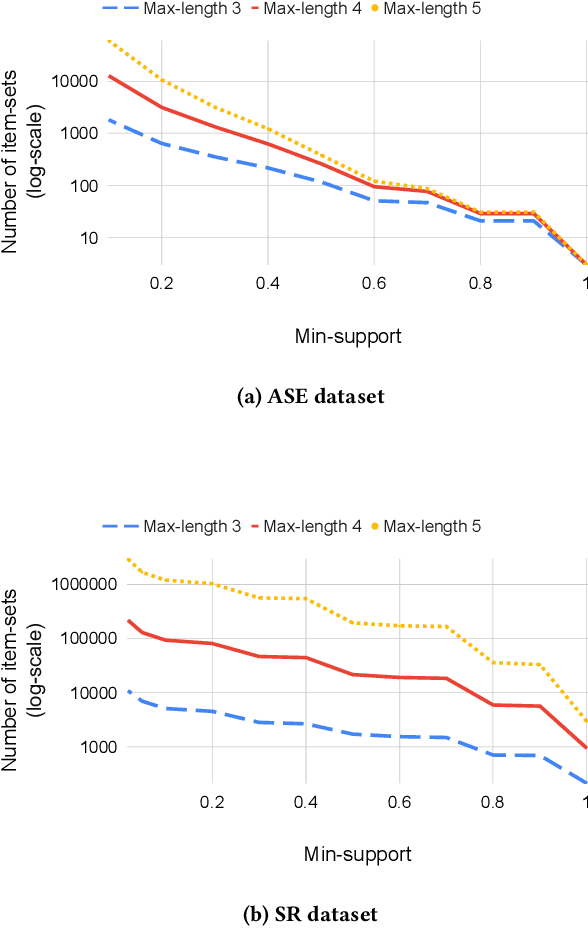
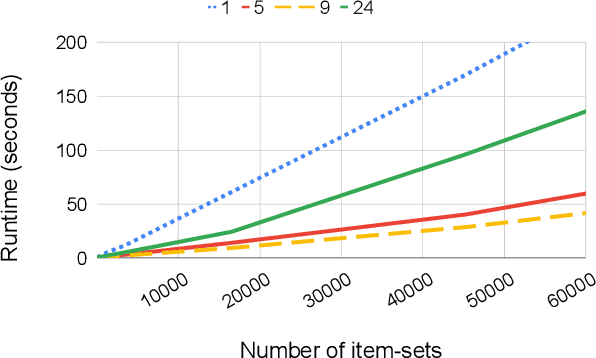
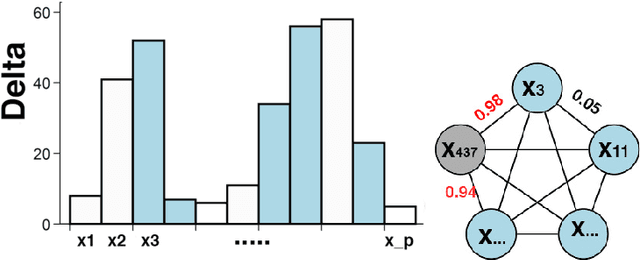
Abstract:Root cause analysis in a large-scale production environment is challenging due to the complexity of services running across global data centers. Due to the distributed nature of a large-scale system, the various hardware, software, and tooling logs are often maintained separately, making it difficult to review the logs jointly for detecting issues. Another challenge in reviewing the logs for identifying issues is the scale - there could easily be millions of entities, each with hundreds of features. In this paper we present a fast dimensional analysis framework that automates the root cause analysis on structured logs with improved scalability. We first explore item-sets, i.e. a group of feature values, that could identify groups of samples with sufficient support for the target failures using the Apriori algorithm and a subsequent improvement, FP-Growth. These algorithms were designed for frequent item-set mining and association rule learning over transactional databases. After applying them on structured logs, we select the item-sets that are most unique to the target failures based on lift. With the use of a large-scale real-time database, we propose pre- and post-processing techniques and parallelism to further speed up the analysis. We have successfully rolled out this approach for root cause investigation purposes in a large-scale infrastructure. We also present the setup and results from multiple production use-cases in this paper.
Stability Selection for Structured Variable Selection
Dec 13, 2017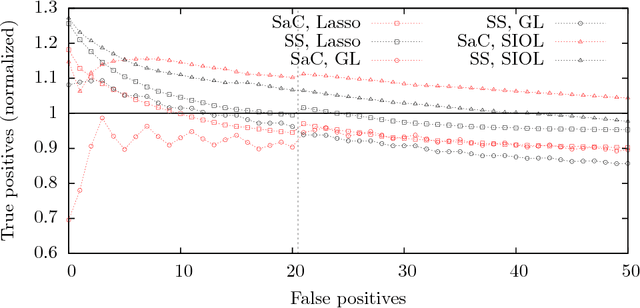
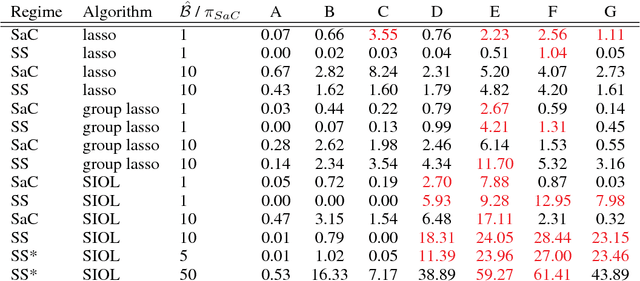
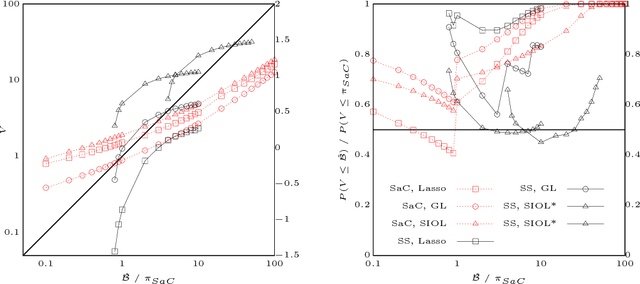
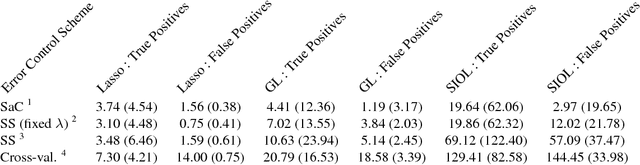
Abstract:In variable or graph selection problems, finding a right-sized model or controlling the number of false positives is notoriously difficult. Recently, a meta-algorithm called Stability Selection was proposed that can provide reliable finite-sample control of the number of false positives. Its benefits were demonstrated when used in conjunction with the lasso and orthogonal matching pursuit algorithms. In this paper, we investigate the applicability of stability selection to structured selection algorithms: the group lasso and the structured input-output lasso. We find that using stability selection often increases the power of both algorithms, but that the presence of complex structure reduces the reliability of error control under stability selection. We give strategies for setting tuning parameters to obtain a good model size under stability selection, and highlight its strengths and weaknesses compared to competing methods screen and clean and cross-validation. We give guidelines about when to use which error control method.
Petuum: A New Platform for Distributed Machine Learning on Big Data
May 14, 2015

Abstract:What is a systematic way to efficiently apply a wide spectrum of advanced ML programs to industrial scale problems, using Big Models (up to 100s of billions of parameters) on Big Data (up to terabytes or petabytes)? Modern parallelization strategies employ fine-grained operations and scheduling beyond the classic bulk-synchronous processing paradigm popularized by MapReduce, or even specialized graph-based execution that relies on graph representations of ML programs. The variety of approaches tends to pull systems and algorithms design in different directions, and it remains difficult to find a universal platform applicable to a wide range of ML programs at scale. We propose a general-purpose framework that systematically addresses data- and model-parallel challenges in large-scale ML, by observing that many ML programs are fundamentally optimization-centric and admit error-tolerant, iterative-convergent algorithmic solutions. This presents unique opportunities for an integrative system design, such as bounded-error network synchronization and dynamic scheduling based on ML program structure. We demonstrate the efficacy of these system designs versus well-known implementations of modern ML algorithms, allowing ML programs to run in much less time and at considerably larger model sizes, even on modestly-sized compute clusters.
Screening Rules for Overlapping Group Lasso
Oct 25, 2014



Abstract:Recently, to solve large-scale lasso and group lasso problems, screening rules have been developed, the goal of which is to reduce the problem size by efficiently discarding zero coefficients using simple rules independently of the others. However, screening for overlapping group lasso remains an open challenge because the overlaps between groups make it infeasible to test each group independently. In this paper, we develop screening rules for overlapping group lasso. To address the challenge arising from groups with overlaps, we take into account overlapping groups only if they are inclusive of the group being tested, and then we derive screening rules, adopting the dual polytope projection approach. This strategy allows us to screen each group independently of each other. In our experiments, we demonstrate the efficiency of our screening rules on various datasets.
Primitives for Dynamic Big Model Parallelism
Jun 18, 2014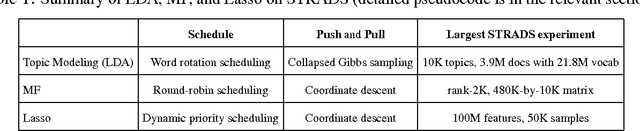
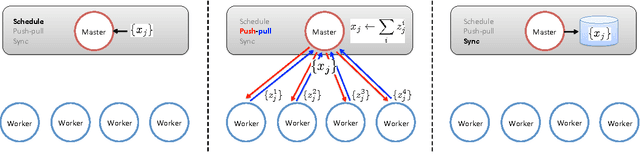

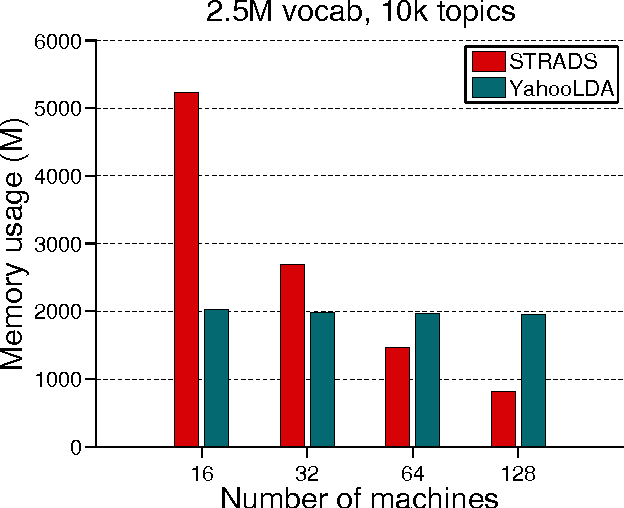
Abstract:When training large machine learning models with many variables or parameters, a single machine is often inadequate since the model may be too large to fit in memory, while training can take a long time even with stochastic updates. A natural recourse is to turn to distributed cluster computing, in order to harness additional memory and processors. However, naive, unstructured parallelization of ML algorithms can make inefficient use of distributed memory, while failing to obtain proportional convergence speedups - or can even result in divergence. We develop a framework of primitives for dynamic model-parallelism, STRADS, in order to explore partitioning and update scheduling of model variables in distributed ML algorithms - thus improving their memory efficiency while presenting new opportunities to speed up convergence without compromising inference correctness. We demonstrate the efficacy of model-parallel algorithms implemented in STRADS versus popular implementations for Topic Modeling, Matrix Factorization and Lasso.
Structure-Aware Dynamic Scheduler for Parallel Machine Learning
Dec 30, 2013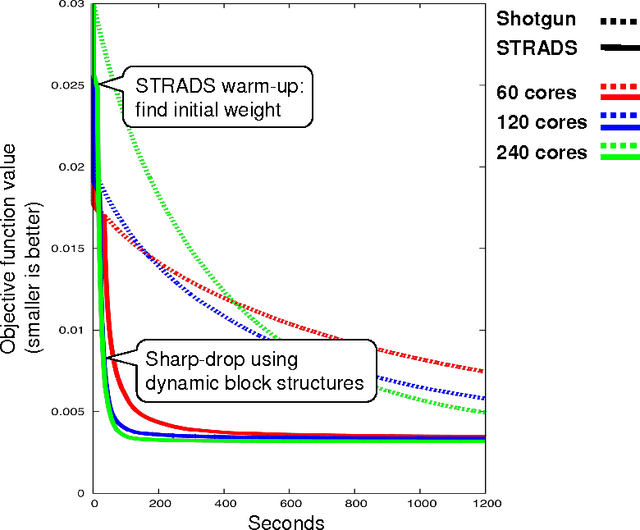
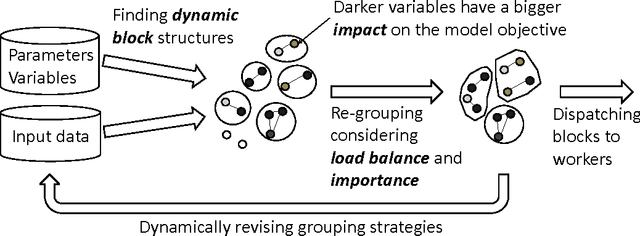
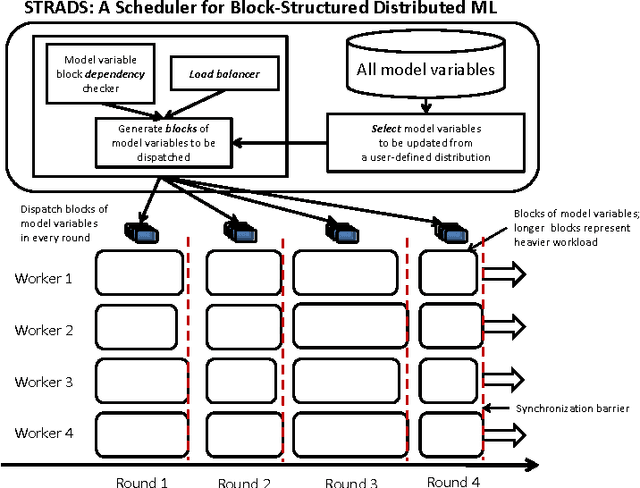
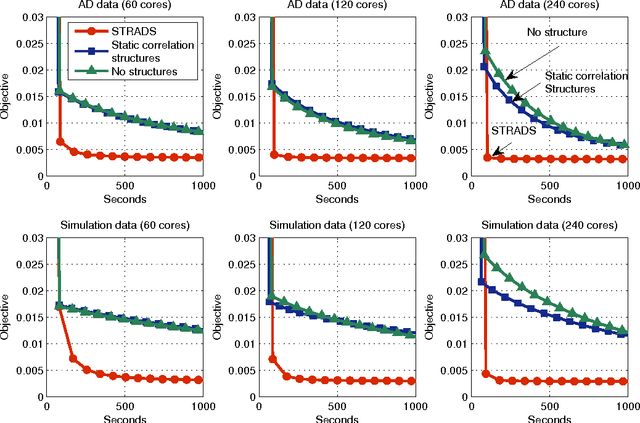
Abstract:Training large machine learning (ML) models with many variables or parameters can take a long time if one employs sequential procedures even with stochastic updates. A natural solution is to turn to distributed computing on a cluster; however, naive, unstructured parallelization of ML algorithms does not usually lead to a proportional speedup and can even result in divergence, because dependencies between model elements can attenuate the computational gains from parallelization and compromise correctness of inference. Recent efforts toward this issue have benefited from exploiting the static, a priori block structures residing in ML algorithms. In this paper, we take this path further by exploring the dynamic block structures and workloads therein present during ML program execution, which offers new opportunities for improving convergence, correctness, and load balancing in distributed ML. We propose and showcase a general-purpose scheduler, STRADS, for coordinating distributed updates in ML algorithms, which harnesses the aforementioned opportunities in a systematic way. We provide theoretical guarantees for our scheduler, and demonstrate its efficacy versus static block structures on Lasso and Matrix Factorization.
Efficient Algorithm for Extremely Large Multi-task Regression with Massive Structured Sparsity
Aug 15, 2012



Abstract:We develop a highly scalable optimization method called "hierarchical group-thresholding" for solving a multi-task regression model with complex structured sparsity constraints on both input and output spaces. Despite the recent emergence of several efficient optimization algorithms for tackling complex sparsity-inducing regularizers, true scalability in practical high-dimensional problems where a huge amount (e.g., millions) of sparsity patterns need to be enforced remains an open challenge, because all existing algorithms must deal with ALL such patterns exhaustively in every iteration, which is computationally prohibitive. Our proposed algorithm addresses the scalability problem by screening out multiple groups of coefficients simultaneously and systematically. We employ a hierarchical tree representation of group constraints to accelerate the process of removing irrelevant constraints by taking advantage of the inclusion relationships between group sparsities, thereby avoiding dealing with all constraints in every optimization step, and necessitating optimization operation only on a small number of outstanding coefficients. In our experiments, we demonstrate the efficiency of our method on simulation datasets, and in an application of detecting genetic variants associated with gene expression traits.
Structured Input-Output Lasso, with Application to eQTL Mapping, and a Thresholding Algorithm for Fast Estimation
May 09, 2012



Abstract:We consider the problem of learning a high-dimensional multi-task regression model, under sparsity constraints induced by presence of grouping structures on the input covariates and on the output predictors. This problem is primarily motivated by expression quantitative trait locus (eQTL) mapping, of which the goal is to discover genetic variations in the genome (inputs) that influence the expression levels of multiple co-expressed genes (outputs), either epistatically, or pleiotropically, or both. A structured input-output lasso (SIOL) model based on an intricate l1/l2-norm penalty over the regression coefficient matrix is employed to enable discovery of complex sparse input/output relationships; and a highly efficient new optimization algorithm called hierarchical group thresholding (HiGT) is developed to solve the resultant non-differentiable, non-separable, and ultra high-dimensional optimization problem. We show on both simulation and on a yeast eQTL dataset that our model leads to significantly better recovery of the structured sparse relationships between the inputs and the outputs, and our algorithm significantly outperforms other optimization techniques under the same model. Additionally, we propose a novel approach for efficiently and effectively detecting input interactions by exploiting the prior knowledge available from biological experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge