Primitives for Dynamic Big Model Parallelism
Paper and Code
Jun 18, 2014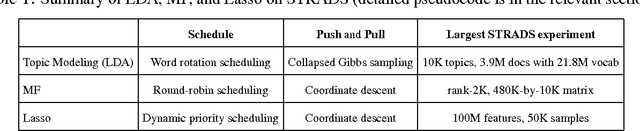
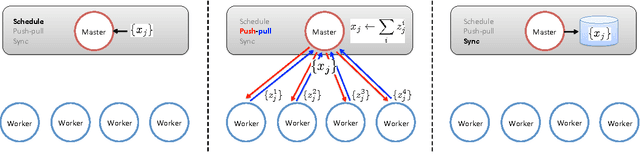

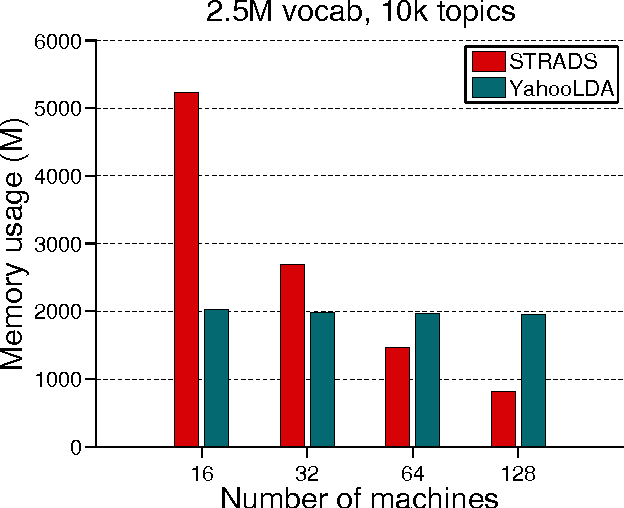
When training large machine learning models with many variables or parameters, a single machine is often inadequate since the model may be too large to fit in memory, while training can take a long time even with stochastic updates. A natural recourse is to turn to distributed cluster computing, in order to harness additional memory and processors. However, naive, unstructured parallelization of ML algorithms can make inefficient use of distributed memory, while failing to obtain proportional convergence speedups - or can even result in divergence. We develop a framework of primitives for dynamic model-parallelism, STRADS, in order to explore partitioning and update scheduling of model variables in distributed ML algorithms - thus improving their memory efficiency while presenting new opportunities to speed up convergence without compromising inference correctness. We demonstrate the efficacy of model-parallel algorithms implemented in STRADS versus popular implementations for Topic Modeling, Matrix Factorization and Lasso.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge