The Nonlinearity Coefficient -- A Practical Guide to Neural Architecture Design

In essence, a neural network is an arbitrary differentiable, parametrized function. Choosing a neural network architecture for any task is as complex as searching the space of those functions. For the last few years, 'neural architecture design' has been largely synonymous with 'neural architecture search' (NAS), i.e. brute-force, large-scale search. NAS has yielded significant gains on practical tasks. However, NAS methods end up searching for a local optimum in architecture space in a small neighborhood around architectures that often go back decades, based on CNN or LSTM. In this work, we present a different and complementary approach to architecture design, which we term 'zero-shot architecture design' (ZSAD). We develop methods that can predict, without any training, whether an architecture will achieve a relatively high test or training error on a task after training. We then go on to explain the error in terms of the architecture definition itself and develop tools for modifying the architecture based on this explanation. This confers an unprecedented level of control on the deep learning practitioner. They can make informed design decisions before the first line of code is written, even for tasks for which no prior art exists. Our first major contribution is to show that the 'degree of nonlinearity' of a neural architecture is a key causal driver behind its performance, and a primary aspect of the architecture's model complexity. We introduce the 'nonlinearity coefficient' (NLC), a scalar metric for measuring nonlinearity. Via extensive empirical study, we show that the value of the NLC in the architecture's randomly initialized state before training is a powerful predictor of test error after training and that attaining a right-sized NLC is essential for attaining an optimal test error. The NLC is also conceptually simple, well-defined for any feedforward network, easy and cheap to compute, has extensive theoretical, empirical and conceptual grounding, follows instructively from the architecture definition, and can be easily controlled via our 'nonlinearity normalization' algorithm. We argue that the NLC is the most powerful scalar statistic for architecture design specifically and neural network analysis in general. Our analysis is fueled by mean field theory, which we use to uncover the 'meta-distribution' of layers. Beyond the NLC, we uncover and flesh out a range of metrics and properties that have a significant explanatory influence on test and training error. We go on to explain the majority of the error variation across a wide range of randomly generated architectures with these metrics and properties. We compile our insights into a practical guide for architecture designers, which we argue can significantly shorten the trial-and-error phase of deep learning deployment. Our results are grounded in an experimental protocol that exceeds that of the vast majority of other deep learning studies in terms of carefulness and rigor. We study the impact of e.g. dataset, learning rate, floating-point precision, loss function, statistical estimation error and batch inter-dependency on performance and other key properties. We promote research practices that we believe can significantly accelerate progress in architecture design research.

The Nonlinearity Coefficient - Predicting Overfitting in Deep Neural Networks

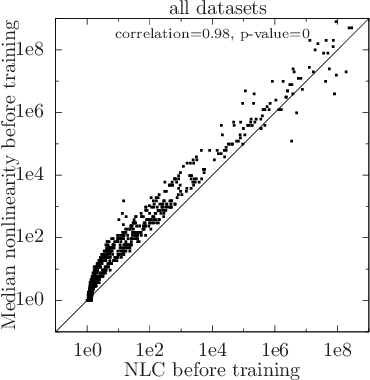
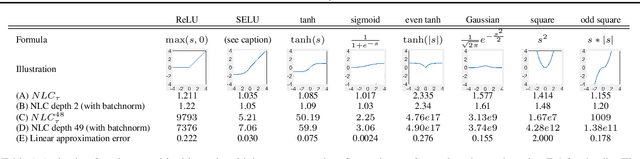
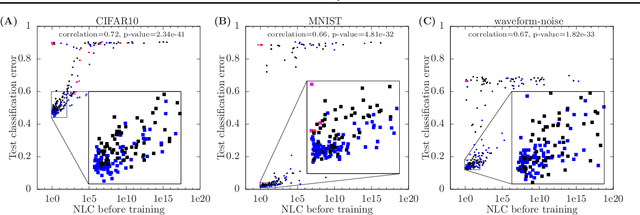
For a long time, designing neural architectures that exhibit high performance was considered a dark art that required expert hand-tuning. One of the few well-known guidelines for architecture design is the avoidance of exploding gradients, though even this guideline has remained relatively vague and circumstantial. We introduce the nonlinearity coefficient (NLC), a measurement of the complexity of the function computed by a neural network that is based on the magnitude of the gradient. Via an extensive empirical study, we show that the NLC is a powerful predictor of test error and that attaining a right-sized NLC is essential for optimal performance. The NLC exhibits a range of intriguing and important properties. It is closely tied to the amount of information gained from computing a single network gradient. It is tied to the error incurred when replacing the nonlinearity operations in the network with linear operations. It is not susceptible to the confounders of multiplicative scaling, additive bias and layer width. It is stable from layer to layer. Hence, we argue that the NLC is the first robust predictor of overfitting in deep networks.

The exploding gradient problem demystified - definition, prevalence, impact, origin, tradeoffs, and solutions

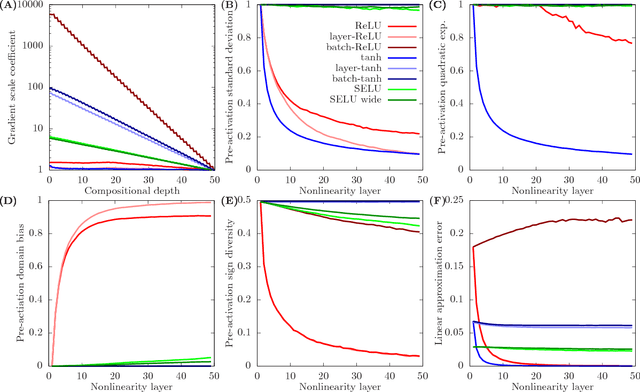
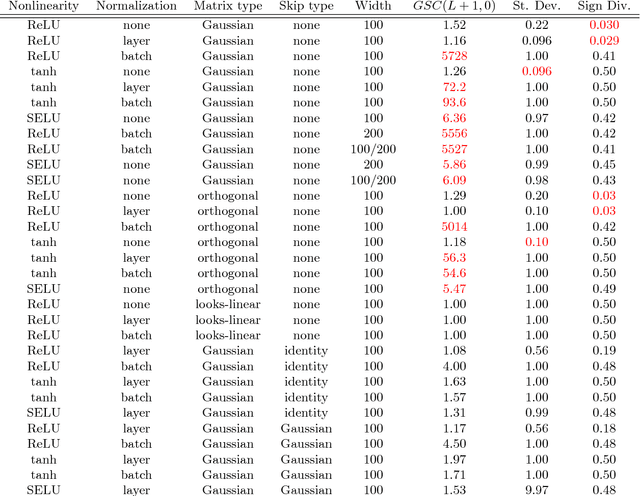
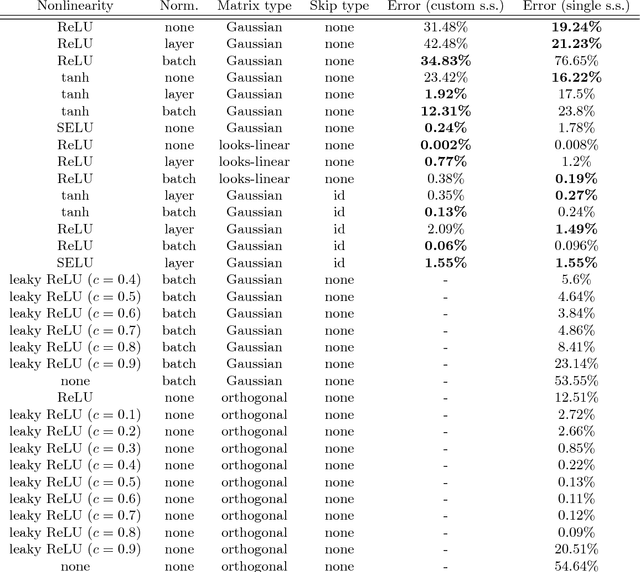
Whereas it is believed that techniques such as Adam, batch normalization and, more recently, SeLU nonlinearities "solve" the exploding gradient problem, we show that this is not the case in general and that in a range of popular MLP architectures, exploding gradients exist and that they limit the depth to which networks can be effectively trained, both in theory and in practice. We explain why exploding gradients occur and highlight the *collapsing domain problem*, which can arise in architectures that avoid exploding gradients. ResNets have significantly lower gradients and thus can circumvent the exploding gradient problem, enabling the effective training of much deeper networks. We show this is a direct consequence of the Pythagorean equation. By noticing that *any neural network is a residual network*, we devise the *residual trick*, which reveals that introducing skip connections simplifies the network mathematically, and that this simplicity may be the major cause for their success.

Nonparametric Neural Networks

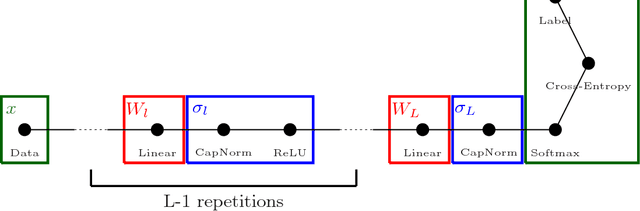
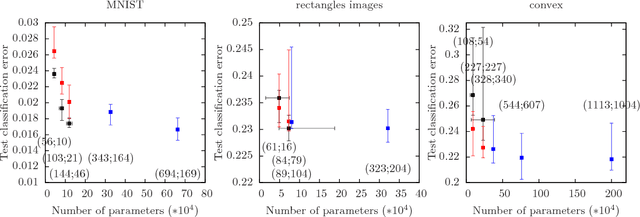
Automatically determining the optimal size of a neural network for a given task without prior information currently requires an expensive global search and training many networks from scratch. In this paper, we address the problem of automatically finding a good network size during a single training cycle. We introduce *nonparametric neural networks*, a non-probabilistic framework for conducting optimization over all possible network sizes and prove its soundness when network growth is limited via an L_p penalty. We train networks under this framework by continuously adding new units while eliminating redundant units via an L_2 penalty. We employ a novel optimization algorithm, which we term *adaptive radial-angular gradient descent* or *AdaRad*, and obtain promising results.

Stability Selection for Structured Variable Selection

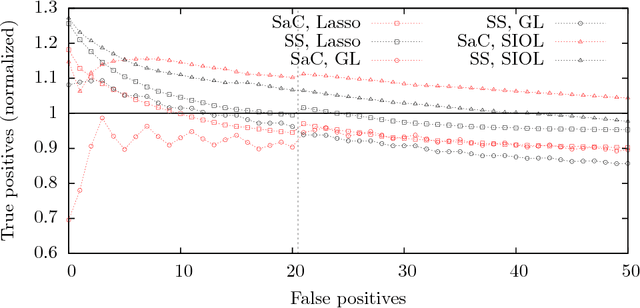
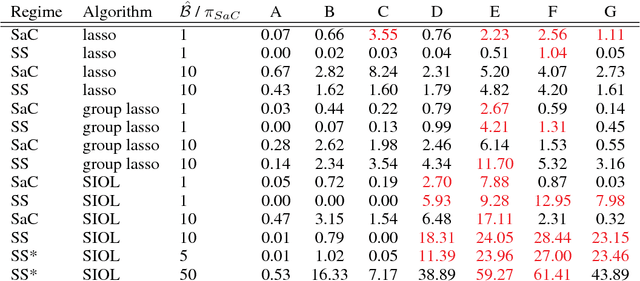
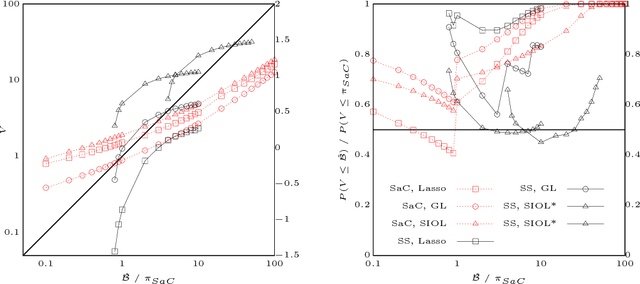
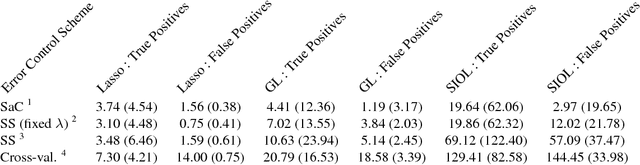
In variable or graph selection problems, finding a right-sized model or controlling the number of false positives is notoriously difficult. Recently, a meta-algorithm called Stability Selection was proposed that can provide reliable finite-sample control of the number of false positives. Its benefits were demonstrated when used in conjunction with the lasso and orthogonal matching pursuit algorithms. In this paper, we investigate the applicability of stability selection to structured selection algorithms: the group lasso and the structured input-output lasso. We find that using stability selection often increases the power of both algorithms, but that the presence of complex structure reduces the reliability of error control under stability selection. We give strategies for setting tuning parameters to obtain a good model size under stability selection, and highlight its strengths and weaknesses compared to competing methods screen and clean and cross-validation. We give guidelines about when to use which error control method.