The Nonlinearity Coefficient - Predicting Overfitting in Deep Neural Networks

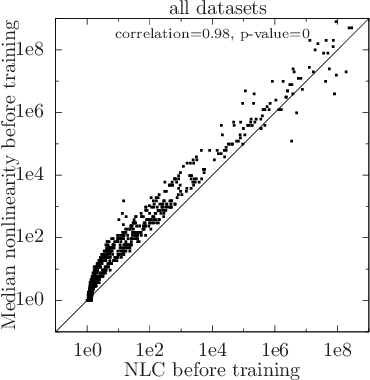
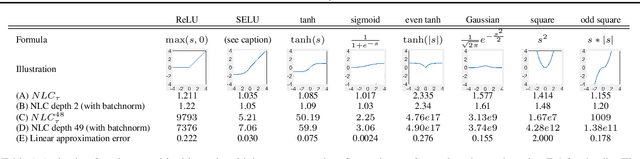
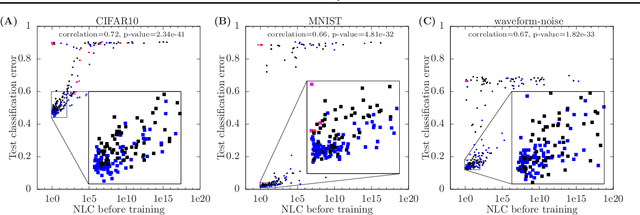
For a long time, designing neural architectures that exhibit high performance was considered a dark art that required expert hand-tuning. One of the few well-known guidelines for architecture design is the avoidance of exploding gradients, though even this guideline has remained relatively vague and circumstantial. We introduce the nonlinearity coefficient (NLC), a measurement of the complexity of the function computed by a neural network that is based on the magnitude of the gradient. Via an extensive empirical study, we show that the NLC is a powerful predictor of test error and that attaining a right-sized NLC is essential for optimal performance. The NLC exhibits a range of intriguing and important properties. It is closely tied to the amount of information gained from computing a single network gradient. It is tied to the error incurred when replacing the nonlinearity operations in the network with linear operations. It is not susceptible to the confounders of multiplicative scaling, additive bias and layer width. It is stable from layer to layer. Hence, we argue that the NLC is the first robust predictor of overfitting in deep networks.