The exploding gradient problem demystified - definition, prevalence, impact, origin, tradeoffs, and solutions
Paper and Code
Apr 06, 2018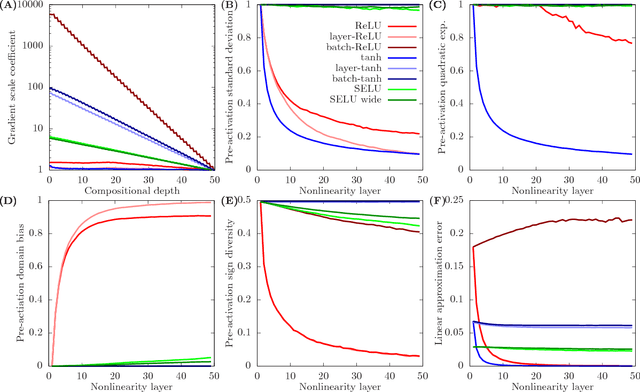
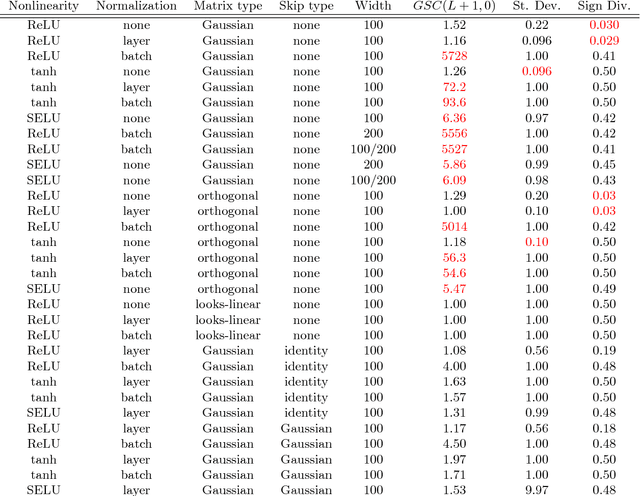

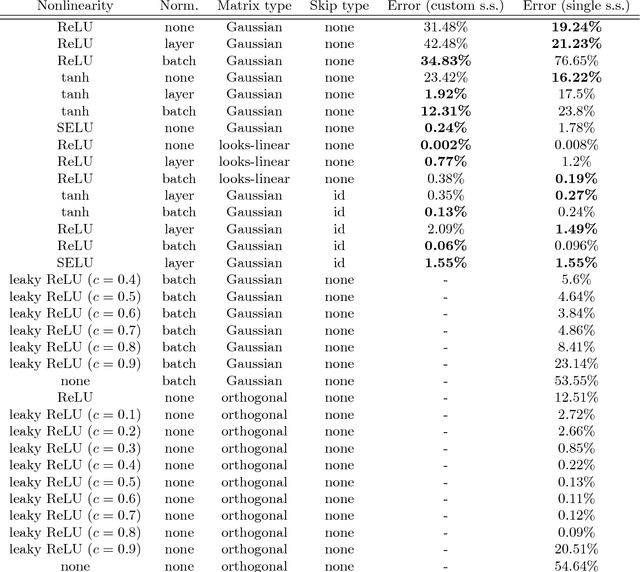
Whereas it is believed that techniques such as Adam, batch normalization and, more recently, SeLU nonlinearities "solve" the exploding gradient problem, we show that this is not the case in general and that in a range of popular MLP architectures, exploding gradients exist and that they limit the depth to which networks can be effectively trained, both in theory and in practice. We explain why exploding gradients occur and highlight the *collapsing domain problem*, which can arise in architectures that avoid exploding gradients. ResNets have significantly lower gradients and thus can circumvent the exploding gradient problem, enabling the effective training of much deeper networks. We show this is a direct consequence of the Pythagorean equation. By noticing that *any neural network is a residual network*, we devise the *residual trick*, which reveals that introducing skip connections simplifies the network mathematically, and that this simplicity may be the major cause for their success.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge