Nonparametric Neural Networks
Paper and Code
Dec 14, 2017
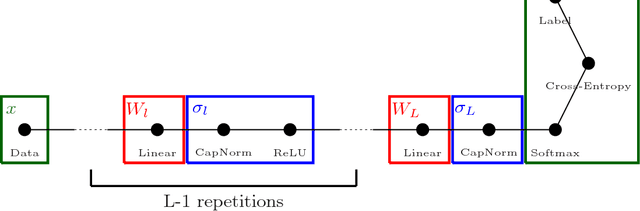
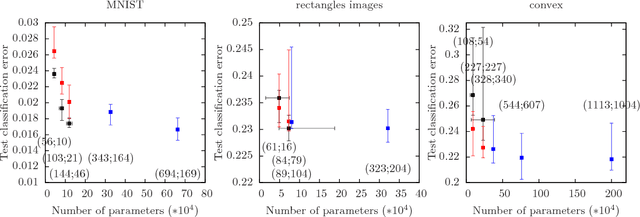

Automatically determining the optimal size of a neural network for a given task without prior information currently requires an expensive global search and training many networks from scratch. In this paper, we address the problem of automatically finding a good network size during a single training cycle. We introduce *nonparametric neural networks*, a non-probabilistic framework for conducting optimization over all possible network sizes and prove its soundness when network growth is limited via an L_p penalty. We train networks under this framework by continuously adding new units while eliminating redundant units via an L_2 penalty. We employ a novel optimization algorithm, which we term *adaptive radial-angular gradient descent* or *AdaRad*, and obtain promising results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge