Stability Selection for Structured Variable Selection
Paper and Code
Dec 13, 2017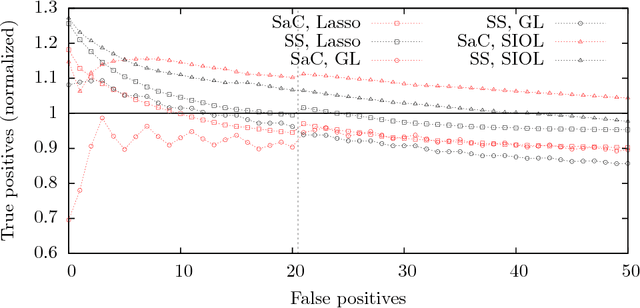
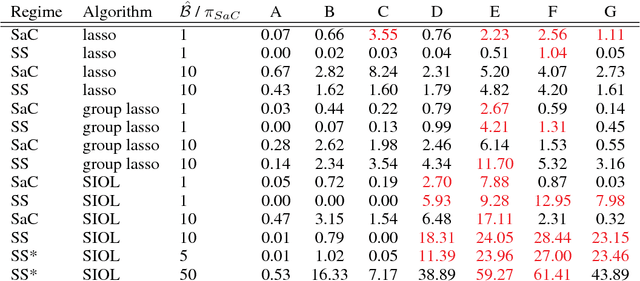
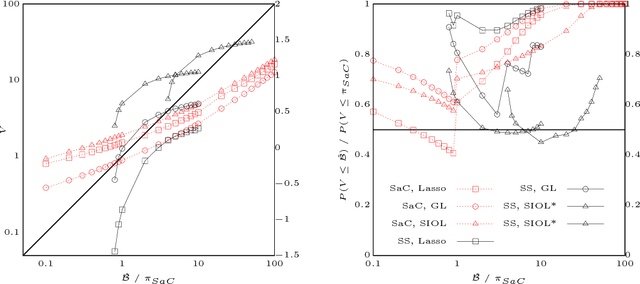
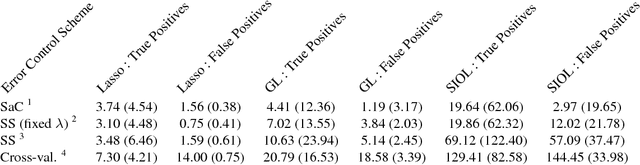
In variable or graph selection problems, finding a right-sized model or controlling the number of false positives is notoriously difficult. Recently, a meta-algorithm called Stability Selection was proposed that can provide reliable finite-sample control of the number of false positives. Its benefits were demonstrated when used in conjunction with the lasso and orthogonal matching pursuit algorithms. In this paper, we investigate the applicability of stability selection to structured selection algorithms: the group lasso and the structured input-output lasso. We find that using stability selection often increases the power of both algorithms, but that the presence of complex structure reduces the reliability of error control under stability selection. We give strategies for setting tuning parameters to obtain a good model size under stability selection, and highlight its strengths and weaknesses compared to competing methods screen and clean and cross-validation. We give guidelines about when to use which error control method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge