Structure-Aware Dynamic Scheduler for Parallel Machine Learning
Paper and Code
Dec 30, 2013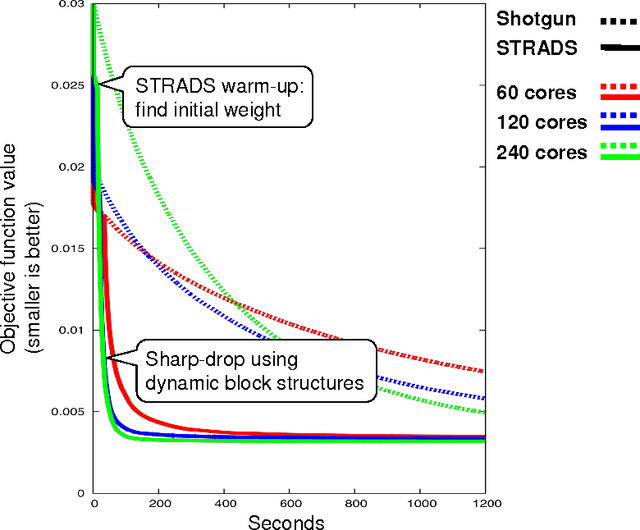
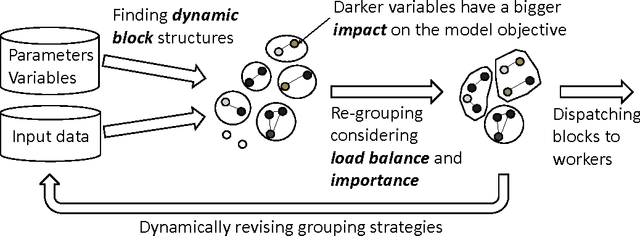
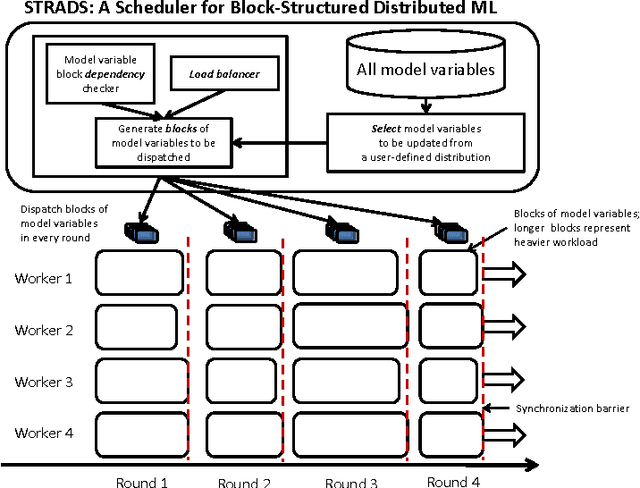
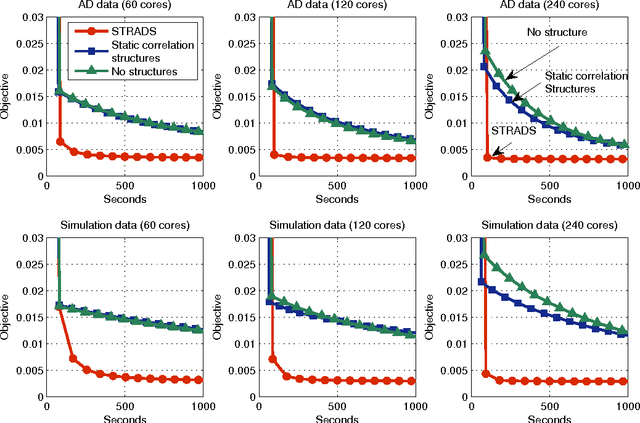
Training large machine learning (ML) models with many variables or parameters can take a long time if one employs sequential procedures even with stochastic updates. A natural solution is to turn to distributed computing on a cluster; however, naive, unstructured parallelization of ML algorithms does not usually lead to a proportional speedup and can even result in divergence, because dependencies between model elements can attenuate the computational gains from parallelization and compromise correctness of inference. Recent efforts toward this issue have benefited from exploiting the static, a priori block structures residing in ML algorithms. In this paper, we take this path further by exploring the dynamic block structures and workloads therein present during ML program execution, which offers new opportunities for improving convergence, correctness, and load balancing in distributed ML. We propose and showcase a general-purpose scheduler, STRADS, for coordinating distributed updates in ML algorithms, which harnesses the aforementioned opportunities in a systematic way. We provide theoretical guarantees for our scheduler, and demonstrate its efficacy versus static block structures on Lasso and Matrix Factorization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge