Distributed Machine Learning via Sufficient Factor Broadcasting
Paper and Code
Nov 26, 2015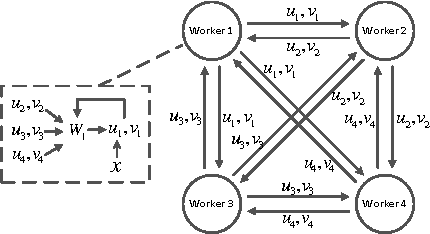
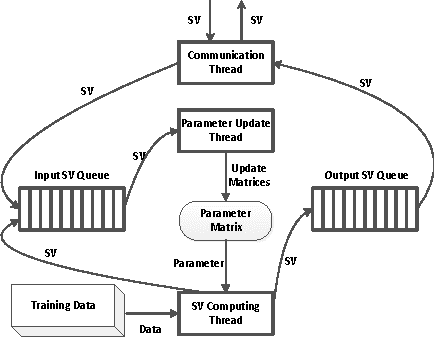


Matrix-parametrized models, including multiclass logistic regression and sparse coding, are used in machine learning (ML) applications ranging from computer vision to computational biology. When these models are applied to large-scale ML problems starting at millions of samples and tens of thousands of classes, their parameter matrix can grow at an unexpected rate, resulting in high parameter synchronization costs that greatly slow down distributed learning. To address this issue, we propose a Sufficient Factor Broadcasting (SFB) computation model for efficient distributed learning of a large family of matrix-parameterized models, which share the following property: the parameter update computed on each data sample is a rank-1 matrix, i.e., the outer product of two "sufficient factors" (SFs). By broadcasting the SFs among worker machines and reconstructing the update matrices locally at each worker, SFB improves communication efficiency --- communication costs are linear in the parameter matrix's dimensions, rather than quadratic --- without affecting computational correctness. We present a theoretical convergence analysis of SFB, and empirically corroborate its efficiency on four different matrix-parametrized ML models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge