Alexander J Smola
IRLI: Iterative Re-partitioning for Learning to Index
Mar 17, 2021



Abstract:Neural models have transformed the fundamental information retrieval problem of mapping a query to a giant set of items. However, the need for efficient and low latency inference forces the community to reconsider efficient approximate near-neighbor search in the item space. To this end, learning to index is gaining much interest in recent times. Methods have to trade between obtaining high accuracy while maintaining load balance and scalability in distributed settings. We propose a novel approach called IRLI (pronounced `early'), which iteratively partitions the items by learning the relevant buckets directly from the query-item relevance data. Furthermore, IRLI employs a superior power-of-$k$-choices based load balancing strategy. We mathematically show that IRLI retrieves the correct item with high probability under very natural assumptions and provides superior load balancing. IRLI surpasses the best baseline's precision on multi-label classification while being $5x$ faster on inference. For near-neighbor search tasks, the same method outperforms the state-of-the-art Learned Hashing approach NeuralLSH by requiring only ~ {1/6}^th of the candidates for the same recall. IRLI is both data and model parallel, making it ideal for distributed GPU implementation. We demonstrate this advantage by indexing 100 million dense vectors and surpassing the popular FAISS library by >10% on recall.
State Space LSTM Models with Particle MCMC Inference
Nov 30, 2017



Abstract:Long Short-Term Memory (LSTM) is one of the most powerful sequence models. Despite the strong performance, however, it lacks the nice interpretability as in state space models. In this paper, we present a way to combine the best of both worlds by introducing State Space LSTM (SSL) models that generalizes the earlier work \cite{zaheer2017latent} of combining topic models with LSTM. However, unlike \cite{zaheer2017latent}, we do not make any factorization assumptions in our inference algorithm. We present an efficient sampler based on sequential Monte Carlo (SMC) method that draws from the joint posterior directly. Experimental results confirms the superiority and stability of this SMC inference algorithm on a variety of domains.
A Generic Approach for Escaping Saddle points
Sep 05, 2017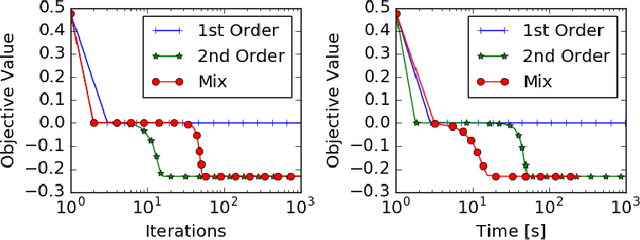
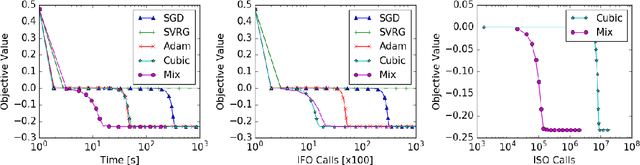

Abstract:A central challenge to using first-order methods for optimizing nonconvex problems is the presence of saddle points. First-order methods often get stuck at saddle points, greatly deteriorating their performance. Typically, to escape from saddles one has to use second-order methods. However, most works on second-order methods rely extensively on expensive Hessian-based computations, making them impractical in large-scale settings. To tackle this challenge, we introduce a generic framework that minimizes Hessian based computations while at the same time provably converging to second-order critical points. Our framework carefully alternates between a first-order and a second-order subroutine, using the latter only close to saddle points, and yields convergence results competitive to the state-of-the-art. Empirical results suggest that our strategy also enjoys a good practical performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge