Sashank J Reddi
Why ADAM Beats SGD for Attention Models
Dec 06, 2019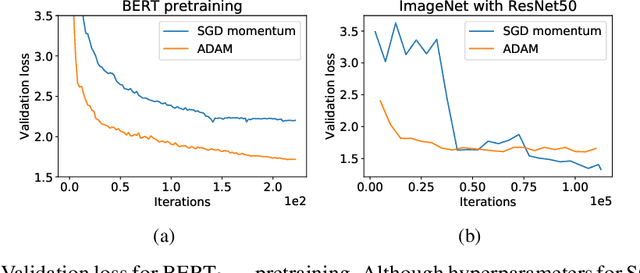

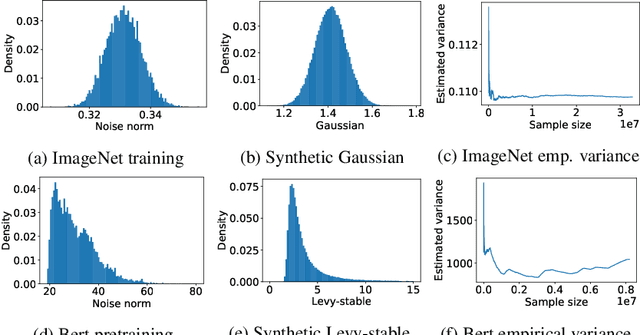

Abstract:While stochastic gradient descent (SGD) is still the de facto algorithm in deep learning, adaptive methods like Adam have been observed to outperform SGD across important tasks, such as attention models. The settings under which SGD performs poorly in comparison to Adam are not well understood yet. In this paper, we provide empirical and theoretical evidence that a heavy-tailed distribution of the noise in stochastic gradients is a root cause of SGD's poor performance. Based on this observation, we study clipped variants of SGD that circumvent this issue; we then analyze their convergence under heavy-tailed noise. Furthermore, we develop a new adaptive coordinate-wise clipping algorithm (ACClip) tailored to such settings. Subsequently, we show how adaptive methods like Adam can be viewed through the lens of clipping, which helps us explain Adam's strong performance under heavy-tail noise settings. Finally, we show that the proposed ACClip outperforms Adam for both BERT pretraining and finetuning tasks.
A Generic Approach for Escaping Saddle points
Sep 05, 2017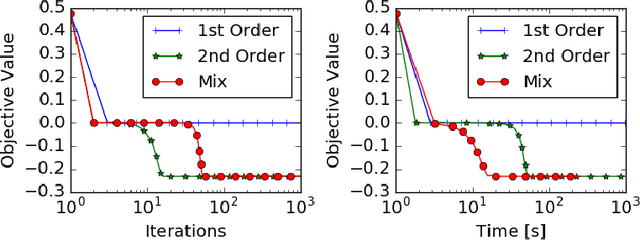
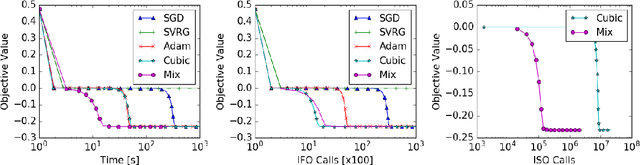

Abstract:A central challenge to using first-order methods for optimizing nonconvex problems is the presence of saddle points. First-order methods often get stuck at saddle points, greatly deteriorating their performance. Typically, to escape from saddles one has to use second-order methods. However, most works on second-order methods rely extensively on expensive Hessian-based computations, making them impractical in large-scale settings. To tackle this challenge, we introduce a generic framework that minimizes Hessian based computations while at the same time provably converging to second-order critical points. Our framework carefully alternates between a first-order and a second-order subroutine, using the latter only close to saddle points, and yields convergence results competitive to the state-of-the-art. Empirical results suggest that our strategy also enjoys a good practical performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge