Learning Tensor Latent Features
Paper and Code
Oct 10, 2018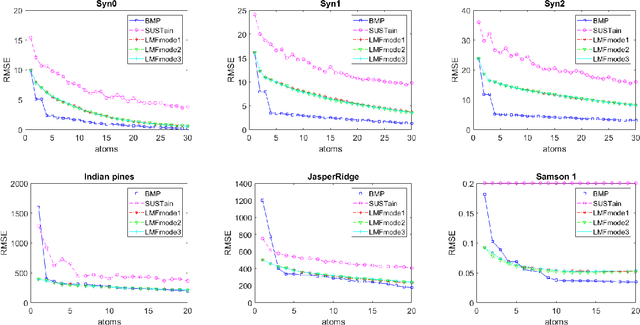
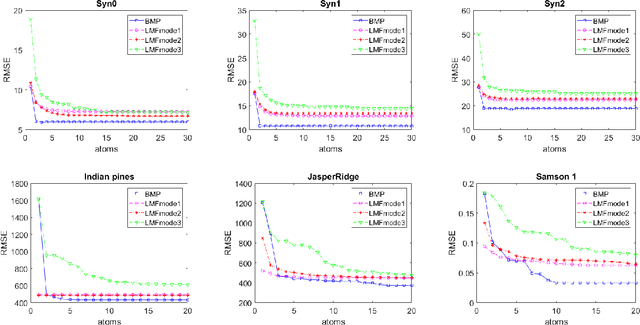
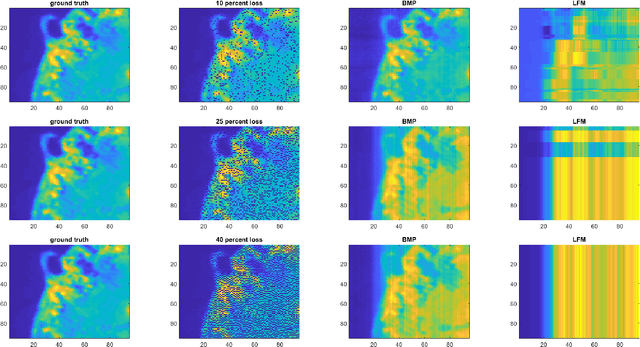
We study the problem of learning latent feature models (LFMs) for tensor data commonly observed in science and engineering such as hyperspectral imagery. However, the problem is challenging not only due to the non-convex formulation, the combinatorial nature of the constraints in LFMs, but also the high-order correlations in the data. In this work, we formulate a tensor latent feature learning problem by representing the data as a mixture of high-order latent features and binary codes, which are memory efficient and easy to interpret. To make the learning tractable, we propose a novel optimization procedure, Binary matching pursuit (BMP), that iteratively searches for binary bases via a MAXCUT-like boolean quadratic solver. Such a procedure is guaranteed to achieve an? suboptimal solution in O($1/\epsilon$) greedy steps, resulting in a trade-off between accuracy and sparsity. When evaluated on both synthetic and real datasets, our experiments show superior performance over baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge