Ian E. H. Yen
Sparse Progressive Distillation: Resolving Overfitting under Pretrain-and-Finetune Paradigm
Oct 18, 2021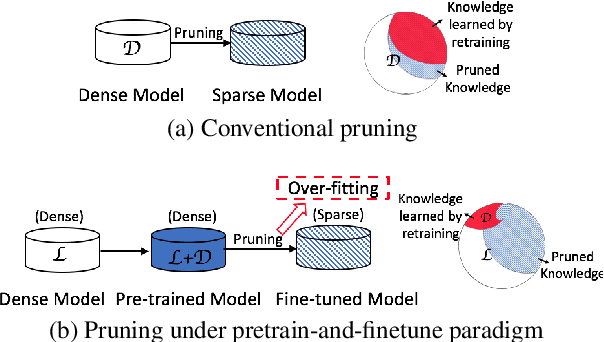
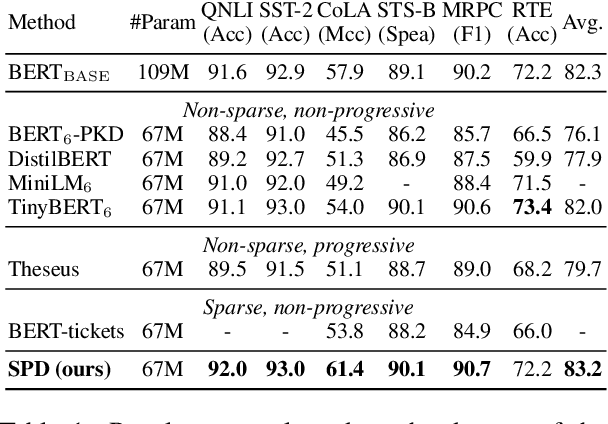
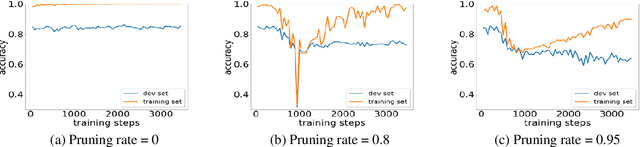
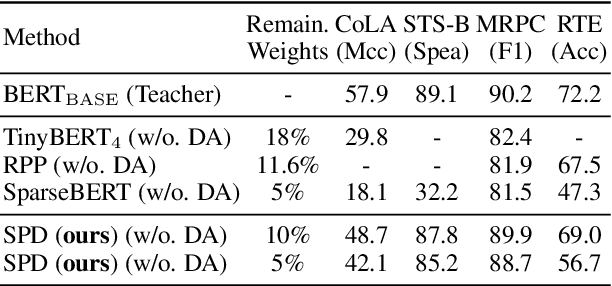
Abstract:Various pruning approaches have been proposed to reduce the footprint requirements of Transformer-based language models. Conventional wisdom is that pruning reduces the model expressiveness and thus is more likely to underfit than overfit compared to the original model. However, under the trending pretrain-and-finetune paradigm, we argue that pruning increases the risk of overfitting if pruning was performed at the fine-tuning phase, as it increases the amount of information a model needs to learn from the downstream task, resulting in relative data deficiency. In this paper, we aim to address the overfitting issue under the pretrain-and-finetune paradigm to improve pruning performance via progressive knowledge distillation (KD) and sparse pruning. Furthermore, to mitigate the interference between different strategies of learning rate, pruning and distillation, we propose a three-stage learning framework. We show for the first time that reducing the risk of overfitting can help the effectiveness of pruning under the pretrain-and-finetune paradigm. Experiments on multiple datasets of GLUE benchmark show that our method achieves highly competitive pruning performance over the state-of-the-art competitors across different pruning ratio constraints.
Rethinking Network Pruning -- under the Pre-train and Fine-tune Paradigm
Apr 18, 2021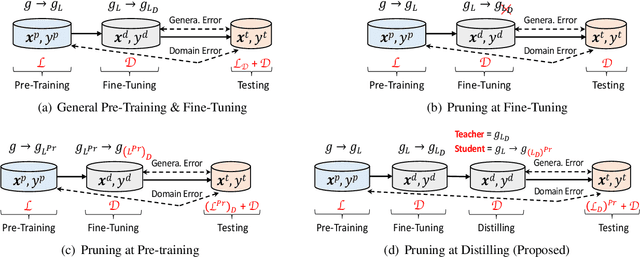
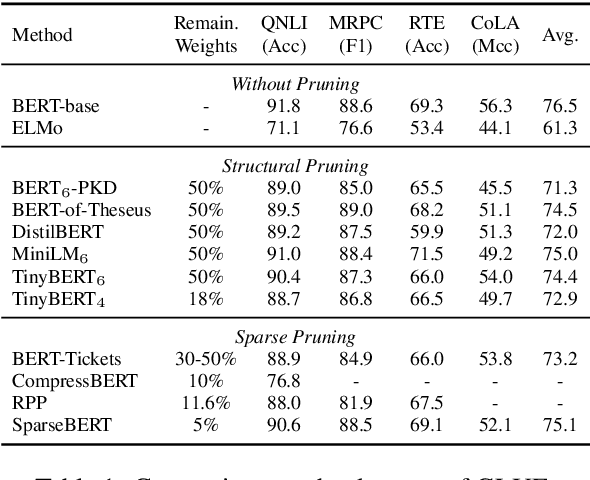
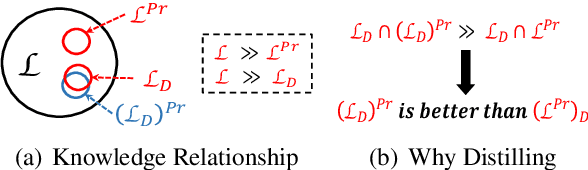
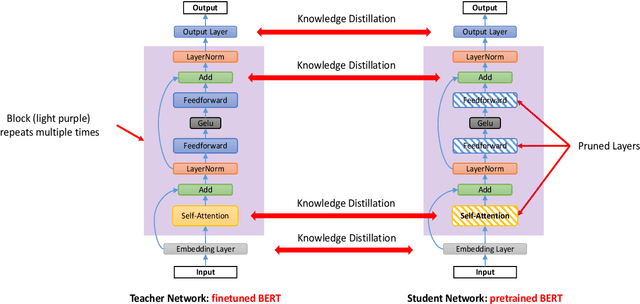
Abstract:Transformer-based pre-trained language models have significantly improved the performance of various natural language processing (NLP) tasks in the recent years. While effective and prevalent, these models are usually prohibitively large for resource-limited deployment scenarios. A thread of research has thus been working on applying network pruning techniques under the pretrain-then-finetune paradigm widely adopted in NLP. However, the existing pruning results on benchmark transformers, such as BERT, are not as remarkable as the pruning results in the literature of convolutional neural networks (CNNs). In particular, common wisdom in pruning CNN states that sparse pruning technique compresses a model more than that obtained by reducing number of channels and layers (Elsen et al., 2020; Zhu and Gupta, 2017), while existing works on sparse pruning of BERT yields inferior results than its small-dense counterparts such as TinyBERT (Jiao et al., 2020). In this work, we aim to fill this gap by studying how knowledge are transferred and lost during the pre-train, fine-tune, and pruning process, and proposing a knowledge-aware sparse pruning process that achieves significantly superior results than existing literature. We show for the first time that sparse pruning compresses a BERT model significantly more than reducing its number of channels and layers. Experiments on multiple data sets of GLUE benchmark show that our method outperforms the leading competitors with a 20-times weight/FLOPs compression and neglectable loss in prediction accuracy.
Minimizing FLOPs to Learn Efficient Sparse Representations
Apr 12, 2020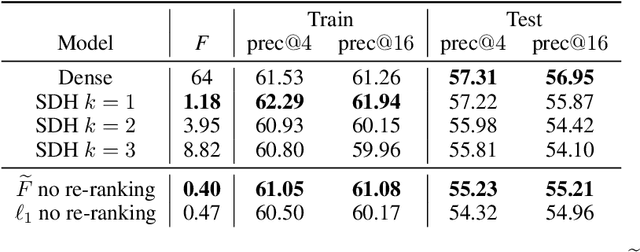

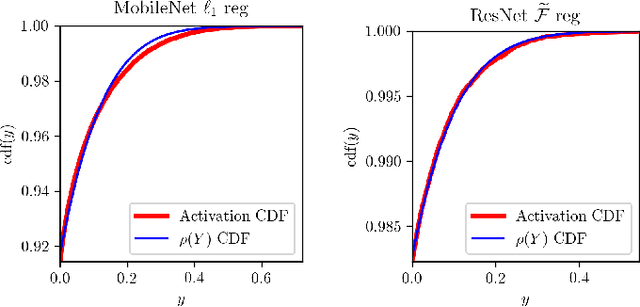
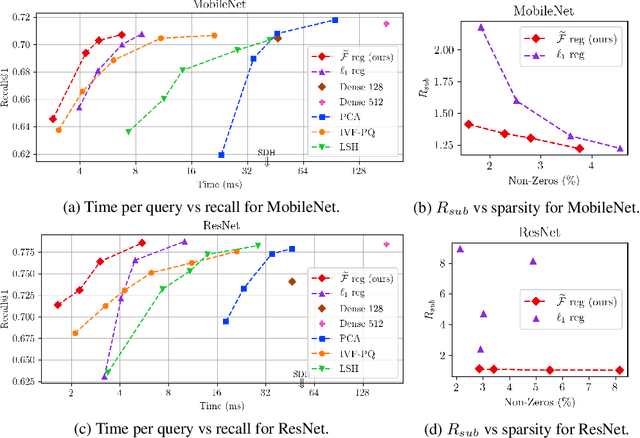
Abstract:Deep representation learning has become one of the most widely adopted approaches for visual search, recommendation, and identification. Retrieval of such representations from a large database is however computationally challenging. Approximate methods based on learning compact representations, have been widely explored for this problem, such as locality sensitive hashing, product quantization, and PCA. In this work, in contrast to learning compact representations, we propose to learn high dimensional and sparse representations that have similar representational capacity as dense embeddings while being more efficient due to sparse matrix multiplication operations which can be much faster than dense multiplication. Following the key insight that the number of operations decreases quadratically with the sparsity of embeddings provided the non-zero entries are distributed uniformly across dimensions, we propose a novel approach to learn such distributed sparse embeddings via the use of a carefully constructed regularization function that directly minimizes a continuous relaxation of the number of floating-point operations (FLOPs) incurred during retrieval. Our experiments show that our approach is competitive to the other baselines and yields a similar or better speed-vs-accuracy tradeoff on practical datasets.
Representer Point Selection for Explaining Deep Neural Networks
Nov 23, 2018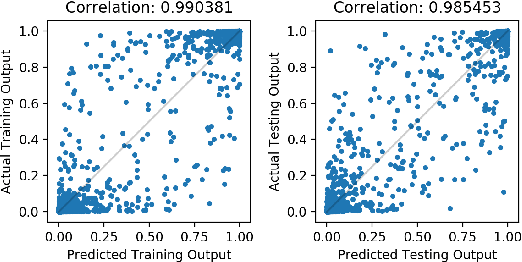

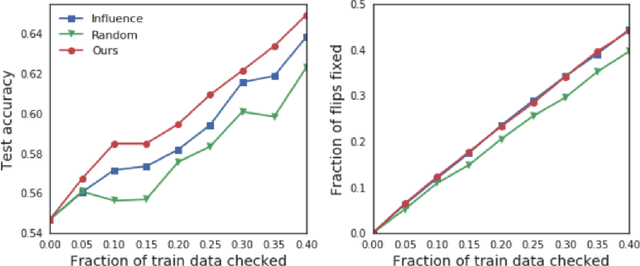

Abstract:We propose to explain the predictions of a deep neural network, by pointing to the set of what we call representer points in the training set, for a given test point prediction. Specifically, we show that we can decompose the pre-activation prediction of a neural network into a linear combination of activations of training points, with the weights corresponding to what we call representer values, which thus capture the importance of that training point on the learned parameters of the network. But it provides a deeper understanding of the network than simply training point influence: with positive representer values corresponding to excitatory training points, and negative values corresponding to inhibitory points, which as we show provides considerably more insight. Our method is also much more scalable, allowing for real-time feedback in a manner not feasible with influence functions.
Word Mover's Embedding: From Word2Vec to Document Embedding
Oct 30, 2018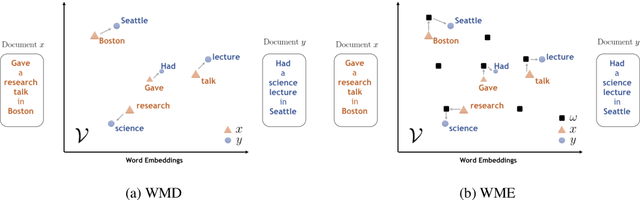
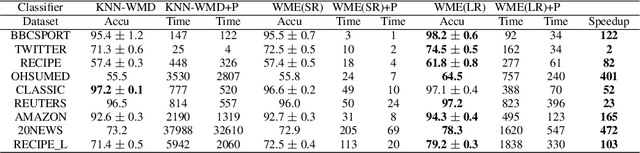
Abstract:While the celebrated Word2Vec technique yields semantically rich representations for individual words, there has been relatively less success in extending to generate unsupervised sentences or documents embeddings. Recent work has demonstrated that a distance measure between documents called \emph{Word Mover's Distance} (WMD) that aligns semantically similar words, yields unprecedented KNN classification accuracy. However, WMD is expensive to compute, and it is hard to extend its use beyond a KNN classifier. In this paper, we propose the \emph{Word Mover's Embedding } (WME), a novel approach to building an unsupervised document (sentence) embedding from pre-trained word embeddings. In our experiments on 9 benchmark text classification datasets and 22 textual similarity tasks, the proposed technique consistently matches or outperforms state-of-the-art techniques, with significantly higher accuracy on problems of short length.
Learning Tensor Latent Features
Oct 10, 2018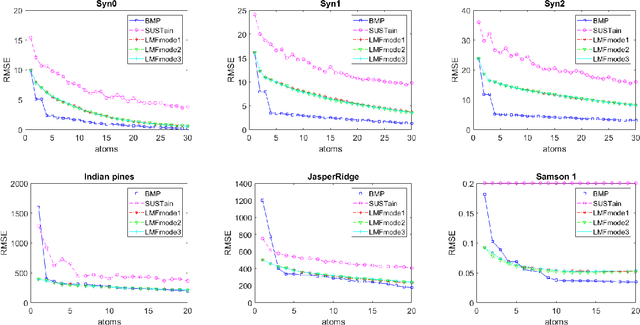
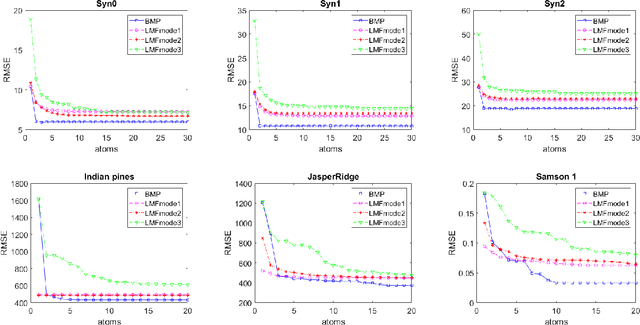
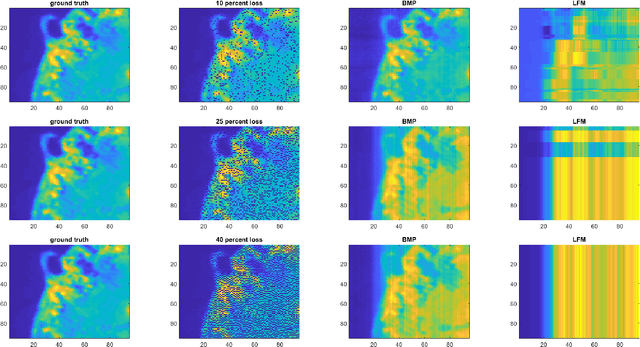
Abstract:We study the problem of learning latent feature models (LFMs) for tensor data commonly observed in science and engineering such as hyperspectral imagery. However, the problem is challenging not only due to the non-convex formulation, the combinatorial nature of the constraints in LFMs, but also the high-order correlations in the data. In this work, we formulate a tensor latent feature learning problem by representing the data as a mixture of high-order latent features and binary codes, which are memory efficient and easy to interpret. To make the learning tractable, we propose a novel optimization procedure, Binary matching pursuit (BMP), that iteratively searches for binary bases via a MAXCUT-like boolean quadratic solver. Such a procedure is guaranteed to achieve an? suboptimal solution in O($1/\epsilon$) greedy steps, resulting in a trade-off between accuracy and sparsity. When evaluated on both synthetic and real datasets, our experiments show superior performance over baseline methods.
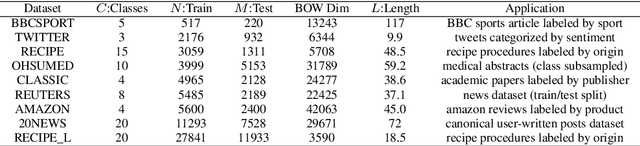
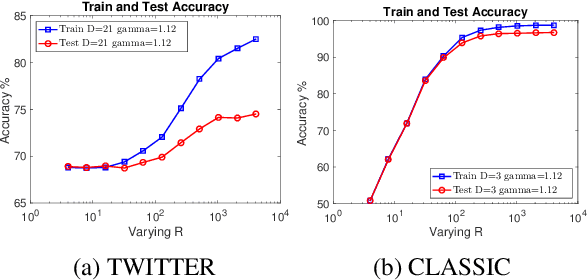
Revisiting Random Binning Features: Fast Convergence and Strong Parallelizability
Sep 19, 2018
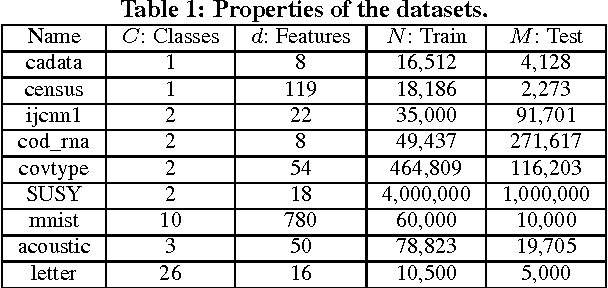
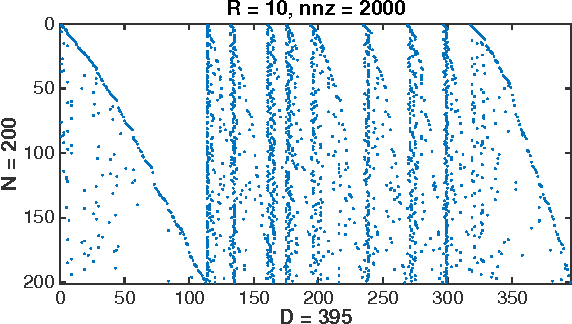
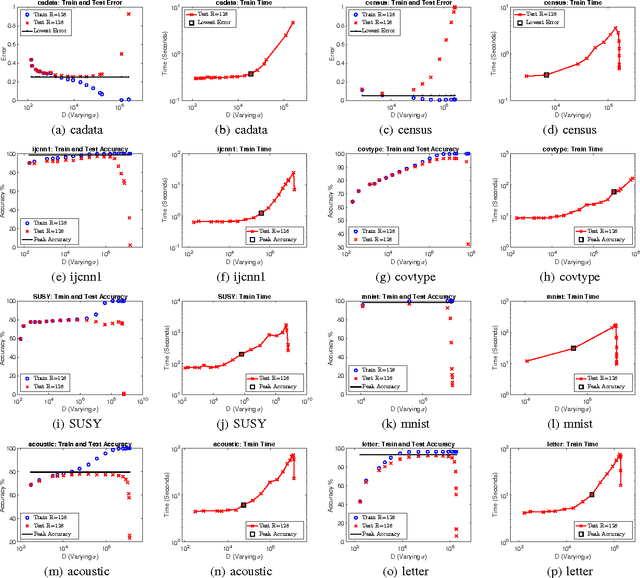
Abstract:Kernel method has been developed as one of the standard approaches for nonlinear learning, which however, does not scale to large data set due to its quadratic complexity in the number of samples. A number of kernel approximation methods have thus been proposed in the recent years, among which the random features method gains much popularity due to its simplicity and direct reduction of nonlinear problem to a linear one. The Random Binning (RB) feature, proposed in the first random-feature paper \cite{rahimi2007random}, has drawn much less attention than the Random Fourier (RF) feature. In this work, we observe that the RB features, with right choice of optimization solver, could be orders-of-magnitude more efficient than other random features and kernel approximation methods under the same requirement of accuracy. We thus propose the first analysis of RB from the perspective of optimization, which by interpreting RB as a Randomized Block Coordinate Descent in the infinite-dimensional space, gives a faster convergence rate compared to that of other random features. In particular, we show that by drawing $R$ random grids with at least $\kappa$ number of non-empty bins per grid in expectation, RB method achieves a convergence rate of $O(1/(\kappa R))$, which not only sharpens its $O(1/\sqrt{R})$ rate from Monte Carlo analysis, but also shows a $\kappa$ times speedup over other random features under the same analysis framework. In addition, we demonstrate another advantage of RB in the L1-regularized setting, where unlike other random features, a RB-based Coordinate Descent solver can be parallelized with guaranteed speedup proportional to $\kappa$. Our extensive experiments demonstrate the superior performance of the RB features over other random features and kernel approximation methods. Our code and data is available at { \url{https://github.com/teddylfwu/RB_GEN}}.
Proximal Quasi-Newton for Computationally Intensive L1-regularized M-estimators
Jan 23, 2015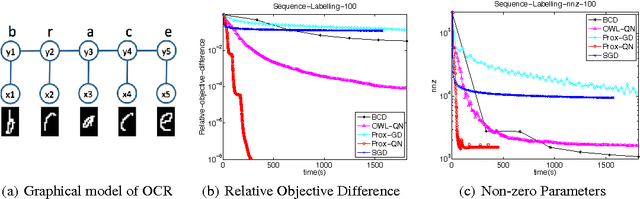
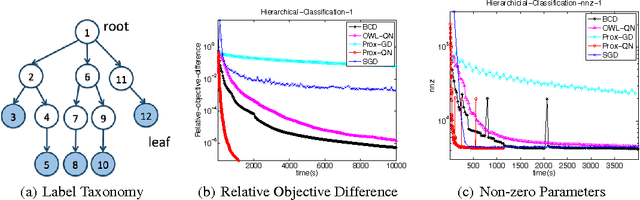
Abstract:We consider the class of optimization problems arising from computationally intensive L1-regularized M-estimators, where the function or gradient values are very expensive to compute. A particular instance of interest is the L1-regularized MLE for learning Conditional Random Fields (CRFs), which are a popular class of statistical models for varied structured prediction problems such as sequence labeling, alignment, and classification with label taxonomy. L1-regularized MLEs for CRFs are particularly expensive to optimize since computing the gradient values requires an expensive inference step. In this work, we propose the use of a carefully constructed proximal quasi-Newton algorithm for such computationally intensive M-estimation problems, where we employ an aggressive active set selection technique. In a key contribution of the paper, we show that the proximal quasi-Newton method is provably super-linearly convergent, even in the absence of strong convexity, by leveraging a restricted variant of strong convexity. In our experiments, the proposed algorithm converges considerably faster than current state-of-the-art on the problems of sequence labeling and hierarchical classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge