Marco-Bench-MIF: On Multilingual Instruction-Following Capability of Large Language Models

Instruction-following capability has become a major ability to be evaluated for Large Language Models (LLMs). However, existing datasets, such as IFEval, are either predominantly monolingual and centered on English or simply machine translated to other languages, limiting their applicability in multilingual contexts. In this paper, we present an carefully-curated extension of IFEval to a localized multilingual version named Marco-Bench-MIF, covering 30 languages with varying levels of localization. Our benchmark addresses linguistic constraints (e.g., modifying capitalization requirements for Chinese) and cultural references (e.g., substituting region-specific company names in prompts) via a hybrid pipeline combining translation with verification. Through comprehensive evaluation of 20+ LLMs on our Marco-Bench-MIF, we found that: (1) 25-35% accuracy gap between high/low-resource languages, (2) model scales largely impact performance by 45-60% yet persists script-specific challenges, and (3) machine-translated data underestimates accuracy by7-22% versus localized data. Our analysis identifies challenges in multilingual instruction following, including keyword consistency preservation and compositional constraint adherence across languages. Our Marco-Bench-MIF is available at https://github.com/AIDC-AI/Marco-Bench-MIF.

RODS: Robust Optimization Inspired Diffusion Sampling for Detecting and Reducing Hallucination in Generative Models

Diffusion models have achieved state-of-the-art performance in generative modeling, yet their sampling procedures remain vulnerable to hallucinations, often stemming from inaccuracies in score approximation. In this work, we reinterpret diffusion sampling through the lens of optimization and introduce RODS (Robust Optimization-inspired Diffusion Sampler), a novel method that detects and corrects high-risk sampling steps using geometric cues from the loss landscape. RODS enforces smoother sampling trajectories and adaptively adjusts perturbations, reducing hallucinations without retraining and at minimal additional inference cost. Experiments on AFHQv2, FFHQ, and 11k-hands demonstrate that RODS improves both sampling fidelity and robustness, detecting over 70% of hallucinated samples and correcting more than 25%, all while avoiding the introduction of new artifacts.

Towards Widening The Distillation Bottleneck for Reasoning Models

Large Reasoning Models(LRMs) such as OpenAI o1 and DeepSeek-R1 have shown remarkable reasoning capabilities by scaling test-time compute and generating long Chain-of-Thought(CoT). Distillation--post-training on LRMs-generated data--is a straightforward yet effective method to enhance the reasoning abilities of smaller models, but faces a critical bottleneck: we found that distilled long CoT data poses learning difficulty for small models and leads to the inheritance of biases (i.e. over-thinking) when using Supervised Fine-tuning(SFT) and Reinforcement Learning(RL) methods. To alleviate this bottleneck, we propose constructing tree-based CoT data from scratch via Monte Carlo Tree Search(MCTS). We then exploit a set of CoT-aware approaches, including Thoughts Length Balance, Fine-grained DPO, and Joint Post-training Objective, to enhance SFT and RL on the construted data.

Marco-LLM: Bridging Languages via Massive Multilingual Training for Cross-Lingual Enhancement

Large Language Models (LLMs) have achieved remarkable progress in recent years; however, their excellent performance is still largely limited to major world languages, primarily English. Many LLMs continue to face challenges with multilingual tasks, especially when it comes to low-resource languages. To address this issue, we introduced Marco-LLM: Massive multilingual training for cross-lingual enhancement LLM. We have collected a substantial amount of multilingual data for several low-resource languages and conducted extensive continual pre-training using the Qwen2 models. This effort has resulted in a multilingual LLM named Marco-LLM. Through comprehensive evaluations on various multilingual benchmarks, including MMMLU, AGIEval, Belebele, Flores-200, XCOPA and many others, Marco-LLM has demonstrated substantial improvements over state-of-the-art LLMs. Furthermore, Marco-LLM achieved substantial enhancements in any-to-any machine translation tasks, showing the effectiveness of our multilingual LLM. Marco-LLM is a pioneering multilingual LLM designed to not only perform exceptionally well in multilingual tasks, including low-resource languages, but also maintain strong performance in English and other major languages, closing the performance gap between high- and low-resource language capabilities. By bridging languages, this effort demonstrates our dedication to ensuring LLMs work accurately across various languages.

Hyperparameter Tuning Through Pessimistic Bilevel Optimization

Automated hyperparameter search in machine learning, especially for deep learning models, is typically formulated as a bilevel optimization problem, with hyperparameter values determined by the upper level and the model learning achieved by the lower-level problem. Most of the existing bilevel optimization solutions either assume the uniqueness of the optimal training model given hyperparameters or adopt an optimistic view when the non-uniqueness issue emerges. Potential model uncertainty may arise when training complex models with limited data, especially when the uniqueness assumption is violated. Thus, the suitability of the optimistic view underlying current bilevel hyperparameter optimization solutions is questionable. In this paper, we propose pessimistic bilevel hyperparameter optimization to assure appropriate outer-level hyperparameters to better generalize the inner-level learned models, by explicitly incorporating potential uncertainty of the inner-level solution set. To solve the resulting computationally challenging pessimistic bilevel optimization problem, we develop a novel relaxation-based approximation method. It derives pessimistic solutions with more robust prediction models. In our empirical studies of automated hyperparameter search for binary linear classifiers, pessimistic solutions have demonstrated better prediction performances than optimistic counterparts when we have limited training data or perturbed testing data, showing the necessity of considering pessimistic solutions besides existing optimistic ones.

Marco-o1: Towards Open Reasoning Models for Open-Ended Solutions

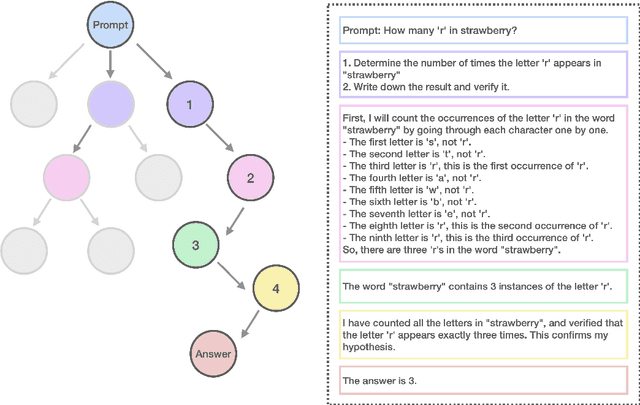
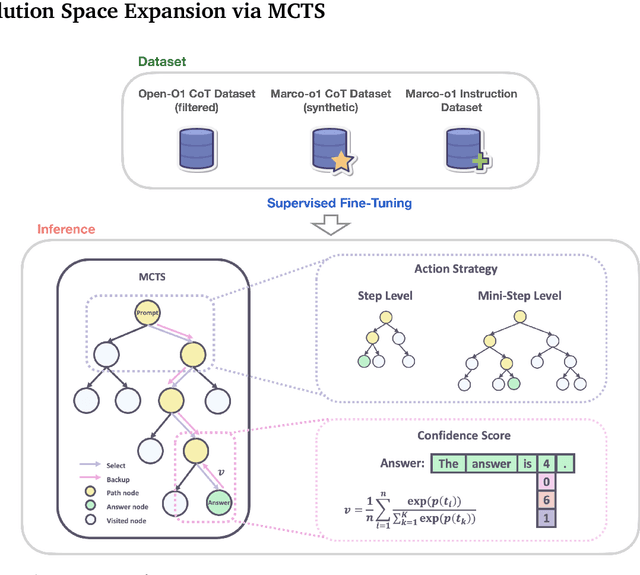
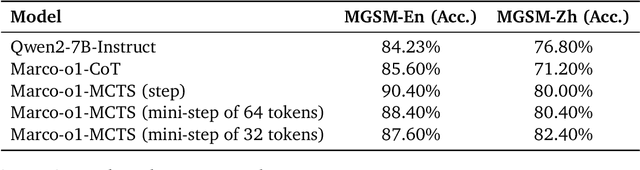
Currently OpenAI o1 has sparked a surge of interest in the study of large reasoning models (LRM). Building on this momentum, Marco-o1 not only focuses on disciplines with standard answers, such as mathematics, physics, and coding -- which are well-suited for reinforcement learning (RL) -- but also places greater emphasis on open-ended resolutions. We aim to address the question: "Can the o1 model effectively generalize to broader domains where clear standards are absent and rewards are challenging to quantify?" Marco-o1 is powered by Chain-of-Thought (CoT) fine-tuning, Monte Carlo Tree Search (MCTS), reflection mechanisms, and innovative reasoning strategies -- optimized for complex real-world problem-solving tasks.

HyperCLOVA X Technical Report

We introduce HyperCLOVA X, a family of large language models (LLMs) tailored to the Korean language and culture, along with competitive capabilities in English, math, and coding. HyperCLOVA X was trained on a balanced mix of Korean, English, and code data, followed by instruction-tuning with high-quality human-annotated datasets while abiding by strict safety guidelines reflecting our commitment to responsible AI. The model is evaluated across various benchmarks, including comprehensive reasoning, knowledge, commonsense, factuality, coding, math, chatting, instruction-following, and harmlessness, in both Korean and English. HyperCLOVA X exhibits strong reasoning capabilities in Korean backed by a deep understanding of the language and cultural nuances. Further analysis of the inherent bilingual nature and its extension to multilingualism highlights the model's cross-lingual proficiency and strong generalization ability to untargeted languages, including machine translation between several language pairs and cross-lingual inference tasks. We believe that HyperCLOVA X can provide helpful guidance for regions or countries in developing their sovereign LLMs.

Inverse Multiobjective Optimization Through Online Learning

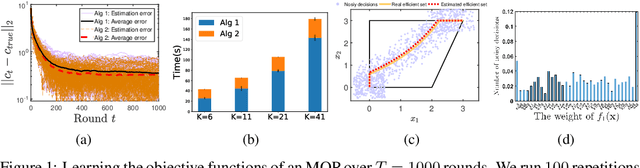
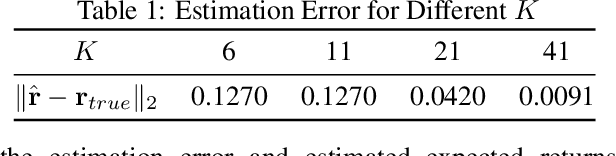
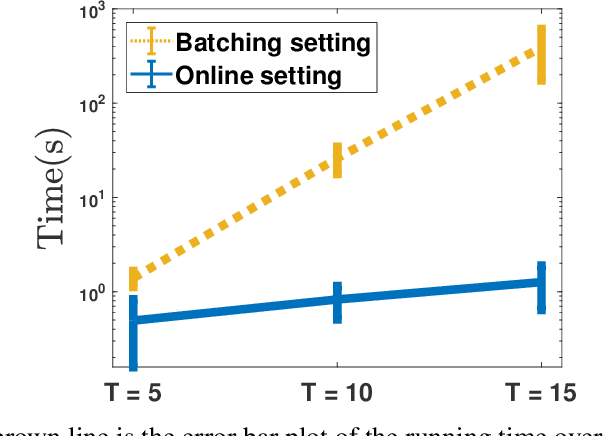
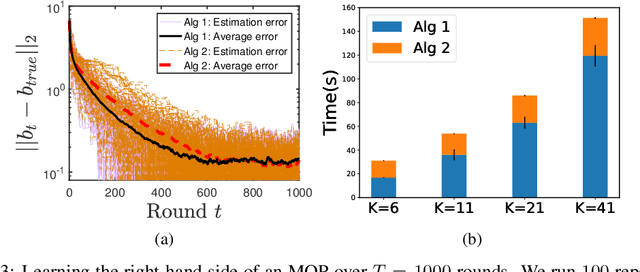
We study the problem of learning the objective functions or constraints of a multiobjective decision making model, based on a set of sequentially arrived decisions. In particular, these decisions might not be exact and possibly carry measurement noise or are generated with the bounded rationality of decision makers. In this paper, we propose a general online learning framework to deal with this learning problem using inverse multiobjective optimization. More precisely, we develop two online learning algorithms with implicit update rules which can handle noisy data. Numerical results show that both algorithms can learn the parameters with great accuracy and are robust to noise.

Wasserstein Distributionally Robust Inverse Multiobjective Optimization

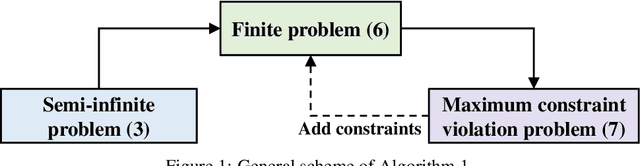
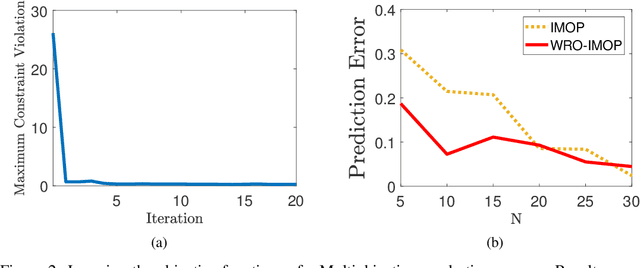
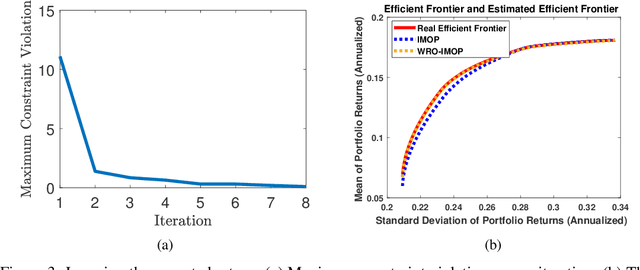
Inverse multiobjective optimization provides a general framework for the unsupervised learning task of inferring parameters of a multiobjective decision making problem (DMP), based on a set of observed decisions from the human expert. However, the performance of this framework relies critically on the availability of an accurate DMP, sufficient decisions of high quality, and a parameter space that contains enough information about the DMP. To hedge against the uncertainties in the hypothetical DMP, the data, and the parameter space, we investigate in this paper the distributionally robust approach for inverse multiobjective optimization. Specifically, we leverage the Wasserstein metric to construct a ball centered at the empirical distribution of these decisions. We then formulate a Wasserstein distributionally robust inverse multiobjective optimization problem (WRO-IMOP) that minimizes a worst-case expected loss function, where the worst case is taken over all distributions in the Wasserstein ball. We show that the excess risk of the WRO-IMOP estimator has a sub-linear convergence rate. Furthermore, we propose the semi-infinite reformulations of the WRO-IMOP and develop a cutting-plane algorithm that converges to an approximate solution in finite iterations. Finally, we demonstrate the effectiveness of our method on both a synthetic multiobjective quadratic program and a real world portfolio optimization problem.

Adversarial Attack on Hierarchical Graph Pooling Neural Networks

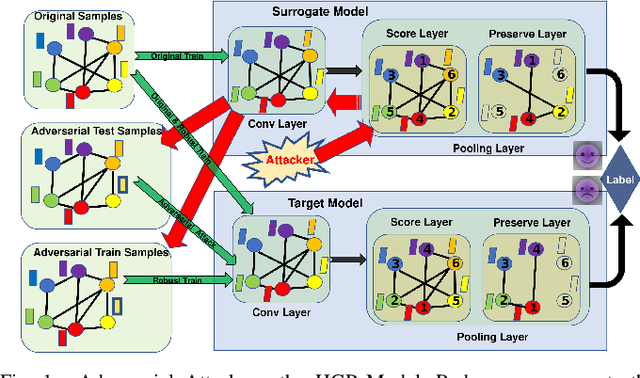
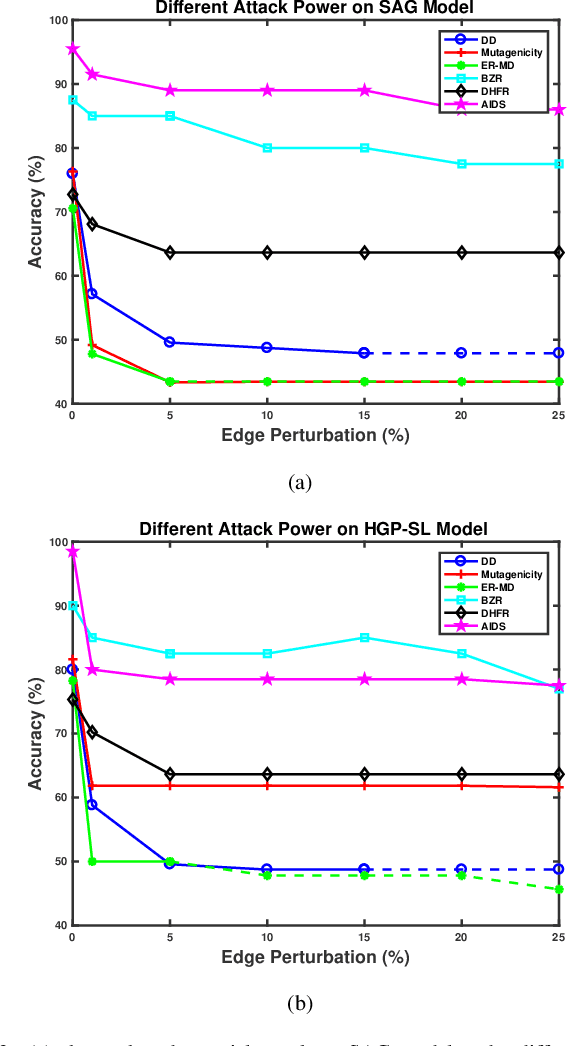
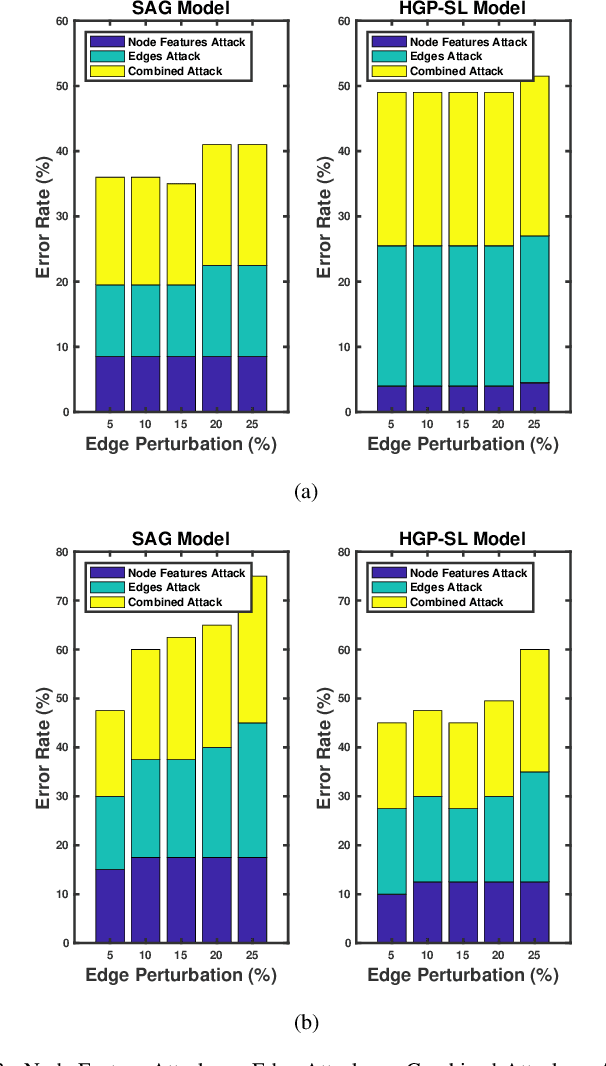
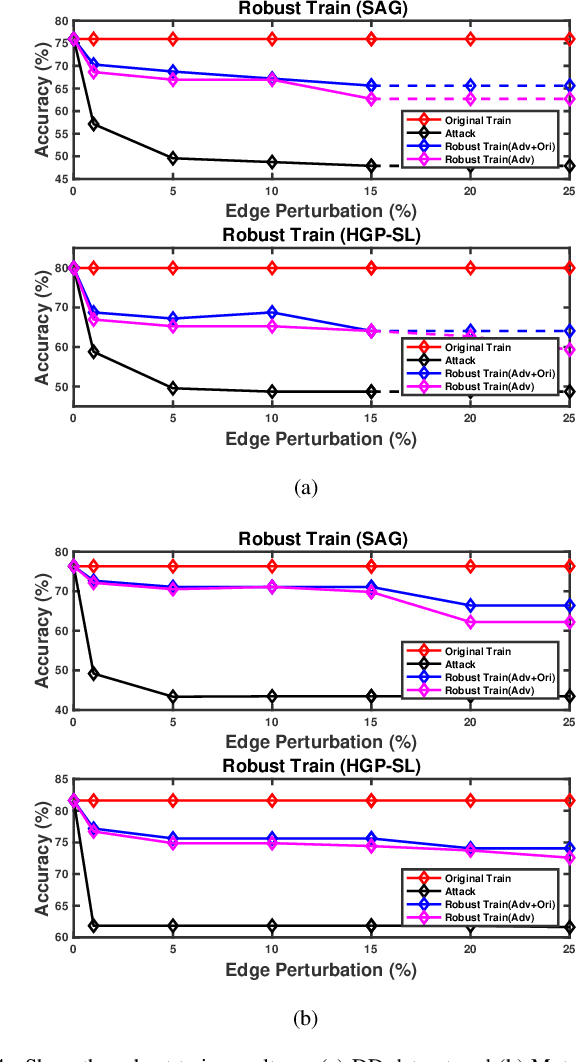
Recent years have witnessed the emergence and development of graph neural networks (GNNs), which have been shown as a powerful approach for graph representation learning in many tasks, such as node classification and graph classification. The research on the robustness of these models has also started to attract attentions in the machine learning field. However, most of the existing work in this area focus on the GNNs for node-level tasks, while little work has been done to study the robustness of the GNNs for the graph classification task. In this paper, we aim to explore the vulnerability of the Hierarchical Graph Pooling (HGP) Neural Networks, which are advanced GNNs that perform very well in the graph classification in terms of prediction accuracy. We propose an adversarial attack framework for this task. Specifically, we design a surrogate model that consists of convolutional and pooling operators to generate adversarial samples to fool the hierarchical GNN-based graph classification models. We set the preserved nodes by the pooling operator as our attack targets, and then we perturb the attack targets slightly to fool the pooling operator in hierarchical GNNs so that they will select the wrong nodes to preserve. We show the adversarial samples generated from multiple datasets by our surrogate model have enough transferability to attack current state-of-art graph classification models. Furthermore, we conduct the robust train on the target models and demonstrate that the retrained graph classification models are able to better defend against the attack from the adversarial samples. To the best of our knowledge, this is the first work on the adversarial attack against hierarchical GNN-based graph classification models.