Wasserstein Distributionally Robust Inverse Multiobjective Optimization
Paper and Code
Sep 30, 2020
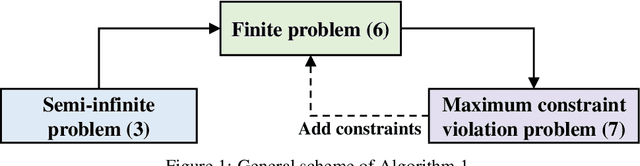
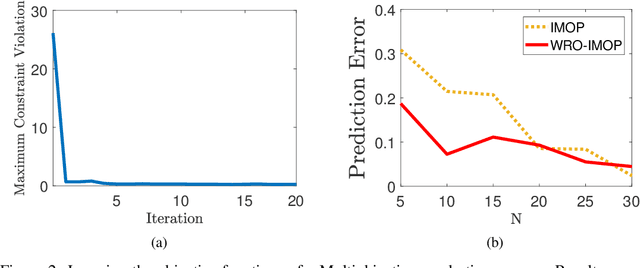
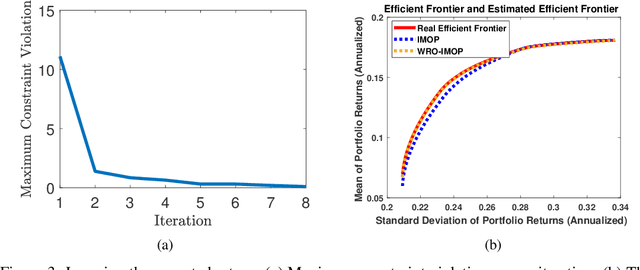
Inverse multiobjective optimization provides a general framework for the unsupervised learning task of inferring parameters of a multiobjective decision making problem (DMP), based on a set of observed decisions from the human expert. However, the performance of this framework relies critically on the availability of an accurate DMP, sufficient decisions of high quality, and a parameter space that contains enough information about the DMP. To hedge against the uncertainties in the hypothetical DMP, the data, and the parameter space, we investigate in this paper the distributionally robust approach for inverse multiobjective optimization. Specifically, we leverage the Wasserstein metric to construct a ball centered at the empirical distribution of these decisions. We then formulate a Wasserstein distributionally robust inverse multiobjective optimization problem (WRO-IMOP) that minimizes a worst-case expected loss function, where the worst case is taken over all distributions in the Wasserstein ball. We show that the excess risk of the WRO-IMOP estimator has a sub-linear convergence rate. Furthermore, we propose the semi-infinite reformulations of the WRO-IMOP and develop a cutting-plane algorithm that converges to an approximate solution in finite iterations. Finally, we demonstrate the effectiveness of our method on both a synthetic multiobjective quadratic program and a real world portfolio optimization problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge