Optimization Hyper-parameter Laws for Large Language Models

Large Language Models have driven significant AI advancements, yet their training is resource-intensive and highly sensitive to hyper-parameter selection. While scaling laws provide valuable guidance on model size and data requirements, they fall short in choosing dynamic hyper-parameters, such as learning-rate (LR) schedules, that evolve during training. To bridge this gap, we present Optimization Hyper-parameter Laws (Opt-Laws), a framework that effectively captures the relationship between hyper-parameters and training outcomes, enabling the pre-selection of potential optimal schedules. Grounded in stochastic differential equations, Opt-Laws introduce novel mathematical interpretability and offer a robust theoretical foundation for some popular LR schedules. Our extensive validation across diverse model sizes and data scales demonstrates Opt-Laws' ability to accurately predict training loss and identify optimal LR schedule candidates in pre-training, continual training, and fine-tuning scenarios. This approach significantly reduces computational costs while enhancing overall model performance.

LoCo: Low-Bit Communication Adaptor for Large-scale Model Training

To efficiently train large-scale models, low-bit gradient communication compresses full-precision gradients on local GPU nodes into low-precision ones for higher gradient synchronization efficiency among GPU nodes. However, it often degrades training quality due to compression information loss. To address this, we propose the Low-bit Communication Adaptor (LoCo), which compensates gradients on local GPU nodes before compression, ensuring efficient synchronization without compromising training quality. Specifically, LoCo designs a moving average of historical compensation errors to stably estimate concurrent compression error and then adopts it to compensate for the concurrent gradient compression, yielding a less lossless compression. This mechanism allows it to be compatible with general optimizers like Adam and sharding strategies like FSDP. Theoretical analysis shows that integrating LoCo into full-precision optimizers like Adam and SGD does not impair their convergence speed on nonconvex problems. Experimental results show that across large-scale model training frameworks like Megatron-LM and PyTorch's FSDP, LoCo significantly improves communication efficiency, e.g., improving Adam's training speed by 14% to 40% without performance degradation on large language models like LLAMAs and MoE.

On the Algorithmic Bias of Aligning Large Language Models with RLHF: Preference Collapse and Matching Regularization

Accurately aligning large language models (LLMs) with human preferences is crucial for informing fair, economically sound, and statistically efficient decision-making processes. However, we argue that reinforcement learning from human feedback (RLHF) -- the predominant approach for aligning LLMs with human preferences through a reward model -- suffers from an inherent algorithmic bias due to its Kullback--Leibler-based regularization in optimization. In extreme cases, this bias could lead to a phenomenon we term preference collapse, where minority preferences are virtually disregarded. To mitigate this algorithmic bias, we introduce preference matching (PM) RLHF, a novel approach that provably aligns LLMs with the preference distribution of the reward model under the Bradley--Terry--Luce/Plackett--Luce model. Central to our approach is a PM regularizer that takes the form of the negative logarithm of the LLM's policy probability distribution over responses, which helps the LLM balance response diversification and reward maximization. Notably, we obtain this regularizer by solving an ordinary differential equation that is necessary for the PM property. For practical implementation, we introduce a conditional variant of PM RLHF that is tailored to natural language generation. Finally, we empirically validate the effectiveness of conditional PM RLHF through experiments on the OPT-1.3B and Llama-2-7B models, demonstrating a 29% to 41% improvement in alignment with human preferences, as measured by a certain metric, compared to standard RLHF.

Task-Robust Pre-Training for Worst-Case Downstream Adaptation

Pre-training has achieved remarkable success when transferred to downstream tasks. In machine learning, we care about not only the good performance of a model but also its behavior under reasonable shifts of condition. The same philosophy holds when pre-training a foundation model. However, the foundation model may not uniformly behave well for a series of related downstream tasks. This happens, for example, when conducting mask recovery regression where the recovery ability or the training instances diverge like pattern features are extracted dominantly on pre-training, but semantic features are also required on a downstream task. This paper considers pre-training a model that guarantees a uniformly good performance over the downstream tasks. We call this goal as $\textit{downstream-task robustness}$. Our method first separates the upstream task into several representative ones and applies a simple minimax loss for pre-training. We then design an efficient algorithm to solve the minimax loss and prove its convergence in the convex setting. In the experiments, we show both on large-scale natural language processing and computer vision datasets our method increases the metrics on worse-case downstream tasks. Additionally, some theoretical explanations for why our loss is beneficial are provided. Specifically, we show fewer samples are inherently required for the most challenging downstream task in some cases.

Adan: Adaptive Nesterov Momentum Algorithm for Faster Optimizing Deep Models

Adaptive gradient algorithms borrow the moving average idea of heavy ball acceleration to estimate accurate first- and second-order moments of gradient for accelerating convergence. However, Nesterov acceleration which converges faster than heavy ball acceleration in theory and also in many empirical cases is much less investigated under the adaptive gradient setting. In this work, we propose the ADAptive Nesterov momentum algorithm, Adan for short, to speed up the training of deep neural networks effectively. Adan first reformulates the vanilla Nesterov acceleration to develop a new Nesterov momentum estimation (NME) method, which avoids the extra computation and memory overhead of computing gradient at the extrapolation point. Then Adan adopts NME to estimate the first- and second-order moments of the gradient in adaptive gradient algorithms for convergence acceleration. Besides, we prove that Adan finds an $\epsilon$-approximate first-order stationary point within $O(\epsilon^{-3.5})$ stochastic gradient complexity on the nonconvex stochastic problems (e.g., deep learning problems), matching the best-known lower bound. Extensive experimental results show that Adan surpasses the corresponding SoTA optimizers on both vision transformers (ViTs) and CNNs, and sets new SoTAs for many popular networks, e.g., ResNet, ConvNext, ViT, Swin, MAE, LSTM, Transformer-XL, and BERT. More surprisingly, Adan can use half of the training cost (epochs) of SoTA optimizers to achieve higher or comparable performance on ViT and ResNet, e.t.c., and also shows great tolerance to a large range of minibatch size, e.g., from 1k to 32k. We hope Adan can contribute to the development of deep learning by reducing training cost and relieving engineering burden of trying different optimizers on various architectures. Code is released at https://github.com/sail-sg/Adan.

Global Convergence of Over-parameterized Deep Equilibrium Models

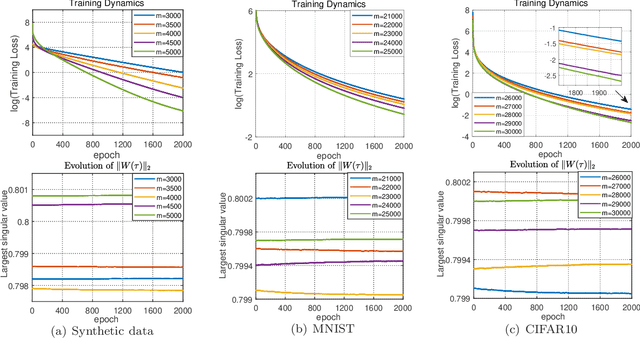
A deep equilibrium model (DEQ) is implicitly defined through an equilibrium point of an infinite-depth weight-tied model with an input-injection. Instead of infinite computations, it solves an equilibrium point directly with root-finding and computes gradients with implicit differentiation. The training dynamics of over-parameterized DEQs are investigated in this study. By supposing a condition on the initial equilibrium point, we show that the unique equilibrium point always exists during the training process, and the gradient descent is proved to converge to a globally optimal solution at a linear convergence rate for the quadratic loss function. In order to show that the required initial condition is satisfied via mild over-parameterization, we perform a fine-grained analysis on random DEQs. We propose a novel probabilistic framework to overcome the technical difficulty in the non-asymptotic analysis of infinite-depth weight-tied models.

High Quality Segmentation for Ultra High-resolution Images

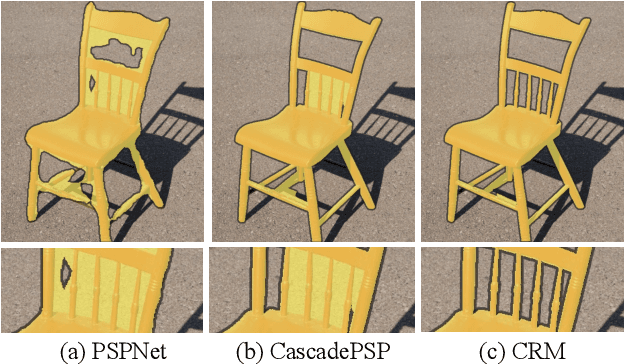
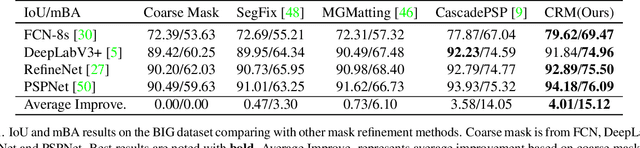
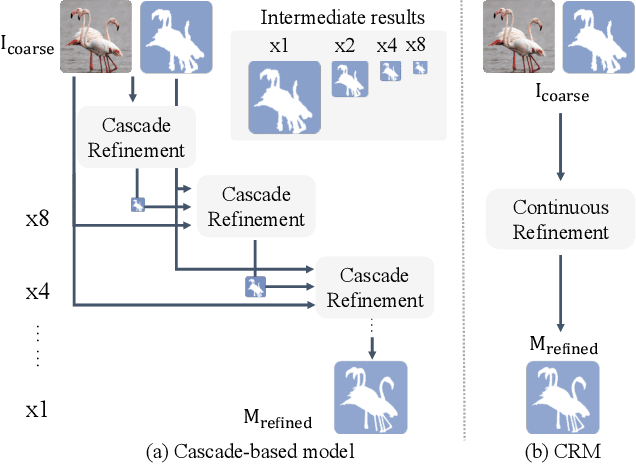
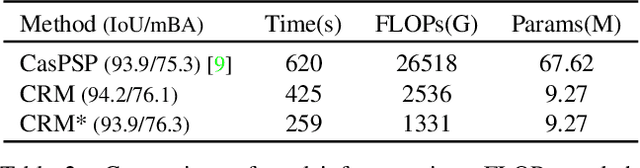
To segment 4K or 6K ultra high-resolution images needs extra computation consideration in image segmentation. Common strategies, such as down-sampling, patch cropping, and cascade model, cannot address well the balance issue between accuracy and computation cost. Motivated by the fact that humans distinguish among objects continuously from coarse to precise levels, we propose the Continuous Refinement Model~(CRM) for the ultra high-resolution segmentation refinement task. CRM continuously aligns the feature map with the refinement target and aggregates features to reconstruct these images' details. Besides, our CRM shows its significant generalization ability to fill the resolution gap between low-resolution training images and ultra high-resolution testing ones. We present quantitative performance evaluation and visualization to show that our proposed method is fast and effective on image segmentation refinement. Code will be released at https://github.com/dvlab-research/Entity.

Optimization Induced Equilibrium Networks

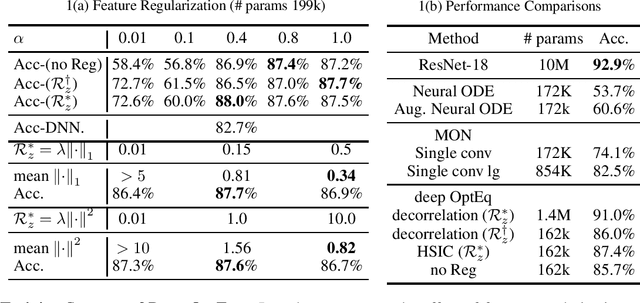
Implicit equilibrium models, i.e., deep neural networks (DNNs) defined by implicit equations, have been becoming more and more attractive recently. In this paper, we investigate an emerging question: can an implicit equilibrium model's equilibrium point be regarded as the solution of an optimization problem? To this end, we first decompose DNNs into a new class of unit layer that is the proximal operator of an implicit convex function while keeping its output unchanged. Then, the equilibrium model of the unit layer can be derived, named Optimization Induced Equilibrium Networks (OptEq), which can be easily extended to deep layers. The equilibrium point of OptEq can be theoretically connected to the solution of its corresponding convex optimization problem with explicit objectives. Based on this, we can flexibly introduce prior properties to the equilibrium points: 1) modifying the underlying convex problems explicitly so as to change the architectures of OptEq; and 2) merging the information into the fixed point iteration, which guarantees to choose the desired equilibrium point when the fixed point set is non-singleton. We show that deep OptEq outperforms previous implicit models even with fewer parameters. This work establishes the first step towards the optimization-guided design of deep models.

Maximum-and-Concatenation Networks

While successful in many fields, deep neural networks (DNNs) still suffer from some open problems such as bad local minima and unsatisfactory generalization performance. In this work, we propose a novel architecture called Maximum-and-Concatenation Networks (MCN) to try eliminating bad local minima and improving generalization ability as well. Remarkably, we prove that MCN has a very nice property; that is, \emph{every local minimum of an $(l+1)$-layer MCN can be better than, at least as good as, the global minima of the network consisting of its first $l$ layers}. In other words, by increasing the network depth, MCN can autonomously improve its local minima's goodness, what is more, \emph{it is easy to plug MCN into an existing deep model to make it also have this property}. Finally, under mild conditions, we show that MCN can approximate certain continuous functions arbitrarily well with \emph{high efficiency}; that is, the covering number of MCN is much smaller than most existing DNNs such as deep ReLU. Based on this, we further provide a tight generalization bound to guarantee the inference ability of MCN when dealing with testing samples.

Differentiable Linearized ADMM

Recently, a number of learning-based optimization methods that combine data-driven architectures with the classical optimization algorithms have been proposed and explored, showing superior empirical performance in solving various ill-posed inverse problems, but there is still a scarcity of rigorous analysis about the convergence behaviors of learning-based optimization. In particular, most existing analyses are specific to unconstrained problems but cannot apply to the more general cases where some variables of interest are subject to certain constraints. In this paper, we propose Differentiable Linearized ADMM (D-LADMM) for solving the problems with linear constraints. Specifically, D-LADMM is a K-layer LADMM inspired deep neural network, which is obtained by firstly introducing some learnable weights in the classical Linearized ADMM algorithm and then generalizing the proximal operator to some learnable activation function. Notably, we rigorously prove that there exist a set of learnable parameters for D-LADMM to generate globally converged solutions, and we show that those desired parameters can be attained by training D-LADMM in a proper way. To the best of our knowledge, we are the first to provide the convergence analysis for the learning-based optimization method on constrained problems.