Optimization Hyper-parameter Laws for Large Language Models

Large Language Models have driven significant AI advancements, yet their training is resource-intensive and highly sensitive to hyper-parameter selection. While scaling laws provide valuable guidance on model size and data requirements, they fall short in choosing dynamic hyper-parameters, such as learning-rate (LR) schedules, that evolve during training. To bridge this gap, we present Optimization Hyper-parameter Laws (Opt-Laws), a framework that effectively captures the relationship between hyper-parameters and training outcomes, enabling the pre-selection of potential optimal schedules. Grounded in stochastic differential equations, Opt-Laws introduce novel mathematical interpretability and offer a robust theoretical foundation for some popular LR schedules. Our extensive validation across diverse model sizes and data scales demonstrates Opt-Laws' ability to accurately predict training loss and identify optimal LR schedule candidates in pre-training, continual training, and fine-tuning scenarios. This approach significantly reduces computational costs while enhancing overall model performance.

Skywork-Math: Data Scaling Laws for Mathematical Reasoning in Large Language Models -- The Story Goes On

In this paper, we investigate the underlying factors that potentially enhance the mathematical reasoning capabilities of large language models (LLMs). We argue that the data scaling law for math reasoning capabilities in modern LLMs is far from being saturated, highlighting how the model's quality improves with increases in data quantity. To support this claim, we introduce the Skywork-Math model series, supervised fine-tuned (SFT) on common 7B LLMs using our proposed 2.5M-instance Skywork-MathQA dataset. Skywork-Math 7B has achieved impressive accuracies of 51.2% on the competition-level MATH benchmark and 83.9% on the GSM8K benchmark using only SFT data, outperforming an early version of GPT-4 on MATH. The superior performance of Skywork-Math models contributes to our novel two-stage data synthesis and model SFT pipelines, which include three different augmentation methods and a diverse seed problem set, ensuring both the quantity and quality of Skywork-MathQA dataset across varying difficulty levels. Most importantly, we provide several practical takeaways to enhance math reasoning abilities in LLMs for both research and industry applications.

Skywork-MoE: A Deep Dive into Training Techniques for Mixture-of-Experts Language Models

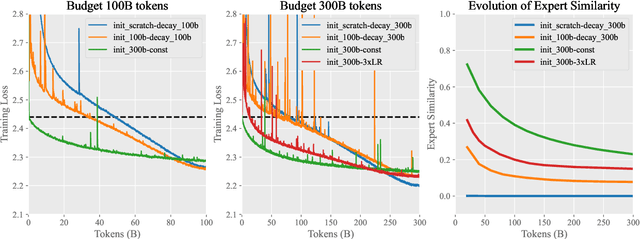
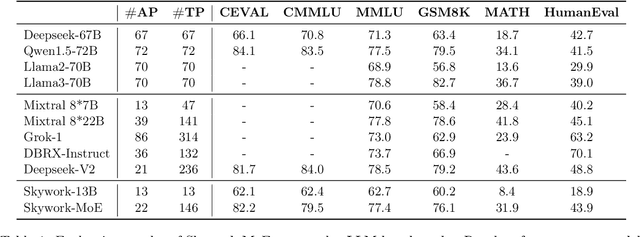
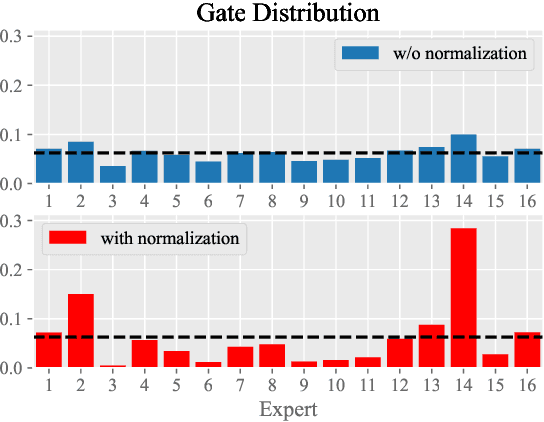
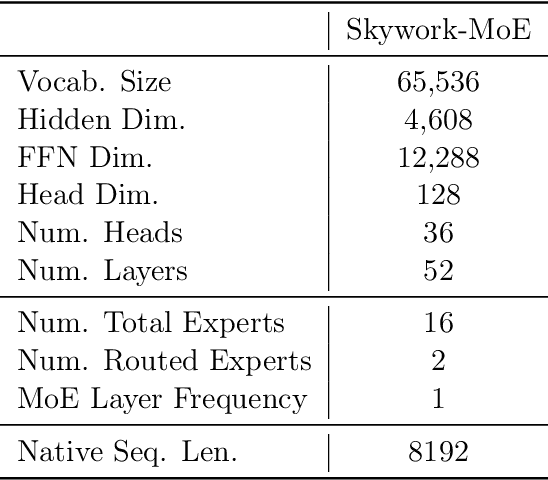
In this technical report, we introduce the training methodologies implemented in the development of Skywork-MoE, a high-performance mixture-of-experts (MoE) large language model (LLM) with 146 billion parameters and 16 experts. It is initialized from the pre-existing dense checkpoints of our Skywork-13B model. We explore the comparative effectiveness of upcycling versus training from scratch initializations. Our findings suggest that the choice between these two approaches should consider both the performance of the existing dense checkpoints and the MoE training budget. We highlight two innovative techniques: gating logit normalization, which improves expert diversification, and adaptive auxiliary loss coefficients, allowing for layer-specific adjustment of auxiliary loss coefficients. Our experimental results validate the effectiveness of these methods. Leveraging these techniques and insights, we trained our upcycled Skywork-MoE on a condensed subset of our SkyPile corpus. The evaluation results demonstrate that our model delivers strong performance across a wide range of benchmarks.

LongSkywork: A Training Recipe for Efficiently Extending Context Length in Large Language Models

We introduce LongSkywork, a long-context Large Language Model (LLM) capable of processing up to 200,000 tokens. We provide a training recipe for efficiently extending context length of LLMs. We identify that the critical element in enhancing long-context processing capability is to incorporate a long-context SFT stage following the standard SFT stage. A mere 200 iterations can convert the standard SFT model into a long-context model. To reduce the effort in collecting and annotating data for long-context language modeling, we develop two novel methods for creating synthetic data. These methods are applied during the continual pretraining phase as well as the Supervised Fine-Tuning (SFT) phase, greatly enhancing the training efficiency of our long-context LLMs. Our findings suggest that synthetic long-context SFT data can surpass the performance of data curated by humans to some extent. LongSkywork achieves outstanding performance on a variety of long-context benchmarks. In the Needle test, a benchmark for long-context information retrieval, our models achieved perfect accuracy across multiple context spans. Moreover, in realistic application scenarios, LongSkywork-13B demonstrates performance on par with Claude2.1, the leading long-context model, underscoring the effectiveness of our proposed methods.

Skywork: A More Open Bilingual Foundation Model

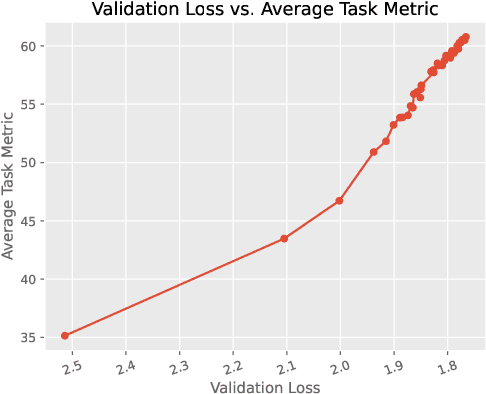
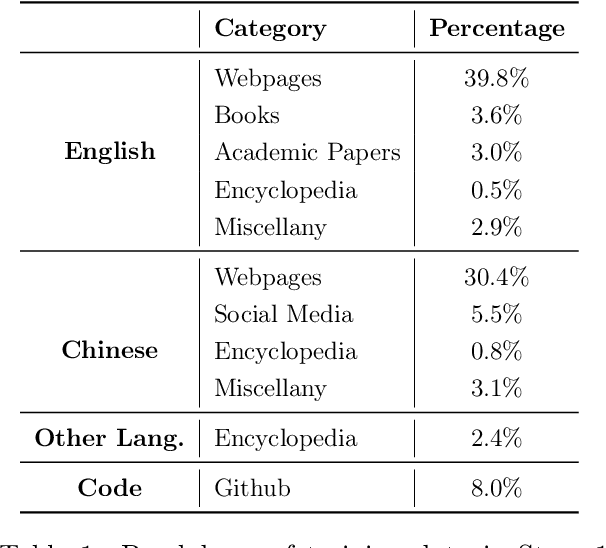
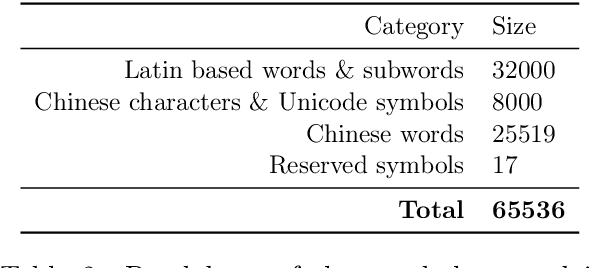
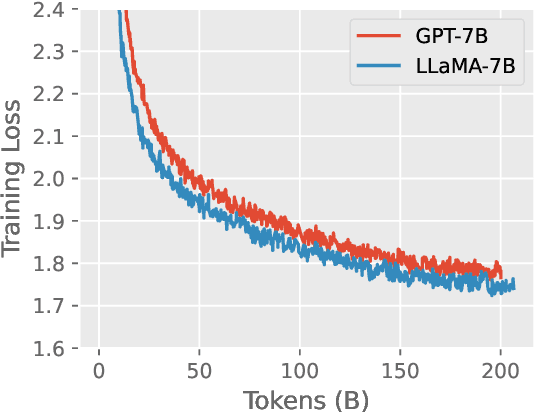
In this technical report, we present Skywork-13B, a family of large language models (LLMs) trained on a corpus of over 3.2 trillion tokens drawn from both English and Chinese texts. This bilingual foundation model is the most extensively trained and openly published LLMs of comparable size to date. We introduce a two-stage training methodology using a segmented corpus, targeting general purpose training and then domain-specific enhancement training, respectively. We show that our model not only excels on popular benchmarks, but also achieves \emph{state of the art} performance in Chinese language modeling on diverse domains. Furthermore, we propose a novel leakage detection method, demonstrating that test data contamination is a pressing issue warranting further investigation by the LLM community. To spur future research, we release Skywork-13B along with checkpoints obtained during intermediate stages of the training process. We are also releasing part of our SkyPile corpus, a collection of over 150 billion tokens of web text, which is the largest high quality open Chinese pre-training corpus to date. We hope Skywork-13B and our open corpus will serve as a valuable open-source resource to democratize access to high-quality LLMs.

SkyMath: Technical Report

Large language models (LLMs) have shown great potential to solve varieties of natural language processing (NLP) tasks, including mathematical reasoning. In this work, we present SkyMath, a large language model for mathematics with 13 billion parameters. By applying self-compare fine-tuning, we have enhanced mathematical reasoning abilities of Skywork-13B-Base remarkably. On GSM8K, SkyMath outperforms all known open-source models of similar size and has established a new SOTA performance.

CMATH: Can Your Language Model Pass Chinese Elementary School Math Test?

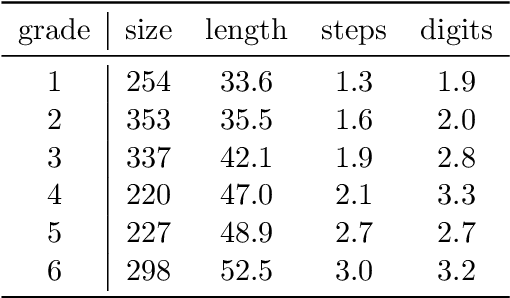
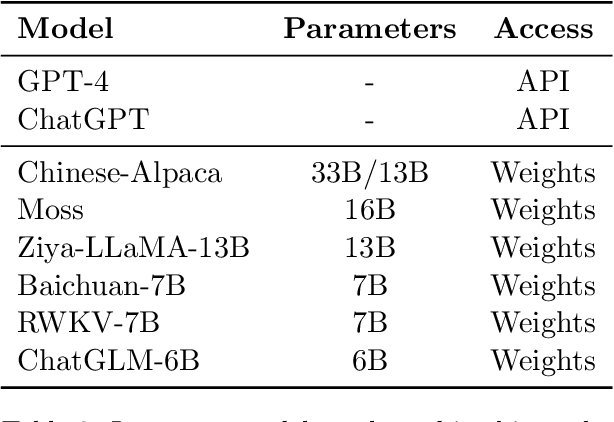
We present the Chinese Elementary School Math Word Problems (CMATH) dataset, comprising 1.7k elementary school-level math word problems with detailed annotations, source from actual Chinese workbooks and exams. This dataset aims to provide a benchmark tool for assessing the following question: to what grade level of elementary school math do the abilities of popular large language models (LLMs) correspond? We evaluate a variety of popular LLMs, including both commercial and open-source options, and discover that only GPT-4 achieves success (accuracy $\geq$ 60\%) across all six elementary school grades, while other models falter at different grade levels. Furthermore, we assess the robustness of several top-performing LLMs by augmenting the original problems in the CMATH dataset with distracting information. Our findings reveal that GPT-4 is able to maintains robustness, while other model fail. We anticipate that our study will expose limitations in LLMs' arithmetic and reasoning capabilities, and promote their ongoing development and advancement.

A Flexible Multi-Task Model for BERT Serving

In this demonstration, we present an efficient BERT-based multi-task (MT) framework that is particularly suitable for iterative and incremental development of the tasks. The proposed framework is based on the idea of partial fine-tuning, i.e. only fine-tune some top layers of BERT while keep the other layers frozen. For each task, we train independently a single-task (ST) model using partial fine-tuning. Then we compress the task-specific layers in each ST model using knowledge distillation. Those compressed ST models are finally merged into one MT model so that the frozen layers of the former are shared across the tasks. We exemplify our approach on eight GLUE tasks, demonstrating that it is able to achieve both strong performance and efficiency. We have implemented our method in the utterance understanding system of XiaoAI, a commercial AI assistant developed by Xiaomi. We estimate that our model reduces the overall serving cost by 86%.

Masked Conditional Random Fields for Sequence Labeling

Conditional Random Field (CRF) based neural models are among the most performant methods for solving sequence labeling problems. Despite its great success, CRF has the shortcoming of occasionally generating illegal sequences of tags, e.g. sequences containing an "I-" tag immediately after an "O" tag, which is forbidden by the underlying BIO tagging scheme. In this work, we propose Masked Conditional Random Field (MCRF), an easy to implement variant of CRF that impose restrictions on candidate paths during both training and decoding phases. We show that the proposed method thoroughly resolves this issue and brings consistent improvement over existing CRF-based models with near zero additional cost.

A convergence and asymptotic analysis of the generalized symmetric FastICA algorithm

This contribution deals with the generalized symmetric FastICA algorithm in the domain of Independent Component Analysis (ICA). The generalized symmetric version of FastICA has been shown to have the potential to achieve the Cram\'er-Rao Bound (CRB) by allowing the usage of different nonlinearity functions in its parallel implementations of one-unit FastICA. In spite of this appealing property, a rigorous study of the asymptotic error of the generalized symmetric FastICA algorithm is still missing in the community. In fact, all the existing results exhibit certain limitations, such as ignoring the impact of data standardization on the asymptotic statistics or being based on a heuristic approach. In this work, we aim at filling this blank. The first result of this contribution is the characterization of the limits of the generalized symmetric FastICA. It is shown that the algorithm optimizes a function that is a sum of the contrast functions used by traditional one-unit FastICA with a correction of the sign. Based on this characterization, we derive a closed-form analytic expression of the asymptotic covariance matrix of the generalized symmetric FastICA estimator using the method of estimating equation and M-estimator.