Optimization Induced Equilibrium Networks
Paper and Code
Jun 07, 2021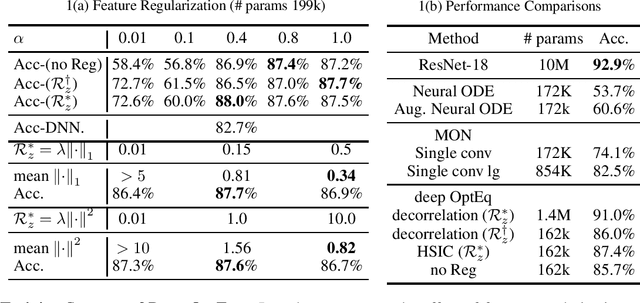


Implicit equilibrium models, i.e., deep neural networks (DNNs) defined by implicit equations, have been becoming more and more attractive recently. In this paper, we investigate an emerging question: can an implicit equilibrium model's equilibrium point be regarded as the solution of an optimization problem? To this end, we first decompose DNNs into a new class of unit layer that is the proximal operator of an implicit convex function while keeping its output unchanged. Then, the equilibrium model of the unit layer can be derived, named Optimization Induced Equilibrium Networks (OptEq), which can be easily extended to deep layers. The equilibrium point of OptEq can be theoretically connected to the solution of its corresponding convex optimization problem with explicit objectives. Based on this, we can flexibly introduce prior properties to the equilibrium points: 1) modifying the underlying convex problems explicitly so as to change the architectures of OptEq; and 2) merging the information into the fixed point iteration, which guarantees to choose the desired equilibrium point when the fixed point set is non-singleton. We show that deep OptEq outperforms previous implicit models even with fewer parameters. This work establishes the first step towards the optimization-guided design of deep models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge