Langming Liu
ECKGBench: Benchmarking Large Language Models in E-commerce Leveraging Knowledge Graph
Mar 20, 2025Abstract:Large language models (LLMs) have demonstrated their capabilities across various NLP tasks. Their potential in e-commerce is also substantial, evidenced by practical implementations such as platform search, personalized recommendations, and customer service. One primary concern associated with LLMs is their factuality (e.g., hallucination), which is urgent in e-commerce due to its significant impact on user experience and revenue. Despite some methods proposed to evaluate LLMs' factuality, issues such as lack of reliability, high consumption, and lack of domain expertise leave a gap between effective assessment in e-commerce. To bridge the evaluation gap, we propose ECKGBench, a dataset specifically designed to evaluate the capacities of LLMs in e-commerce knowledge. Specifically, we adopt a standardized workflow to automatically generate questions based on a large-scale knowledge graph, guaranteeing sufficient reliability. We employ the simple question-answering paradigm, substantially improving the evaluation efficiency by the least input and output tokens. Furthermore, we inject abundant e-commerce expertise in each evaluation stage, including human annotation, prompt design, negative sampling, and verification. Besides, we explore the LLMs' knowledge boundaries in e-commerce from a novel perspective. Through comprehensive evaluations of several advanced LLMs on ECKGBench, we provide meticulous analysis and insights into leveraging LLMs for e-commerce.
ChineseEcomQA: A Scalable E-commerce Concept Evaluation Benchmark for Large Language Models
Feb 27, 2025
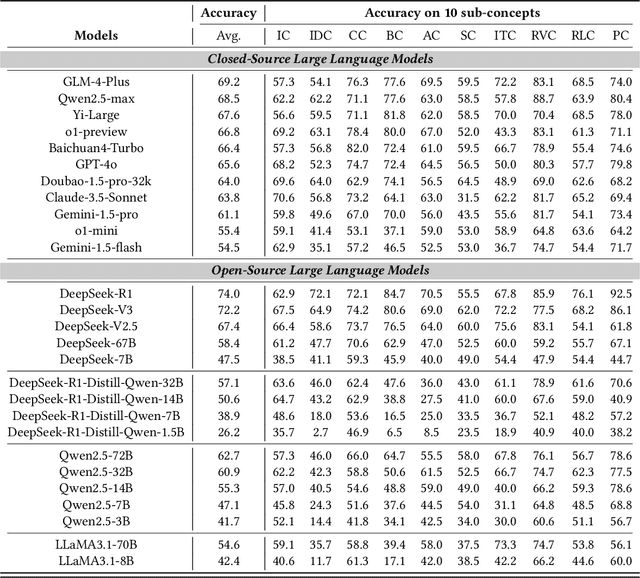
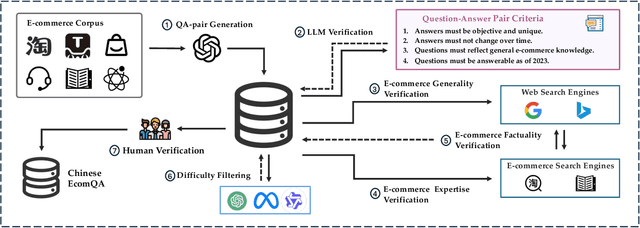

Abstract:With the increasing use of Large Language Models (LLMs) in fields such as e-commerce, domain-specific concept evaluation benchmarks are crucial for assessing their domain capabilities. Existing LLMs may generate factually incorrect information within the complex e-commerce applications. Therefore, it is necessary to build an e-commerce concept benchmark. Existing benchmarks encounter two primary challenges: (1) handle the heterogeneous and diverse nature of tasks, (2) distinguish between generality and specificity within the e-commerce field. To address these problems, we propose \textbf{ChineseEcomQA}, a scalable question-answering benchmark focused on fundamental e-commerce concepts. ChineseEcomQA is built on three core characteristics: \textbf{Focus on Fundamental Concept}, \textbf{E-commerce Generality} and \textbf{E-commerce Expertise}. Fundamental concepts are designed to be applicable across a diverse array of e-commerce tasks, thus addressing the challenge of heterogeneity and diversity. Additionally, by carefully balancing generality and specificity, ChineseEcomQA effectively differentiates between broad e-commerce concepts, allowing for precise validation of domain capabilities. We achieve this through a scalable benchmark construction process that combines LLM validation, Retrieval-Augmented Generation (RAG) validation, and rigorous manual annotation. Based on ChineseEcomQA, we conduct extensive evaluations on mainstream LLMs and provide some valuable insights. We hope that ChineseEcomQA could guide future domain-specific evaluations, and facilitate broader LLM adoption in e-commerce applications.
UQABench: Evaluating User Embedding for Prompting LLMs in Personalized Question Answering
Feb 26, 2025Abstract:Large language models (LLMs) achieve remarkable success in natural language processing (NLP). In practical scenarios like recommendations, as users increasingly seek personalized experiences, it becomes crucial to incorporate user interaction history into the context of LLMs to enhance personalization. However, from a practical utility perspective, user interactions' extensive length and noise present challenges when used directly as text prompts. A promising solution is to compress and distill interactions into compact embeddings, serving as soft prompts to assist LLMs in generating personalized responses. Although this approach brings efficiency, a critical concern emerges: Can user embeddings adequately capture valuable information and prompt LLMs? To address this concern, we propose \name, a benchmark designed to evaluate the effectiveness of user embeddings in prompting LLMs for personalization. We establish a fair and standardized evaluation process, encompassing pre-training, fine-tuning, and evaluation stages. To thoroughly evaluate user embeddings, we design three dimensions of tasks: sequence understanding, action prediction, and interest perception. These evaluation tasks cover the industry's demands in traditional recommendation tasks, such as improving prediction accuracy, and its aspirations for LLM-based methods, such as accurately understanding user interests and enhancing the user experience. We conduct extensive experiments on various state-of-the-art methods for modeling user embeddings. Additionally, we reveal the scaling laws of leveraging user embeddings to prompt LLMs. The benchmark is available online.
Unlocking Scaling Law in Industrial Recommendation Systems with a Three-step Paradigm based Large User Model
Feb 12, 2025Abstract:Recent advancements in autoregressive Large Language Models (LLMs) have achieved significant milestones, largely attributed to their scalability, often referred to as the "scaling law". Inspired by these achievements, there has been a growing interest in adapting LLMs for Recommendation Systems (RecSys) by reformulating RecSys tasks into generative problems. However, these End-to-End Generative Recommendation (E2E-GR) methods tend to prioritize idealized goals, often at the expense of the practical advantages offered by traditional Deep Learning based Recommendation Models (DLRMs) in terms of in features, architecture, and practices. This disparity between idealized goals and practical needs introduces several challenges and limitations, locking the scaling law in industrial RecSys. In this paper, we introduce a large user model (LUM) that addresses these limitations through a three-step paradigm, designed to meet the stringent requirements of industrial settings while unlocking the potential for scalable recommendations. Our extensive experimental evaluations demonstrate that LUM outperforms both state-of-the-art DLRMs and E2E-GR approaches. Notably, LUM exhibits excellent scalability, with performance improvements observed as the model scales up to 7 billion parameters. Additionally, we have successfully deployed LUM in an industrial application, where it achieved significant gains in an A/B test, further validating its effectiveness and practicality.
LinRec: Linear Attention Mechanism for Long-term Sequential Recommender Systems
Nov 03, 2024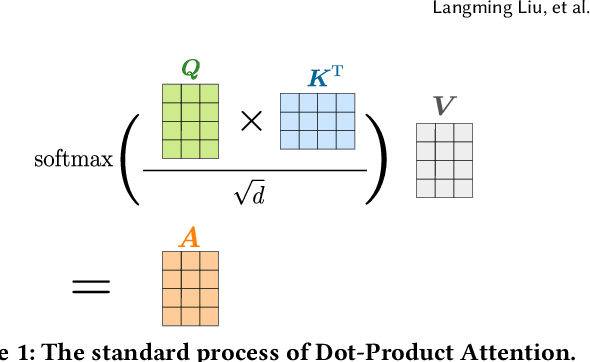
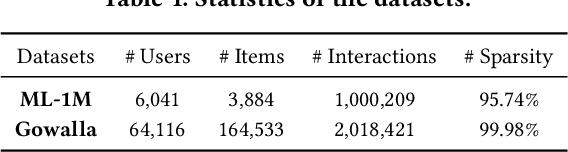
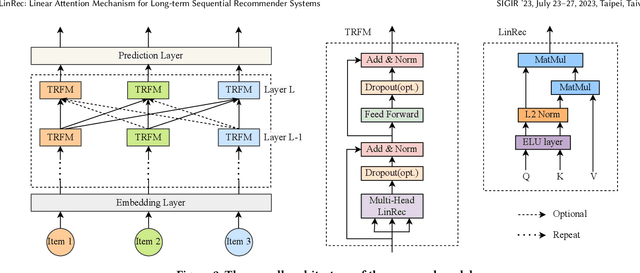
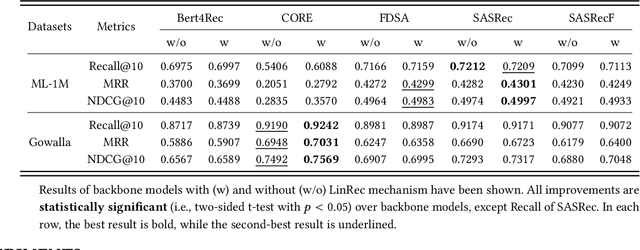
Abstract:Transformer models have achieved remarkable success in sequential recommender systems (SRSs). However, computing the attention matrix in traditional dot-product attention mechanisms results in a quadratic complexity with sequence lengths, leading to high computational costs for long-term sequential recommendation. Motivated by the above observation, we propose a novel L2-Normalized Linear Attention for the Transformer-based Sequential Recommender Systems (LinRec), which theoretically improves efficiency while preserving the learning capabilities of the traditional dot-product attention. Specifically, by thoroughly examining the equivalence conditions of efficient attention mechanisms, we show that LinRec possesses linear complexity while preserving the property of attention mechanisms. In addition, we reveal its latent efficiency properties by interpreting the proposed LinRec mechanism through a statistical lens. Extensive experiments are conducted based on two public benchmark datasets, demonstrating that the combination of LinRec and Transformer models achieves comparable or even superior performance than state-of-the-art Transformer-based SRS models while significantly improving time and memory efficiency.
Efficient and Robust Regularized Federated Recommendation
Nov 03, 2024



Abstract:Recommender systems play a pivotal role across practical scenarios, showcasing remarkable capabilities in user preference modeling. However, the centralized learning paradigm predominantly used raises serious privacy concerns. The federated recommender system (FedRS) addresses this by updating models on clients, while a central server orchestrates training without accessing private data. Existing FedRS approaches, however, face unresolved challenges, including non-convex optimization, vulnerability, potential privacy leakage risk, and communication inefficiency. This paper addresses these challenges by reformulating the federated recommendation problem as a convex optimization issue, ensuring convergence to the global optimum. Based on this, we devise a novel method, RFRec, to tackle this optimization problem efficiently. In addition, we propose RFRecF, a highly efficient version that incorporates non-uniform stochastic gradient descent to improve communication efficiency. In user preference modeling, both methods learn local and global models, collaboratively learning users' common and personalized interests under the federated learning setting. Moreover, both methods significantly enhance communication efficiency, robustness, and privacy protection, with theoretical support. Comprehensive evaluations on four benchmark datasets demonstrate RFRec and RFRecF's superior performance compared to diverse baselines.
Analysis of regularized federated learning
Nov 03, 2024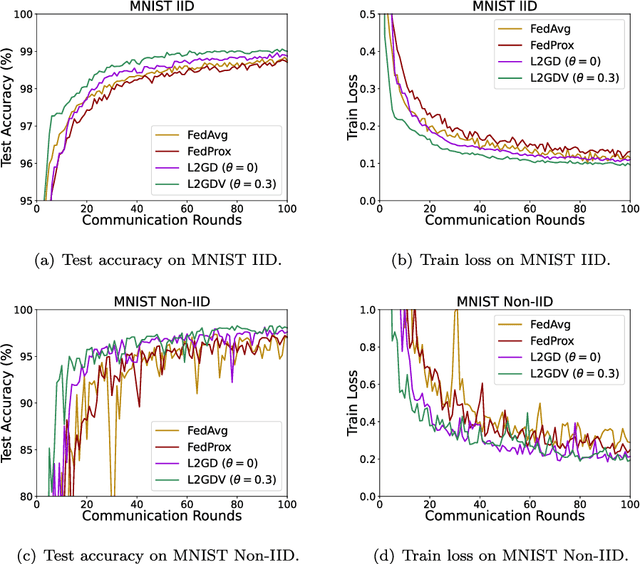
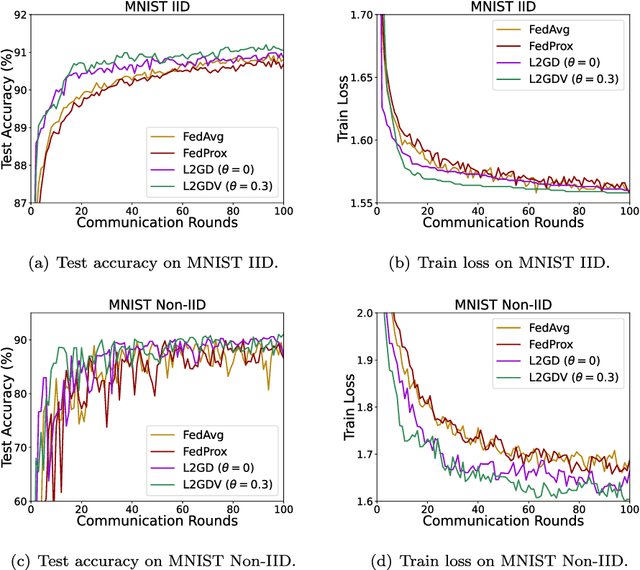
Abstract:Federated learning is an efficient machine learning tool for dealing with heterogeneous big data and privacy protection. Federated learning methods with regularization can control the level of communications between the central and local machines. Stochastic gradient descent is often used for implementing such methods on heterogeneous big data, to reduce the communication costs. In this paper, we consider such an algorithm called Loopless Local Gradient Descent which has advantages in reducing the expected communications by controlling a probability level. We improve the method by allowing flexible step sizes and carry out novel analysis for the convergence of the algorithm in a non-convex setting in addition to the standard strongly convex setting. In the non-convex setting, we derive rates of convergence when the smooth objective function satisfies a Polyak-{\L}ojasiewicz condition. When the objective function is strongly convex, a sufficient and necessary condition for the convergence in expectation is presented.
Cumulative Distribution Function based General Temporal Point Processes
Feb 01, 2024Abstract:Temporal Point Processes (TPPs) hold a pivotal role in modeling event sequences across diverse domains, including social networking and e-commerce, and have significantly contributed to the advancement of recommendation systems and information retrieval strategies. Through the analysis of events such as user interactions and transactions, TPPs offer valuable insights into behavioral patterns, facilitating the prediction of future trends. However, accurately forecasting future events remains a formidable challenge due to the intricate nature of these patterns. The integration of Neural Networks with TPPs has ushered in the development of advanced deep TPP models. While these models excel at processing complex and nonlinear temporal data, they encounter limitations in modeling intensity functions, grapple with computational complexities in integral computations, and struggle to capture long-range temporal dependencies effectively. In this study, we introduce the CuFun model, representing a novel approach to TPPs that revolves around the Cumulative Distribution Function (CDF). CuFun stands out by uniquely employing a monotonic neural network for CDF representation, utilizing past events as a scaling factor. This innovation significantly bolsters the model's adaptability and precision across a wide range of data scenarios. Our approach addresses several critical issues inherent in traditional TPP modeling: it simplifies log-likelihood calculations, extends applicability beyond predefined density function forms, and adeptly captures long-range temporal patterns. Our contributions encompass the introduction of a pioneering CDF-based TPP model, the development of a methodology for incorporating past event information into future event prediction, and empirical validation of CuFun's effectiveness through extensive experimentation on synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge