Analysis of regularized federated learning
Paper and Code
Nov 03, 2024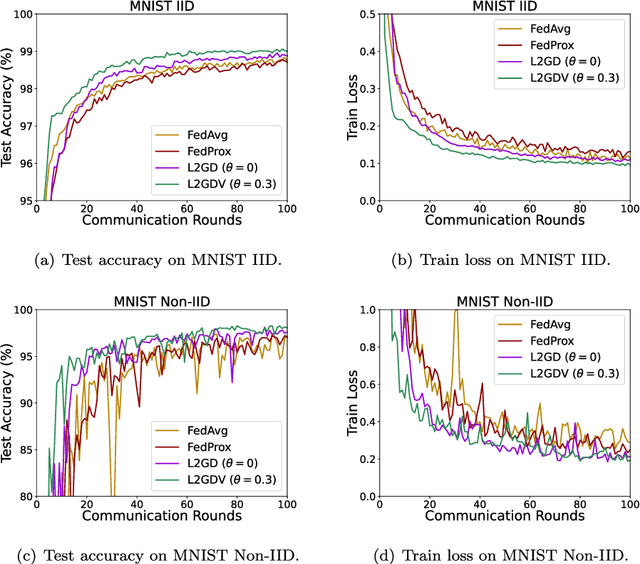
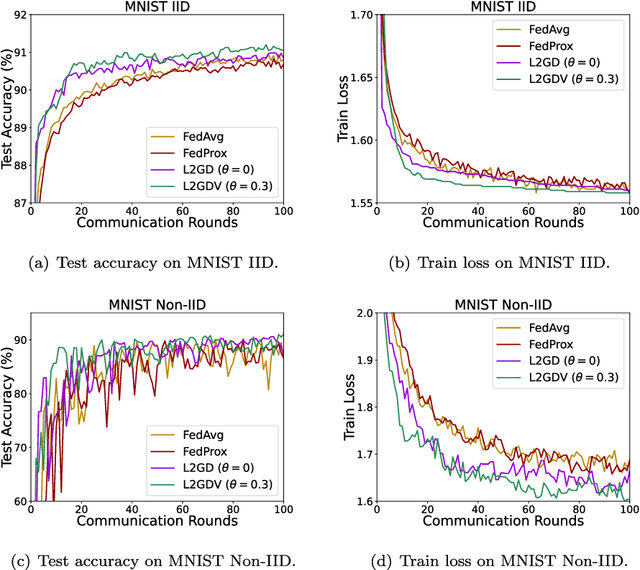
Federated learning is an efficient machine learning tool for dealing with heterogeneous big data and privacy protection. Federated learning methods with regularization can control the level of communications between the central and local machines. Stochastic gradient descent is often used for implementing such methods on heterogeneous big data, to reduce the communication costs. In this paper, we consider such an algorithm called Loopless Local Gradient Descent which has advantages in reducing the expected communications by controlling a probability level. We improve the method by allowing flexible step sizes and carry out novel analysis for the convergence of the algorithm in a non-convex setting in addition to the standard strongly convex setting. In the non-convex setting, we derive rates of convergence when the smooth objective function satisfies a Polyak-{\L}ojasiewicz condition. When the objective function is strongly convex, a sufficient and necessary condition for the convergence in expectation is presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge