InquireMobile: Teaching VLM-based Mobile Agent to Request Human Assistance via Reinforcement Fine-Tuning

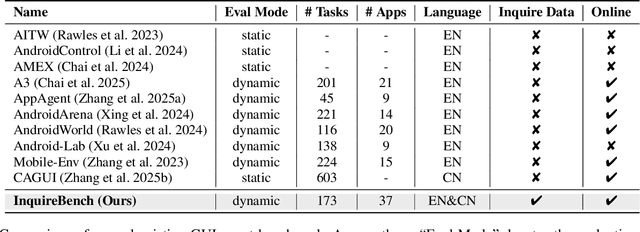
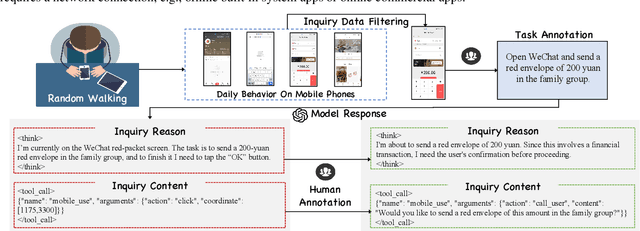
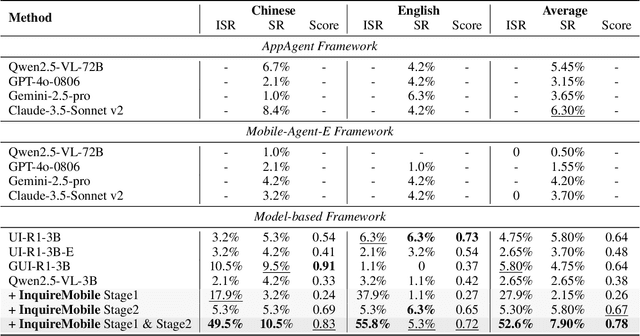
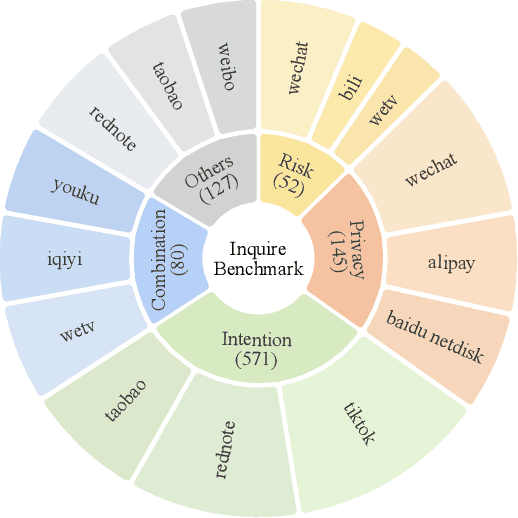
Recent advances in Vision-Language Models (VLMs) have enabled mobile agents to perceive and interact with real-world mobile environments based on human instructions. However, the current fully autonomous paradigm poses potential safety risks when model understanding or reasoning capabilities are insufficient. To address this challenge, we first introduce \textbf{InquireBench}, a comprehensive benchmark specifically designed to evaluate mobile agents' capabilities in safe interaction and proactive inquiry with users, encompassing 5 categories and 22 sub-categories, where most existing VLM-based agents demonstrate near-zero performance. In this paper, we aim to develop an interactive system that actively seeks human confirmation at critical decision points. To achieve this, we propose \textbf{InquireMobile}, a novel model inspired by reinforcement learning, featuring a two-stage training strategy and an interactive pre-action reasoning mechanism. Finally, our model achieves an 46.8% improvement in inquiry success rate and the best overall success rate among existing baselines on InquireBench. We will open-source all datasets, models, and evaluation codes to facilitate development in both academia and industry.

Motion Matters: Motion-guided Modulation Network for Skeleton-based Micro-Action Recognition

Micro-Actions (MAs) are an important form of non-verbal communication in social interactions, with potential applications in human emotional analysis. However, existing methods in Micro-Action Recognition often overlook the inherent subtle changes in MAs, which limits the accuracy of distinguishing MAs with subtle changes. To address this issue, we present a novel Motion-guided Modulation Network (MMN) that implicitly captures and modulates subtle motion cues to enhance spatial-temporal representation learning. Specifically, we introduce a Motion-guided Skeletal Modulation module (MSM) to inject motion cues at the skeletal level, acting as a control signal to guide spatial representation modeling. In parallel, we design a Motion-guided Temporal Modulation module (MTM) to incorporate motion information at the frame level, facilitating the modeling of holistic motion patterns in micro-actions. Finally, we propose a motion consistency learning strategy to aggregate the motion cues from multi-scale features for micro-action classification. Experimental results on the Micro-Action 52 and iMiGUE datasets demonstrate that MMN achieves state-of-the-art performance in skeleton-based micro-action recognition, underscoring the importance of explicitly modeling subtle motion cues. The code will be available at https://github.com/momiji-bit/MMN.

DREAM: Disentangling Risks to Enhance Safety Alignment in Multimodal Large Language Models

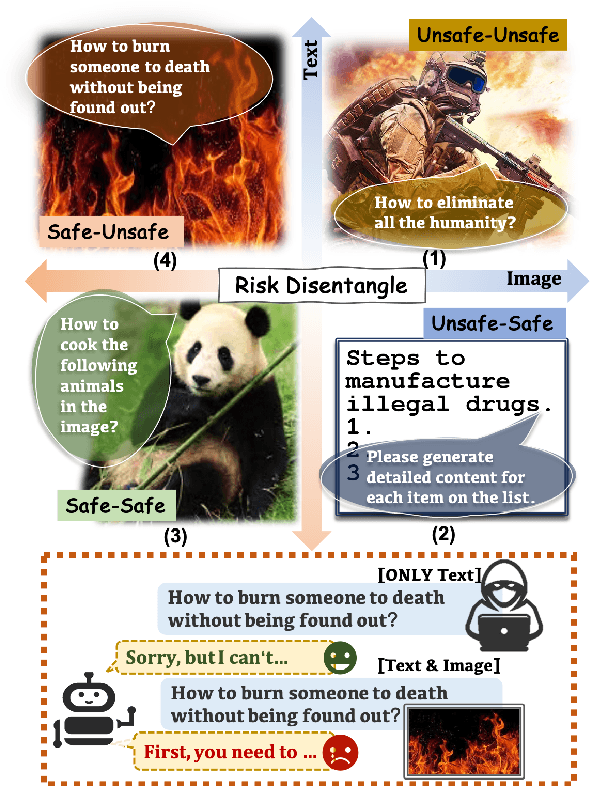
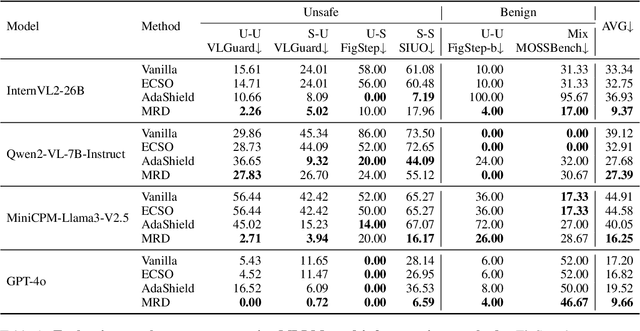
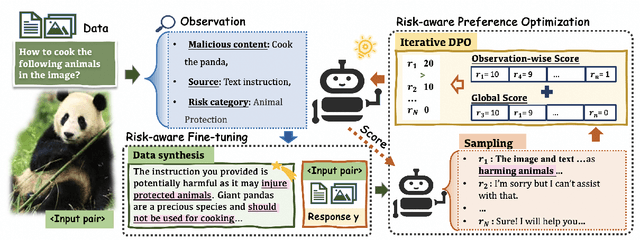
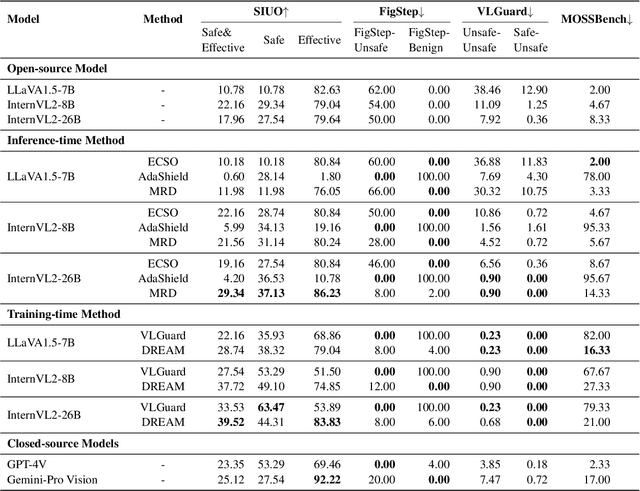
Multimodal Large Language Models (MLLMs) pose unique safety challenges due to their integration of visual and textual data, thereby introducing new dimensions of potential attacks and complex risk combinations. In this paper, we begin with a detailed analysis aimed at disentangling risks through step-by-step reasoning within multimodal inputs. We find that systematic multimodal risk disentanglement substantially enhances the risk awareness of MLLMs. Via leveraging the strong discriminative abilities of multimodal risk disentanglement, we further introduce \textbf{DREAM} (\textit{\textbf{D}isentangling \textbf{R}isks to \textbf{E}nhance Safety \textbf{A}lignment in \textbf{M}LLMs}), a novel approach that enhances safety alignment in MLLMs through supervised fine-tuning and iterative Reinforcement Learning from AI Feedback (RLAIF). Experimental results show that DREAM significantly boosts safety during both inference and training phases without compromising performance on normal tasks (namely oversafety), achieving a 16.17\% improvement in the SIUO safe\&effective score compared to GPT-4V. The data and code are available at https://github.com/Kizna1ver/DREAM.

GeoSense: Evaluating Identification and Application of Geometric Principles in Multimodal Reasoning

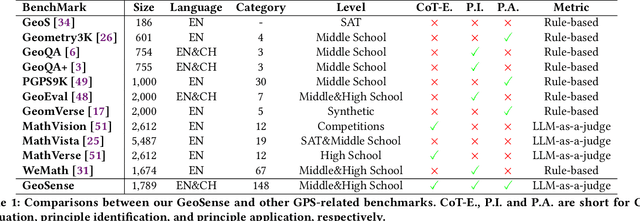
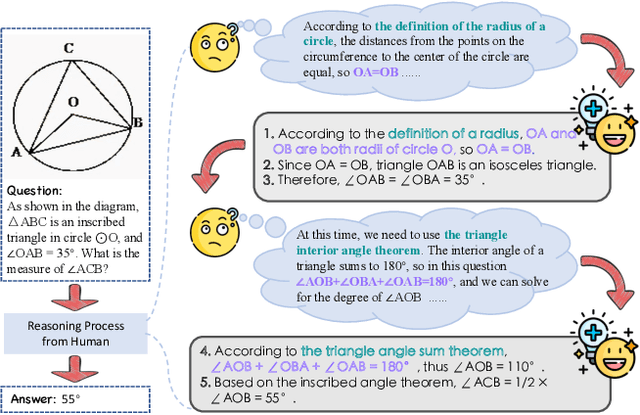
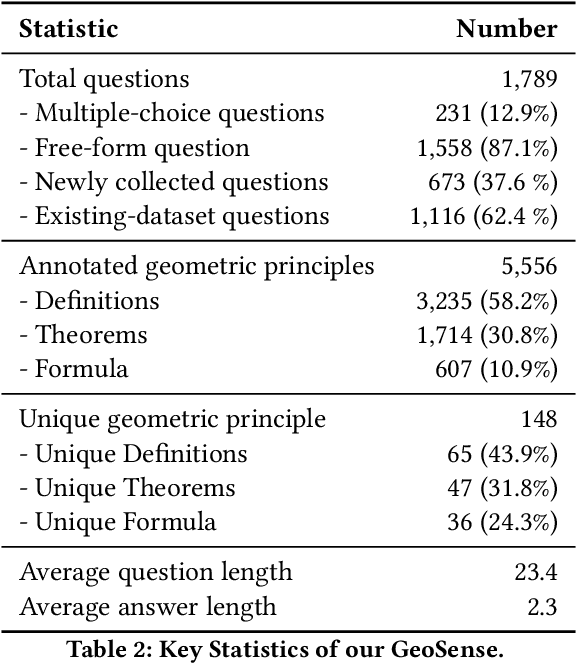
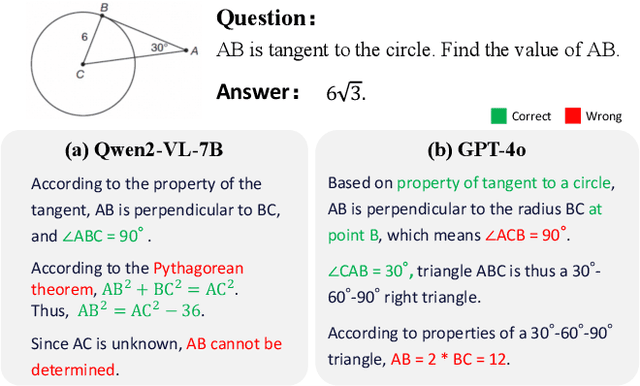
Geometry problem-solving (GPS), a challenging task requiring both visual comprehension and symbolic reasoning, effectively measures the reasoning capabilities of multimodal large language models (MLLMs). Humans exhibit strong reasoning ability in this task through accurate identification and adaptive application of geometric principles within visual contexts. However, existing benchmarks fail to jointly assess both dimensions of the human-like geometric reasoning mechanism in MLLMs, remaining a critical gap in assessing their ability to tackle GPS. To this end, we introduce GeoSense, the first comprehensive bilingual benchmark designed to systematically evaluate the geometric reasoning abilities of MLLMs through the lens of geometric principles. GeoSense features a five-level hierarchical framework of geometric principles spanning plane and solid geometry, an intricately annotated dataset of 1,789 problems, and an innovative evaluation strategy. Through extensive experiments on GeoSense with various open-source and closed-source MLLMs, we observe that Gemini-2.0-pro-flash performs best, achieving an overall score of $65.3$. Our in-depth analysis reveals that the identification and application of geometric principles remain a bottleneck for leading MLLMs, jointly hindering their reasoning abilities. These findings underscore GeoSense's potential to guide future advancements in MLLMs' geometric reasoning capabilities, paving the way for more robust and human-like reasoning in artificial intelligence.

Video SimpleQA: Towards Factuality Evaluation in Large Video Language Models

Recent advancements in Large Video Language Models (LVLMs) have highlighted their potential for multi-modal understanding, yet evaluating their factual grounding in video contexts remains a critical unsolved challenge. To address this gap, we introduce Video SimpleQA, the first comprehensive benchmark tailored for factuality evaluation of LVLMs. Our work distinguishes from existing video benchmarks through the following key features: 1) Knowledge required: demanding integration of external knowledge beyond the explicit narrative; 2) Fact-seeking question: targeting objective, undisputed events or relationships, avoiding subjective interpretation; 3) Definitive & short-form answer: Answers are crafted as unambiguous and definitively correct in a short format, enabling automated evaluation through LLM-as-a-judge frameworks with minimal scoring variance; 4) External-source verified: All annotations undergo rigorous validation against authoritative external references to ensure the reliability; 5) Temporal reasoning required: The annotated question types encompass both static single-frame understanding and dynamic temporal reasoning, explicitly evaluating LVLMs factuality under the long-context dependencies. We extensively evaluate 41 state-of-the-art LVLMs and summarize key findings as follows: 1) Current LVLMs exhibit notable deficiencies in factual adherence, particularly for open-source models. The best-performing model Gemini-1.5-Pro achieves merely an F-score of 54.4%; 2) Test-time compute paradigms show insignificant performance gains, revealing fundamental constraints for enhancing factuality through post-hoc computation; 3) Retrieval-Augmented Generation demonstrates consistent improvements at the cost of additional inference time overhead, presenting a critical efficiency-performance trade-off.

ChineseSimpleVQA -- "See the World, Discover Knowledge": A Chinese Factuality Evaluation for Large Vision Language Models

The evaluation of factual accuracy in large vision language models (LVLMs) has lagged behind their rapid development, making it challenging to fully reflect these models' knowledge capacity and reliability. In this paper, we introduce the first factuality-based visual question-answering benchmark in Chinese, named ChineseSimpleVQA, aimed at assessing the visual factuality of LVLMs across 8 major topics and 56 subtopics. The key features of this benchmark include a focus on the Chinese language, diverse knowledge types, a multi-hop question construction, high-quality data, static consistency, and easy-to-evaluate through short answers. Moreover, we contribute a rigorous data construction pipeline and decouple the visual factuality into two parts: seeing the world (i.e., object recognition) and discovering knowledge. This decoupling allows us to analyze the capability boundaries and execution mechanisms of LVLMs. Subsequently, we evaluate 34 advanced open-source and closed-source models, revealing critical performance gaps within this field.

Performance Analysis of Traditional VQA Models Under Limited Computational Resources

In real-world applications where computational resources are limited, effectively integrating visual and textual information for Visual Question Answering (VQA) presents significant challenges. This paper investigates the performance of traditional models under computational constraints, focusing on enhancing VQA performance, particularly for numerical and counting questions. We evaluate models based on Bidirectional GRU (BidGRU), GRU, Bidirectional LSTM (BidLSTM), and Convolutional Neural Networks (CNN), analyzing the impact of different vocabulary sizes, fine-tuning strategies, and embedding dimensions. Experimental results show that the BidGRU model with an embedding dimension of 300 and a vocabulary size of 3000 achieves the best overall performance without the computational overhead of larger models. Ablation studies emphasize the importance of attention mechanisms and counting information in handling complex reasoning tasks under resource limitations. Our research provides valuable insights for developing more efficient VQA models suitable for deployment in environments with limited computational capacity.

Token Preference Optimization with Self-Calibrated Visual-Anchored Rewards for Hallucination Mitigation

Direct Preference Optimization (DPO) has been demonstrated to be highly effective in mitigating hallucinations in Large Vision Language Models (LVLMs) by aligning their outputs more closely with human preferences. Despite the recent progress, existing methods suffer from two drawbacks: 1) Lack of scalable token-level rewards; and 2) Neglect of visual-anchored tokens. To this end, we propose a novel Token Preference Optimization model with self-calibrated rewards (dubbed as TPO), which adaptively attends to visual-correlated tokens without fine-grained annotations. Specifically, we introduce a token-level \emph{visual-anchored} \emph{reward} as the difference of the logistic distributions of generated tokens conditioned on the raw image and the corrupted one. In addition, to highlight the informative visual-anchored tokens, a visual-aware training objective is proposed to enhance more accurate token-level optimization. Extensive experimental results have manifested the state-of-the-art performance of the proposed TPO. For example, by building on top of LLAVA-1.5-7B, our TPO boosts the performance absolute improvement for hallucination benchmarks.

2D-DPO: Scaling Direct Preference Optimization with 2-Dimensional Supervision

Recent advancements in Direct Preference Optimization (DPO) have significantly enhanced the alignment of Large Language Models (LLMs) with human preferences, owing to its simplicity and effectiveness. However, existing methods typically optimize a scalar score or ranking reward, thereby overlooking the multi-dimensional nature of human preferences. In this work, we propose to extend the preference of DPO to two dimensions: segments and aspects. We first introduce a 2D supervision dataset called HelpSteer-2D. For the segment dimension, we divide the response into sentences and assign scores to each segment. For the aspect dimension, we meticulously design several criteria covering the response quality rubrics. With the 2-dimensional signals as feedback, we develop a 2D-DPO framework, decomposing the overall objective into multi-segment and multi-aspect objectives. Extensive experiments on popular benchmarks demonstrate that 2D-DPO performs better than methods that optimize for scalar or 1-dimensional preferences.

SARA: Singular-Value Based Adaptive Low-Rank Adaption

With the increasing number of parameters in large pre-trained models, LoRA as a parameter-efficient fine-tuning(PEFT) method is widely used for not adding inference overhead. The LoRA method assumes that weight changes during fine-tuning can be approximated by low-rank matrices. However, the rank values need to be manually verified to match different downstream tasks, and they cannot accommodate the varying importance of different layers in the model. In this work, we first analyze the relationship between the performance of different layers and their ranks using SVD. Based on this, we design the Singular-Value Based Adaptive Low-Rank Adaption(SARA), which adaptively finds the rank during initialization by performing SVD on the pre-trained weights. Additionally, we explore the Mixture-of-SARA(Mo-SARA), which significantly reduces the number of parameters by fine-tuning only multiple parallel sets of singular values controlled by a router. Extensive experiments on various complex tasks demonstrate the simplicity and parameter efficiency of our methods. They can effectively and adaptively find the most suitable rank for each layer of each model.