The Fourth Monocular Depth Estimation Challenge

This paper presents the results of the fourth edition of the Monocular Depth Estimation Challenge (MDEC), which focuses on zero-shot generalization to the SYNS-Patches benchmark, a dataset featuring challenging environments in both natural and indoor settings. In this edition, we revised the evaluation protocol to use least-squares alignment with two degrees of freedom to support disparity and affine-invariant predictions. We also revised the baselines and included popular off-the-shelf methods: Depth Anything v2 and Marigold. The challenge received a total of 24 submissions that outperformed the baselines on the test set; 10 of these included a report describing their approach, with most leading methods relying on affine-invariant predictions. The challenge winners improved the 3D F-Score over the previous edition's best result, raising it from 22.58% to 23.05%.

Unbiased Evaluation of Large Language Models from a Causal Perspective

Benchmark contamination has become a significant concern in the LLM evaluation community. Previous Agents-as-an-Evaluator address this issue by involving agents in the generation of questions. Despite their success, the biases in Agents-as-an-Evaluator methods remain largely unexplored. In this paper, we present a theoretical formulation of evaluation bias, providing valuable insights into designing unbiased evaluation protocols. Furthermore, we identify two type of bias in Agents-as-an-Evaluator through carefully designed probing tasks on a minimal Agents-as-an-Evaluator setup. To address these issues, we propose the Unbiased Evaluator, an evaluation protocol that delivers a more comprehensive, unbiased, and interpretable assessment of LLMs.Extensive experiments reveal significant room for improvement in current LLMs. Additionally, we demonstrate that the Unbiased Evaluator not only offers strong evidence of benchmark contamination but also provides interpretable evaluation results.

Joint Multitarget Detection and Tracking with mmWave Radar

Accurate targets detection and tracking with mmWave radar is a key sensing capability that will enable more intelligent systems, create smart, efficient, automated system. This paper proposes an end-to-end detection-estimation-track framework named MNOMP-SPA-KF consisting of the target detection and estimation module, the data association (DA) module and the target tracking module. In the target estimation and detection module, a low complexity, super-resolution and constant false alarm rate (CFAR) based two dimensional multisnapshot Newtonalized orthogonal matching pursuit (2D-MNOMP) is designed to extract the multitarget's radial distances and velocities, followed by the conventional (Bartlett) beamformer to extract the multitarget's azimuths. In the DA module, a sum product algorithm (SPA) is adopted to obtain the association probabilities of the existed targets and measurements by incorporating the radial velocity information. The Kalman filter (KF) is implemented to perform target tracking in the target tracking module by exploiting the asymptotic distribution of the estimators. To improve the detection probability of the weak targets, extrapolation is also coupled into the MNOMP-SPA-KF. Numerical and real data experiments demonstrate the effectiveness of the MNOMP-SPA-KF algorithm, compared to other benchmark algorithms.

Gaze Label Alignment: Alleviating Domain Shift for Gaze Estimation

Gaze estimation methods encounter significant performance deterioration when being evaluated across different domains, because of the domain gap between the testing and training data. Existing methods try to solve this issue by reducing the deviation of data distribution, however, they ignore the existence of label deviation in the data due to the acquisition mechanism of the gaze label and the individual physiological differences. In this paper, we first point out that the influence brought by the label deviation cannot be ignored, and propose a gaze label alignment algorithm (GLA) to eliminate the label distribution deviation. Specifically, we first train the feature extractor on all domains to get domain invariant features, and then select an anchor domain to train the gaze regressor. We predict the gaze label on remaining domains and use a mapping function to align the labels. Finally, these aligned labels can be used to train gaze estimation models. Therefore, our method can be combined with any existing method. Experimental results show that our GLA method can effectively alleviate the label distribution shift, and SOTA gaze estimation methods can be further improved obviously.

DM-SBL: Channel Estimation under Structured Interference

Channel estimation is a fundamental task in communication systems and is critical for effective demodulation. While most works deal with a simple scenario where the measurements are corrupted by the additive white Gaussian noise (AWGN), this work addresses the more challenging scenario where both AWGN and structured interference coexist. Such conditions arise, for example, when a sonar/radar transmitter and a communication receiver operate simultaneously within the same bandwidth. To ensure accurate channel estimation in these scenarios, the sparsity of the channel in the delay domain and the complicate structure of the interference are jointly exploited. Firstly, the score of the structured interference is learned via a neural network based on the diffusion model (DM), while the channel prior is modeled as a Gaussian distribution, with its variance controlling channel sparsity, similar to the setup of the sparse Bayesian learning (SBL). Then, two efficient posterior sampling methods are proposed to jointly estimate the sparse channel and the interference. Nuisance parameters, such as the variance of the prior are estimated via the expectation maximization (EM) algorithm. The proposed method is termed as DM based SBL (DM-SBL). Numerical simulations demonstrate that DM-SBL significantly outperforms conventional approaches that deal with the AWGN scenario, particularly under low signal-to-interference ratio (SIR) conditions. Beyond channel estimation, DM-SBL also shows promise for addressing other linear inverse problems involving structured interference.

LG-Gaze: Learning Geometry-aware Continuous Prompts for Language-Guided Gaze Estimation

The ability of gaze estimation models to generalize is often significantly hindered by various factors unrelated to gaze, especially when the training dataset is limited. Current strategies aim to address this challenge through different domain generalization techniques, yet they have had limited success due to the risk of overfitting when solely relying on value labels for regression. Recent progress in pre-trained vision-language models has motivated us to capitalize on the abundant semantic information available. We propose a novel approach in this paper, reframing the gaze estimation task as a vision-language alignment issue. Our proposed framework, named Language-Guided Gaze Estimation (LG-Gaze), learns continuous and geometry-sensitive features for gaze estimation benefit from the rich prior knowledges of vision-language models. Specifically, LG-Gaze aligns gaze features with continuous linguistic features through our proposed multimodal contrastive regression loss, which customizes adaptive weights for different negative samples. Furthermore, to better adapt to the labels for gaze estimation task, we propose a geometry-aware interpolation method to obtain more precise gaze embeddings. Through extensive experiments, we validate the efficacy of our framework in four different cross-domain evaluation tasks.

A Modulo Sampling Hardware Prototype and Reconstruction Algorithm Evaluation

Analog-to-digital converters (ADCs) play a vital important role in any devices via manipulating analog signals in a digital manner. Given that the amplitude of the signal exceeds the dynamic range of the ADCs, clipping occurs and the quality of the digitized signal degrades significantly. In this paper, we design a joint modulo sampling hardware and processing prototype which improves the ADCs' dynamic range by folding the signal before sampling. Both the detailed design of the hardware and the recovery results of various state-of-the-art processing algorithms including our proposed unlimited sampling line spectral estimation (USLSE) algorithm are presented. Additionally, key issues that arise during implementation are also addressed. It is demonstrated that the USLSE algorithm successfully recovers the original signal with a frequency of 2.5 kHz and an amplitude 10 times the ADC's dynamic range, and the linear prediction (LP) algorithm successfully recovers the original signal with a frequency of 3.5 kHz and an amplitude 10 times the ADC's dynamic range.

MOSE: Boosting Vision-based Roadside 3D Object Detection with Scene Cues

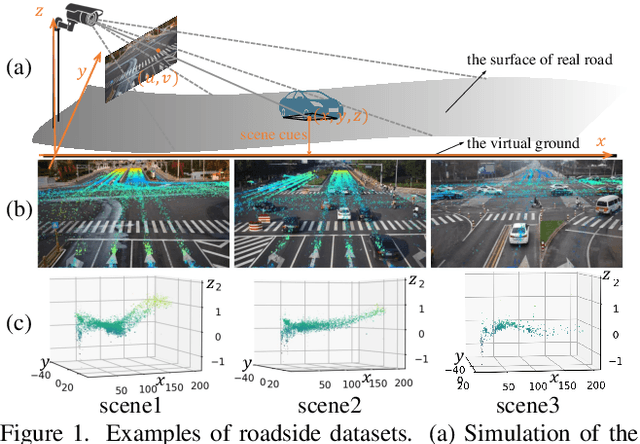
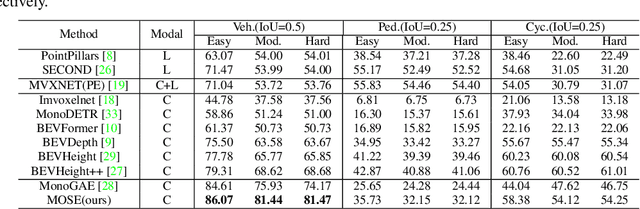
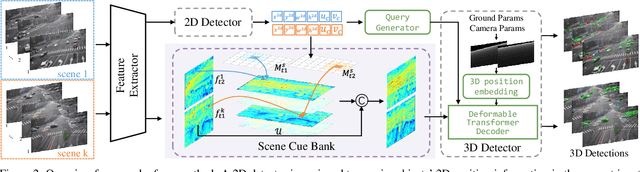
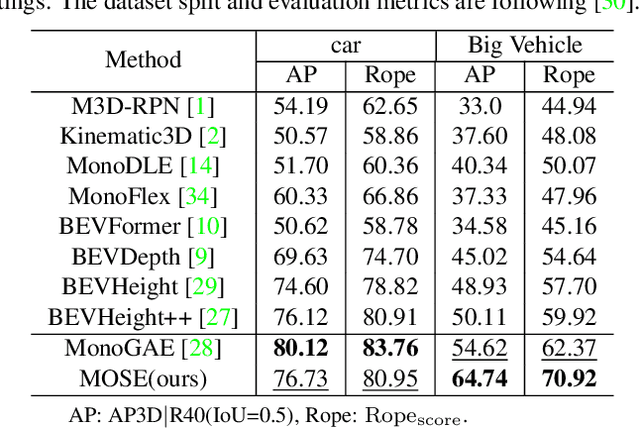
3D object detection based on roadside cameras is an additional way for autonomous driving to alleviate the challenges of occlusion and short perception range from vehicle cameras. Previous methods for roadside 3D object detection mainly focus on modeling the depth or height of objects, neglecting the stationary of cameras and the characteristic of inter-frame consistency. In this work, we propose a novel framework, namely MOSE, for MOnocular 3D object detection with Scene cuEs. The scene cues are the frame-invariant scene-specific features, which are crucial for object localization and can be intuitively regarded as the height between the surface of the real road and the virtual ground plane. In the proposed framework, a scene cue bank is designed to aggregate scene cues from multiple frames of the same scene with a carefully designed extrinsic augmentation strategy. Then, a transformer-based decoder lifts the aggregated scene cues as well as the 3D position embeddings for 3D object location, which boosts generalization ability in heterologous scenes. The extensive experiment results on two public benchmarks demonstrate the state-of-the-art performance of the proposed method, which surpasses the existing methods by a large margin.

On the Identifiability from Modulo Measurements under DFT Sensing Matrix

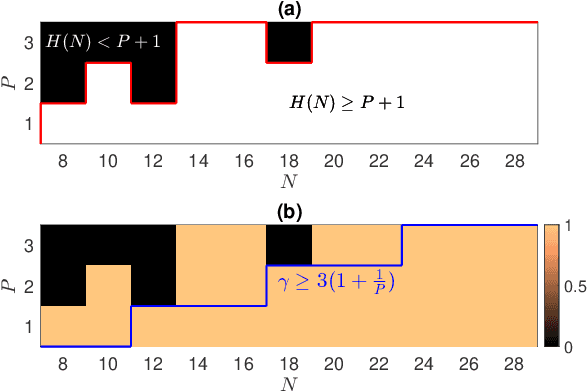
Unlimited sampling was recently introduced to deal with the clipping or saturation of measurements where a modulo operator is applied before sampling. In this paper, we investigate the identifiability of the model where measurements are acquired under a discrete Fourier transform (DFT) sensing matrix first followed by a modulo operator (modulo-DFT). Firstly, based on the theorems of cyclotomic polynomials, we derive a sufficient condition for uniquely identifying the original signal in modulo-DFT. Additionally, for periodic bandlimited signals (PBSs) under unlimited sampling which can be viewed as a special case of modulo-DFT, the necessary and sufficient condition for the unique recovery of the original signal are provided. Moreover, we show that when the oversampling factor exceeds $3(1+1/P)$, PBS is always identifiable from the modulo samples, where $P$ is the number of harmonics including the fundamental component in the positive frequency part.

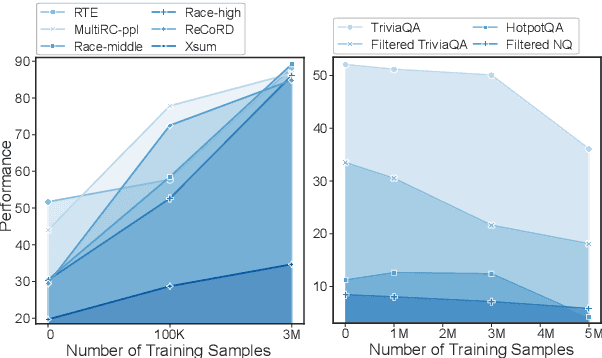
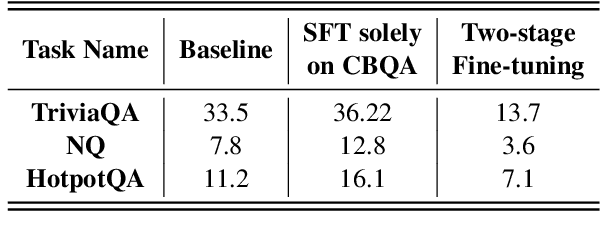
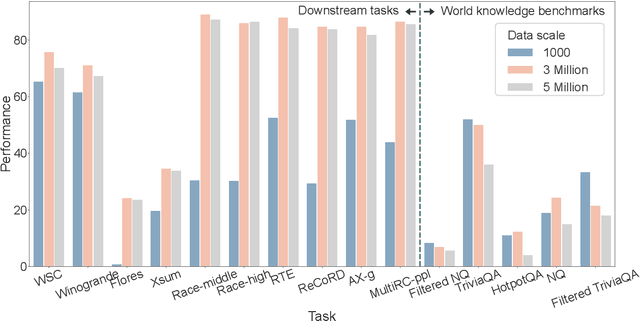
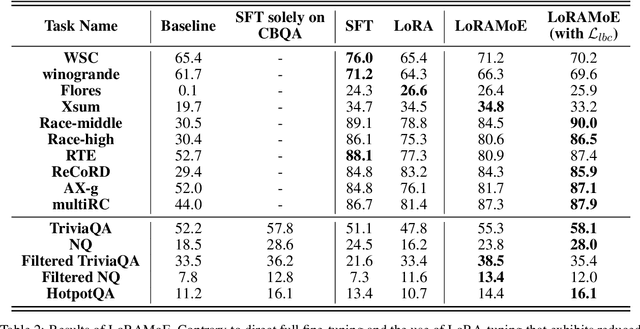
LoRAMoE: Revolutionizing Mixture of Experts for Maintaining World Knowledge in Language Model Alignment

Supervised fine-tuning (SFT) is a crucial step for large language models (LLMs), enabling them to align with human instructions and enhance their capabilities in downstream tasks. When the models are required to align with a broader range of downstream tasks, or there is a desire to notably improve the performance on a specific task, a substantial increase in fine-tuning data often emerges as the solution. However, we find that large-scale increases in instruction data can disrupt the world knowledge previously stored in the LLMs, i.e., world knowledge forgetting. In this paper, we introduce LoRAMoE to address the above challenge. The LoRAMoE is a plugin version of Mixture of Experts (MoE). The plugin form ensures the integrity of world knowledge by freezing the backbone model during the training phase. We then propose the use of localized balancing constraints to coordinate parts of experts for task utilization, meanwhile enabling other experts to fully leverage the world knowledge stored in the models. Experimental results demonstrate that LoRAMoE can reasonably coordinate experts based on data type during inference, and even dramatically increasing instruction data does not result in knowledge forgetting. Moreover, LoRAMoE provides additional benefits for the performance of downstream tasks, indicating the potential of our approach for multi-task learning.