Mobile Augmented Reality Framework with Fusional Localization and Pose Estimation

As a novel way of presenting information, augmented reality (AR) enables people to interact with the physical world in a direct and intuitive way. While there are some mobile AR products implemented with specific hardware at a high cost, the software approaches of AR implementation on mobile platforms(such as smartphones, tablet PC, etc.) are still far from practical use. GPS-based mobile AR systems usually perform poorly due to the inaccurate positioning in the indoor environment. Previous vision-based pose estimation methods need to continuously track predefined markers within a short distance, which greatly degrade user experience. This paper first conducts a comprehensive study of the state-of-the-art AR and localization systems on mobile platforms. Then, we propose an effective indoor mobile AR framework. In the framework, a fusional localization method and a new pose estimation implementation are developed to increase the overall matching rate and thus improving AR display accuracy. Experiments show that our framework has higher performance than approaches purely based on images or Wi-Fi signals. We achieve low average error distances (0.61-0.81m) and accurate matching rates (77%-82%) when the average sampling grid length is set to 0.5m.

Hyperbolic Chamfer Distance for Point Cloud Completion and Beyond

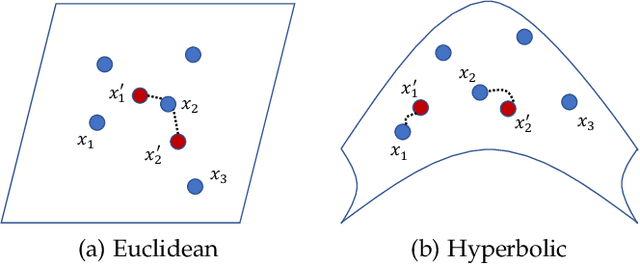
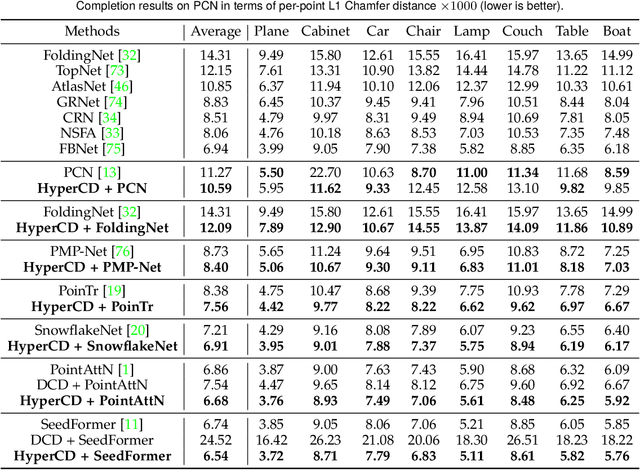
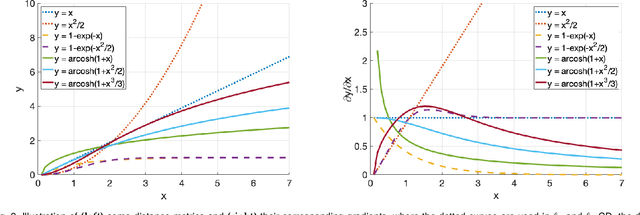
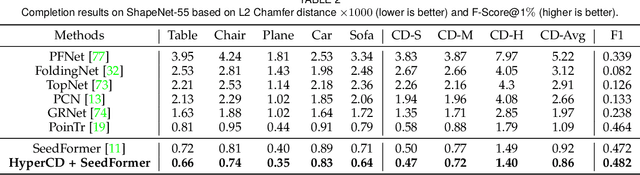
Chamfer Distance (CD) is widely used as a metric to quantify difference between two point clouds. In point cloud completion, Chamfer Distance (CD) is typically used as a loss function in deep learning frameworks. However, it is generally acknowledged within the field that Chamfer Distance (CD) is vulnerable to the presence of outliers, which can consequently lead to the convergence on suboptimal models. In divergence from the existing literature, which largely concentrates on resolving such concerns in the realm of Euclidean space, we put forth a notably uncomplicated yet potent metric specifically designed for point cloud completion tasks: {Hyperbolic Chamfer Distance (HyperCD)}. This metric conducts Chamfer Distance computations within the parameters of hyperbolic space. During the backpropagation process, HyperCD systematically allocates greater weight to matched point pairs exhibiting reduced Euclidean distances. This mechanism facilitates the preservation of accurate point pair matches while permitting the incremental adjustment of suboptimal matches, thereby contributing to enhanced point cloud completion outcomes. Moreover, measure the shape dissimilarity is not solely work for point cloud completion task, we further explore its applications in other generative related tasks, including single image reconstruction from point cloud, and upsampling. We demonstrate state-of-the-art performance on the point cloud completion benchmark datasets, PCN, ShapeNet-55, and ShapeNet-34, and show from visualization that HyperCD can significantly improve the surface smoothness, we also provide the provide experimental results beyond completion task.

SPADE: Spectroscopic Photoacoustic Denoising using an Analytical and Data-free Enhancement Framework

Spectroscopic photoacoustic (sPA) imaging uses multiple wavelengths to differentiate chromophores based on their unique optical absorption spectra. This technique has been widely applied in areas such as vascular mapping, tumor detection, and therapeutic monitoring. However, sPA imaging is highly susceptible to noise, leading to poor signal-to-noise ratio (SNR) and compromised image quality. Traditional denoising techniques like frame averaging, though effective in improving SNR, can be impractical for dynamic imaging scenarios due to reduced frame rates. Advanced methods, including learning-based approaches and analytical algorithms, have demonstrated promise but often require extensive training data and parameter tuning, limiting their adaptability for real-time clinical use. In this work, we propose a sPA denoising using a tuning-free analytical and data-free enhancement (SPADE) framework for denoising sPA images. This framework integrates a data-free learning-based method with an efficient BM3D-based analytical approach while preserves spectral linearity, providing noise reduction and ensuring that functional information is maintained. The SPADE framework was validated through simulation, phantom, ex vivo, and in vivo experiments. Results demonstrated that SPADE improved SNR and preserved spectral information, outperforming conventional methods, especially in challenging imaging conditions. SPADE presents a promising solution for enhancing sPA imaging quality in clinical applications where noise reduction and spectral preservation are critical.

Deep Loss Convexification for Learning Iterative Models

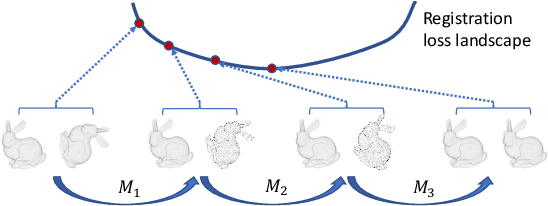
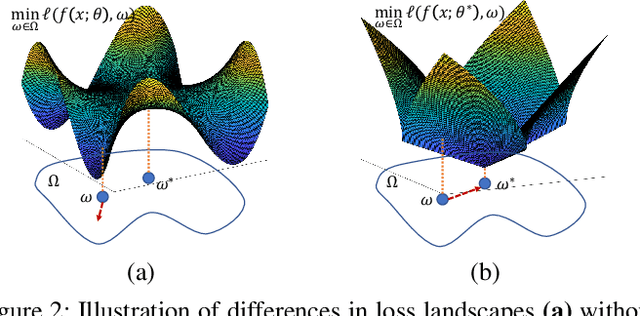
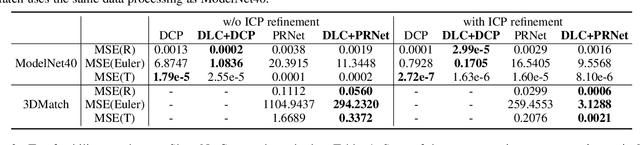
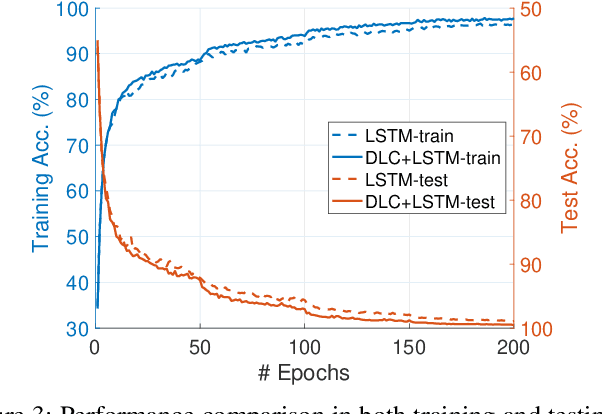
Iterative methods such as iterative closest point (ICP) for point cloud registration often suffer from bad local optimality (e.g. saddle points), due to the nature of nonconvex optimization. To address this fundamental challenge, in this paper we propose learning to form the loss landscape of a deep iterative method w.r.t. predictions at test time into a convex-like shape locally around each ground truth given data, namely Deep Loss Convexification (DLC), thanks to the overparametrization in neural networks. To this end, we formulate our learning objective based on adversarial training by manipulating the ground-truth predictions, rather than input data. In particular, we propose using star-convexity, a family of structured nonconvex functions that are unimodal on all lines that pass through a global minimizer, as our geometric constraint for reshaping loss landscapes, leading to (1) extra novel hinge losses appended to the original loss and (2) near-optimal predictions. We demonstrate the state-of-the-art performance using DLC with existing network architectures for the tasks of training recurrent neural networks (RNNs), 3D point cloud registration, and multimodel image alignment.

Loss Distillation via Gradient Matching for Point Cloud Completion with Weighted Chamfer Distance

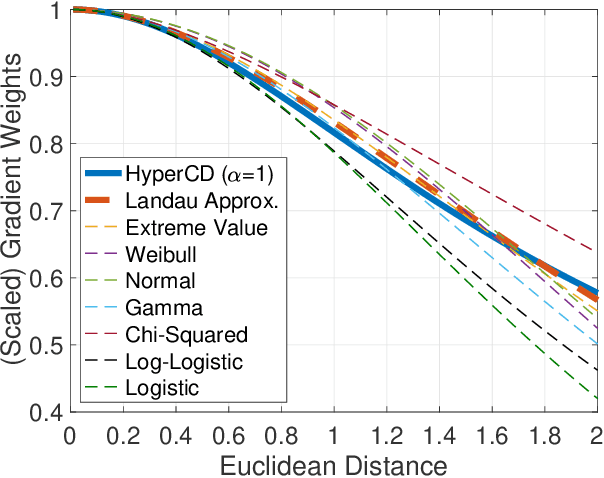
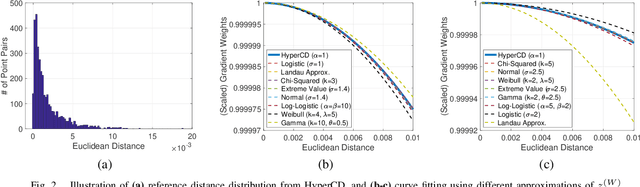
3D point clouds enhanced the robot's ability to perceive the geometrical information of the environments, making it possible for many downstream tasks such as grasp pose detection and scene understanding. The performance of these tasks, though, heavily relies on the quality of data input, as incomplete can lead to poor results and failure cases. Recent training loss functions designed for deep learning-based point cloud completion, such as Chamfer distance (CD) and its variants (\eg HyperCD ), imply a good gradient weighting scheme can significantly boost performance. However, these CD-based loss functions usually require data-related parameter tuning, which can be time-consuming for data-extensive tasks. To address this issue, we aim to find a family of weighted training losses ({\em weighted CD}) that requires no parameter tuning. To this end, we propose a search scheme, {\em Loss Distillation via Gradient Matching}, to find good candidate loss functions by mimicking the learning behavior in backpropagation between HyperCD and weighted CD. Once this is done, we propose a novel bilevel optimization formula to train the backbone network based on the weighted CD loss. We observe that: (1) with proper weighted functions, the weighted CD can always achieve similar performance to HyperCD, and (2) the Landau weighted CD, namely {\em Landau CD}, can outperform HyperCD for point cloud completion and lead to new state-of-the-art results on several benchmark datasets. {\it Our demo code is available at \url{https://github.com/Zhang-VISLab/IROS2024-LossDistillationWeightedCD}.}

Understanding Hyperbolic Metric Learning through Hard Negative Sampling

In recent years, there has been a growing trend of incorporating hyperbolic geometry methods into computer vision. While these methods have achieved state-of-the-art performance on various metric learning tasks using hyperbolic distance measurements, the underlying theoretical analysis supporting this superior performance remains under-exploited. In this study, we investigate the effects of integrating hyperbolic space into metric learning, particularly when training with contrastive loss. We identify a need for a comprehensive comparison between Euclidean and hyperbolic spaces regarding the temperature effect in the contrastive loss within the existing literature. To address this gap, we conduct an extensive investigation to benchmark the results of Vision Transformers (ViTs) using a hybrid objective function that combines loss from Euclidean and hyperbolic spaces. Additionally, we provide a theoretical analysis of the observed performance improvement. We also reveal that hyperbolic metric learning is highly related to hard negative sampling, providing insights for future work. This work will provide valuable data points and experience in understanding hyperbolic image embeddings. To shed more light on problem-solving and encourage further investigation into our approach, our code is available online (https://github.com/YunYunY/HypMix).

Hyperbolic Contrastive Learning

Learning good image representations that are beneficial to downstream tasks is a challenging task in computer vision. As such, a wide variety of self-supervised learning approaches have been proposed. Among them, contrastive learning has shown competitive performance on several benchmark datasets. The embeddings of contrastive learning are arranged on a hypersphere that results in using the inner (dot) product as a distance measurement in Euclidean space. However, the underlying structure of many scientific fields like social networks, brain imaging, and computer graphics data exhibit highly non-Euclidean latent geometry. We propose a novel contrastive learning framework to learn semantic relationships in the hyperbolic space. Hyperbolic space is a continuous version of trees that naturally owns the ability to model hierarchical structures and is thus beneficial for efficient contrastive representation learning. We also extend the proposed Hyperbolic Contrastive Learning (HCL) to the supervised domain and studied the adversarial robustness of HCL. The comprehensive experiments show that our proposed method achieves better results on self-supervised pretraining, supervised classification, and higher robust accuracy than baseline methods.

FPCC-Net: Fast Point Cloud Clustering for Instance Segmentation

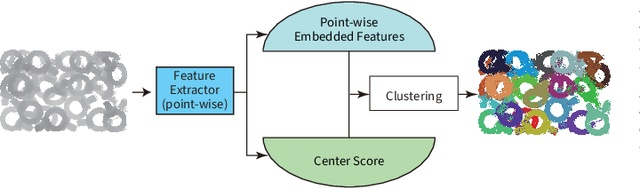
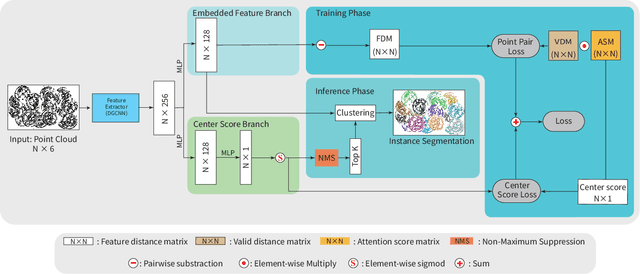
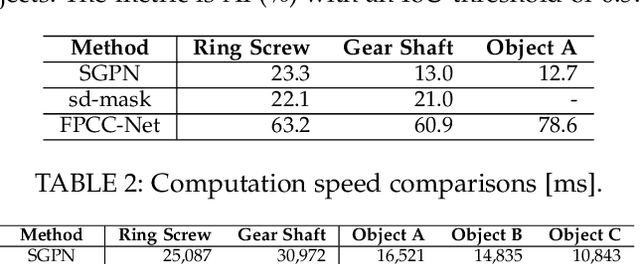
Instance segmentation is an important pre-processing task in numerous real-world applications, such as robotics, autonomous vehicles, and human-computer interaction. However, there has been little research on 3D point cloud instance segmentation of bin-picking scenes in which multiple objects of the same class are stacked together. Compared with the rapid development of deep learning for two-dimensional (2D) image tasks, deep learning-based 3D point cloud segmentation still has a lot of room for development. In such a situation, distinguishing a large number of occluded objects of the same class is a highly challenging problem. In a usual bin-picking scene, an object model is known and the number of object type is one. Thus, the semantic information can be ignored; instead, the focus is put on the segmentation of instances. Based on this task requirement, we propose a network (FPCC-Net) that infers feature centers of each instance and then clusters the remaining points to the closest feature center in feature embedding space. FPCC-Net includes two subnets, one for inferring the feature centers for clustering and the other for describing features of each point. The proposed method is compared with existing 3D point cloud and 2D segmentation methods in some bin-picking scenes. It is shown that FPCC-Net improves average precision (AP) by about 40\% than SGPN and can process about 60,000 points in about 0.8 [s].