Multi-Agent Deep Research: Training Multi-Agent Systems with M-GRPO

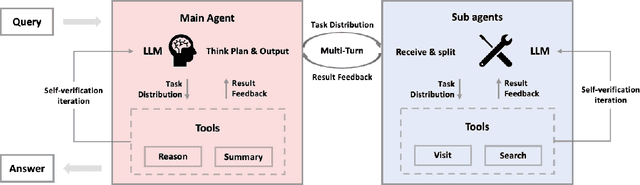
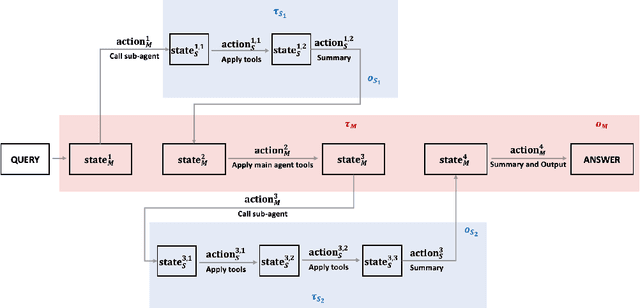
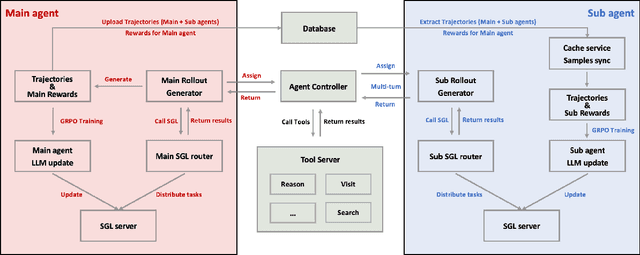
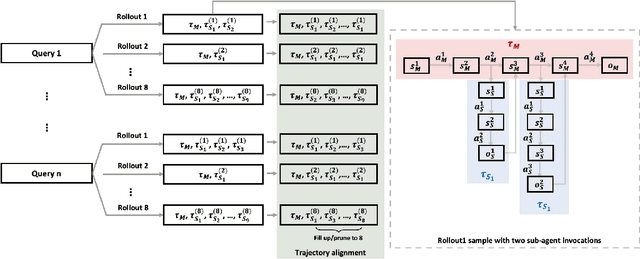
Multi-agent systems perform well on general reasoning tasks. However, the lack of training in specialized areas hinders their accuracy. Current training methods train a unified large language model (LLM) for all agents in the system. This may limit the performances due to different distributions underlying for different agents. Therefore, training multi-agent systems with distinct LLMs should be the next step to solve. However, this approach introduces optimization challenges. For example, agents operate at different frequencies, rollouts involve varying sub-agent invocations, and agents are often deployed across separate servers, disrupting end-to-end gradient flow. To address these issues, we propose M-GRPO, a hierarchical extension of Group Relative Policy Optimization designed for vertical Multi-agent systems with a main agent (planner) and multiple sub-agents (multi-turn tool executors). M-GRPO computes group-relative advantages for both main and sub-agents, maintaining hierarchical credit assignment. It also introduces a trajectory-alignment scheme that generates fixed-size batches despite variable sub-agent invocations. We deploy a decoupled training pipeline in which agents run on separate servers and exchange minimal statistics via a shared store. This enables scalable training without cross-server backpropagation. In experiments on real-world benchmarks (e.g., GAIA, XBench-DeepSearch, and WebWalkerQA), M-GRPO consistently outperforms both single-agent GRPO and multi-agent GRPO with frozen sub-agents, demonstrating improved stability and sample efficiency. These results show that aligning heterogeneous trajectories and decoupling optimization across specialized agents enhances tool-augmented reasoning tasks.

MedReseacher-R1: Expert-Level Medical Deep Researcher via A Knowledge-Informed Trajectory Synthesis Framework

Recent developments in Large Language Model (LLM)-based agents have shown impressive capabilities spanning multiple domains, exemplified by deep research systems that demonstrate superior performance on complex information-seeking and synthesis tasks. While general-purpose deep research agents have shown impressive capabilities, they struggle significantly with medical domain challenges, as evidenced by leading proprietary systems achieving limited accuracy on complex medical benchmarks. The key limitations are: (1) the model lacks sufficient dense medical knowledge for clinical reasoning, and (2) the framework is constrained by the absence of specialized retrieval tools tailored for medical contexts.We present a medical deep research agent that addresses these challenges through two core innovations. First, we develop a novel data synthesis framework using medical knowledge graphs, extracting the longest chains from subgraphs around rare medical entities to generate complex multi-hop question-answer pairs. Second, we integrate a custom-built private medical retrieval engine alongside general-purpose tools, enabling accurate medical information synthesis. Our approach generates 2100+ diverse trajectories across 12 medical specialties, each averaging 4.2 tool interactions.Through a two-stage training paradigm combining supervised fine-tuning and online reinforcement learning with composite rewards, our MedResearcher-R1-32B model demonstrates exceptional performance, establishing new state-of-the-art results on medical benchmarks while maintaining competitive performance on general deep research tasks. Our work demonstrates that strategic domain-specific innovations in architecture, tool design, and training data construction can enable smaller open-source models to outperform much larger proprietary systems in specialized domains.

Learning to Align, Aligning to Learn: A Unified Approach for Self-Optimized Alignment

Alignment methodologies have emerged as a critical pathway for enhancing language model alignment capabilities. While SFT (supervised fine-tuning) accelerates convergence through direct token-level loss intervention, its efficacy is constrained by offline policy trajectory. In contrast, RL(reinforcement learning) facilitates exploratory policy optimization, but suffers from low sample efficiency and stringent dependency on high-quality base models. To address these dual challenges, we propose GRAO (Group Relative Alignment Optimization), a unified framework that synergizes the respective strengths of SFT and RL through three key innovations: 1) A multi-sample generation strategy enabling comparative quality assessment via reward feedback; 2) A novel Group Direct Alignment Loss formulation leveraging intra-group relative advantage weighting; 3) Reference-aware parameter updates guided by pairwise preference dynamics. Our theoretical analysis establishes GRAO's convergence guarantees and sample efficiency advantages over conventional approaches. Comprehensive evaluations across complex human alignment tasks demonstrate GRAO's superior performance, achieving 57.70\%,17.65\% 7.95\% and 5.18\% relative improvements over SFT, DPO, PPO and GRPO baselines respectively. This work provides both a theoretically grounded alignment framework and empirical evidence for efficient capability evolution in language models.

EDiT: A Local-SGD-Based Efficient Distributed Training Method for Large Language Models

Distributed training methods are crucial for large language models (LLMs). However, existing distributed training methods often suffer from communication bottlenecks, stragglers, and limited elasticity. Local SGD methods have been proposed to address these issues, but their effectiveness remains limited to small-scale training due to additional memory overhead and lack of concerns on efficiency and stability. To tackle these issues, we propose EDiT, an innovative Efficient Distributed Training method that combines a tailored Local SGD approach with model sharding techniques to enhance large-scale training efficiency. EDiT performs layer-wise parameter synchronization during forward pass, reducing communication and memory overhead and enabling the overlap of computation and communication. Besides, EDiT employs a pseudo gradient penalty strategy to suppress loss spikes, which ensures training stability and improve performance. Additionally, we introduce A-EDiT, a fully asynchronous variant of EDiT that accommodates heterogeneous clusters. Building on EDiT/A-EDiT, we conduct a series of experiments to validate large-scale asynchronous training for LLMs, accompanied by comprehensive analyses. Experimental results demonstrate the superior performance of EDiT/A-EDiT, establishing them as robust solutions for distributed LLM training in diverse computational ecosystems.

Wildlife Product Trading in Online Social Networks: A Case Study on Ivory-Related Product Sales Promotion Posts

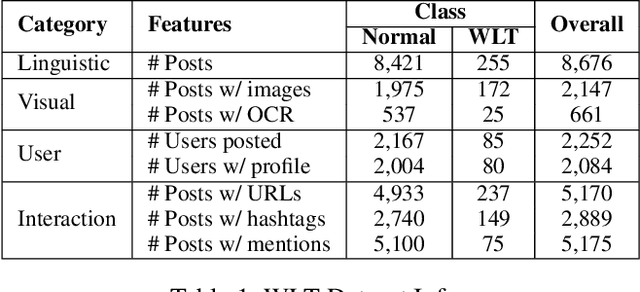
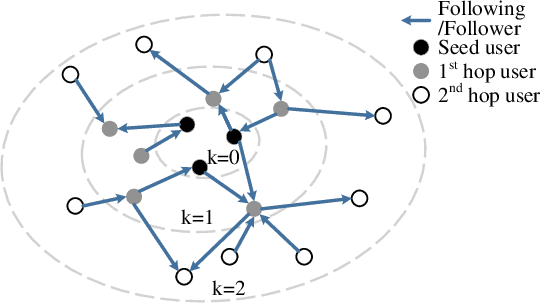
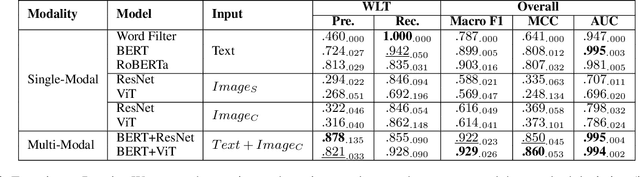
Wildlife trafficking (WLT) has emerged as a global issue, with traffickers expanding their operations from offline to online platforms, utilizing e-commerce websites and social networks to enhance their illicit trade. This paper addresses the challenge of detecting and recognizing wildlife product sales promotion behaviors in online social networks, a crucial aspect in combating these environmentally harmful activities. To counter these environmentally damaging illegal operations, in this research, we focus on wildlife product sales promotion behaviors in online social networks. Specifically, 1) A scalable dataset related to wildlife product trading is collected using a network-based approach. This dataset is labeled through a human-in-the-loop machine learning process, distinguishing positive class samples containing wildlife product selling posts and hard-negatives representing normal posts misclassified as potential WLT posts, subsequently corrected by human annotators. 2) We benchmark the machine learning results on the proposed dataset and build a practical framework that automatically identifies suspicious wildlife selling posts and accounts, sufficiently leveraging the multi-modal nature of online social networks. 3) This research delves into an in-depth analysis of trading posts, shedding light on the systematic and organized selling behaviors prevalent in the current landscape. We provide detailed insights into the nature of these behaviors, contributing valuable information for understanding and countering illegal wildlife product trading.

Understanding Hyperbolic Metric Learning through Hard Negative Sampling

In recent years, there has been a growing trend of incorporating hyperbolic geometry methods into computer vision. While these methods have achieved state-of-the-art performance on various metric learning tasks using hyperbolic distance measurements, the underlying theoretical analysis supporting this superior performance remains under-exploited. In this study, we investigate the effects of integrating hyperbolic space into metric learning, particularly when training with contrastive loss. We identify a need for a comprehensive comparison between Euclidean and hyperbolic spaces regarding the temperature effect in the contrastive loss within the existing literature. To address this gap, we conduct an extensive investigation to benchmark the results of Vision Transformers (ViTs) using a hybrid objective function that combines loss from Euclidean and hyperbolic spaces. Additionally, we provide a theoretical analysis of the observed performance improvement. We also reveal that hyperbolic metric learning is highly related to hard negative sampling, providing insights for future work. This work will provide valuable data points and experience in understanding hyperbolic image embeddings. To shed more light on problem-solving and encourage further investigation into our approach, our code is available online (https://github.com/YunYunY/HypMix).

AGD: an Auto-switchable Optimizer using Stepwise Gradient Difference for Preconditioning Matrix

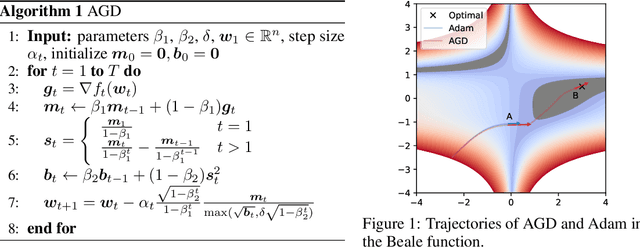
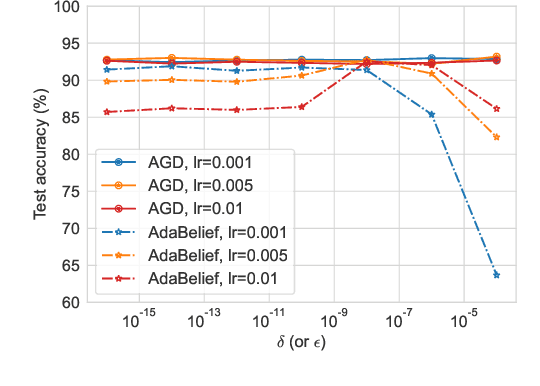
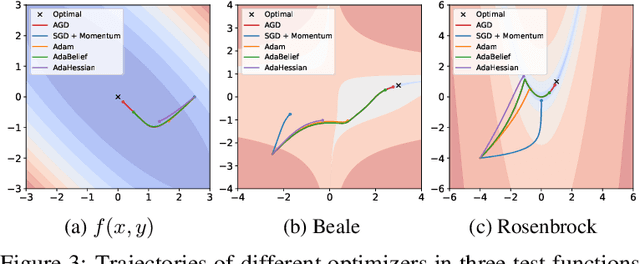
Adaptive optimizers, such as Adam, have achieved remarkable success in deep learning. A key component of these optimizers is the so-called preconditioning matrix, providing enhanced gradient information and regulating the step size of each gradient direction. In this paper, we propose a novel approach to designing the preconditioning matrix by utilizing the gradient difference between two successive steps as the diagonal elements. These diagonal elements are closely related to the Hessian and can be perceived as an approximation of the inner product between the Hessian row vectors and difference of the adjacent parameter vectors. Additionally, we introduce an auto-switching function that enables the preconditioning matrix to switch dynamically between Stochastic Gradient Descent (SGD) and the adaptive optimizer. Based on these two techniques, we develop a new optimizer named AGD that enhances the generalization performance. We evaluate AGD on public datasets of Natural Language Processing (NLP), Computer Vision (CV), and Recommendation Systems (RecSys). Our experimental results demonstrate that AGD outperforms the state-of-the-art (SOTA) optimizers, achieving highly competitive or significantly better predictive performance. Furthermore, we analyze how AGD is able to switch automatically between SGD and the adaptive optimizer and its actual effects on various scenarios. The code is available at https://github.com/intelligent-machine-learning/dlrover/tree/master/atorch/atorch/optimizers.

Sharpness-Aware Minimization Revisited: Weighted Sharpness as a Regularization Term

Deep Neural Networks (DNNs) generalization is known to be closely related to the flatness of minima, leading to the development of Sharpness-Aware Minimization (SAM) for seeking flatter minima and better generalization. In this paper, we revisit the loss of SAM and propose a more general method, called WSAM, by incorporating sharpness as a regularization term. We prove its generalization bound through the combination of PAC and Bayes-PAC techniques, and evaluate its performance on various public datasets. The results demonstrate that WSAM achieves improved generalization, or is at least highly competitive, compared to the vanilla optimizer, SAM and its variants. The code is available at https://github.com/intelligent-machine-learning/dlrover/tree/master/atorch/atorch/optimizers.

Hyperbolic Contrastive Learning

Learning good image representations that are beneficial to downstream tasks is a challenging task in computer vision. As such, a wide variety of self-supervised learning approaches have been proposed. Among them, contrastive learning has shown competitive performance on several benchmark datasets. The embeddings of contrastive learning are arranged on a hypersphere that results in using the inner (dot) product as a distance measurement in Euclidean space. However, the underlying structure of many scientific fields like social networks, brain imaging, and computer graphics data exhibit highly non-Euclidean latent geometry. We propose a novel contrastive learning framework to learn semantic relationships in the hyperbolic space. Hyperbolic space is a continuous version of trees that naturally owns the ability to model hierarchical structures and is thus beneficial for efficient contrastive representation learning. We also extend the proposed Hyperbolic Contrastive Learning (HCL) to the supervised domain and studied the adversarial robustness of HCL. The comprehensive experiments show that our proposed method achieves better results on self-supervised pretraining, supervised classification, and higher robust accuracy than baseline methods.

Adaptive Optimizers with Sparse Group Lasso for Neural Networks in CTR Prediction

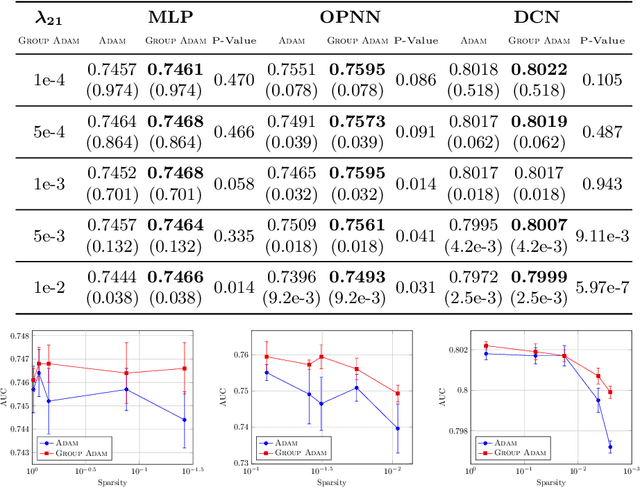
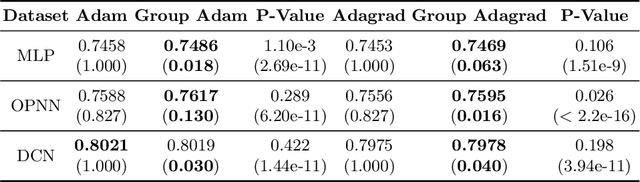
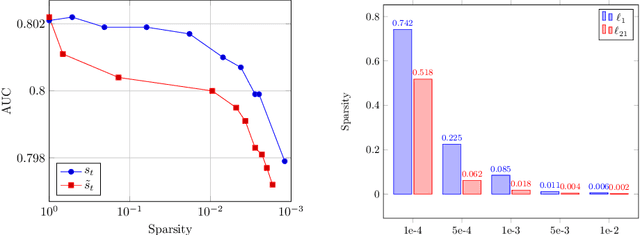
We develop a novel framework that adds the regularizers of the sparse group lasso to a family of adaptive optimizers in deep learning, such as Momentum, Adagrad, Adam, AMSGrad, AdaHessian, and create a new class of optimizers, which are named Group Momentum, Group Adagrad, Group Adam, Group AMSGrad and Group AdaHessian, etc., accordingly. We establish theoretically proven convergence guarantees in the stochastic convex settings, based on primal-dual methods. We evaluate the regularized effect of our new optimizers on three large-scale real-world ad click datasets with state-of-the-art deep learning models. The experimental results reveal that compared with the original optimizers with the post-processing procedure which uses the magnitude pruning method, the performance of the models can be significantly improved on the same sparsity level. Furthermore, in comparison to the cases without magnitude pruning, our methods can achieve extremely high sparsity with significantly better or highly competitive performance.