Chunyang Wen
Adaptive Optimizers with Sparse Group Lasso for Neural Networks in CTR Prediction
Jul 30, 2021
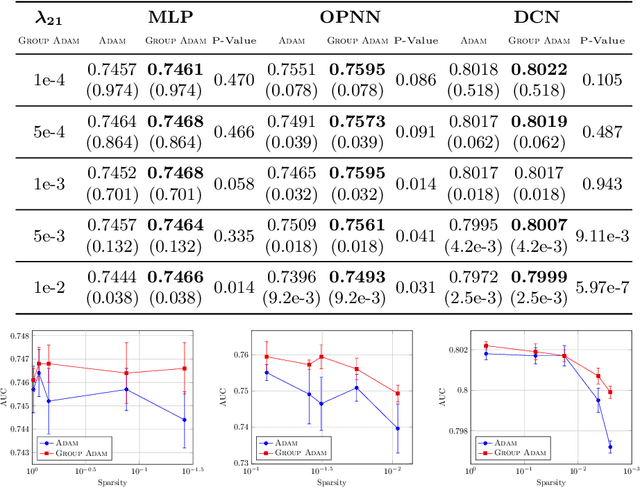
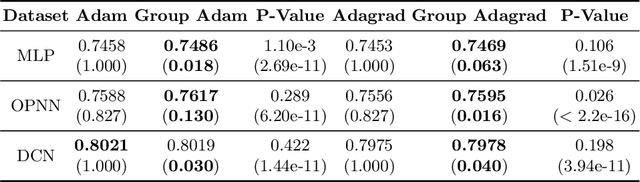
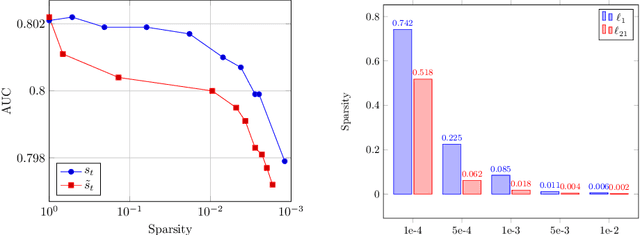
Abstract:We develop a novel framework that adds the regularizers of the sparse group lasso to a family of adaptive optimizers in deep learning, such as Momentum, Adagrad, Adam, AMSGrad, AdaHessian, and create a new class of optimizers, which are named Group Momentum, Group Adagrad, Group Adam, Group AMSGrad and Group AdaHessian, etc., accordingly. We establish theoretically proven convergence guarantees in the stochastic convex settings, based on primal-dual methods. We evaluate the regularized effect of our new optimizers on three large-scale real-world ad click datasets with state-of-the-art deep learning models. The experimental results reveal that compared with the original optimizers with the post-processing procedure which uses the magnitude pruning method, the performance of the models can be significantly improved on the same sparsity level. Furthermore, in comparison to the cases without magnitude pruning, our methods can achieve extremely high sparsity with significantly better or highly competitive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge