Hyperbolic Chamfer Distance for Point Cloud Completion and Beyond
Paper and Code
Dec 23, 2024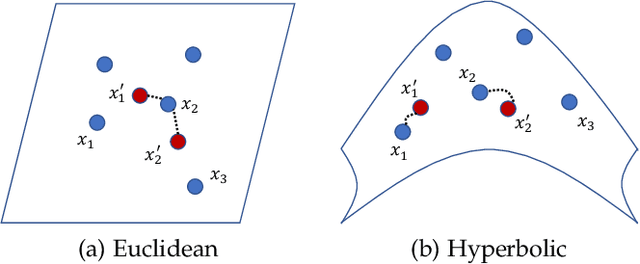
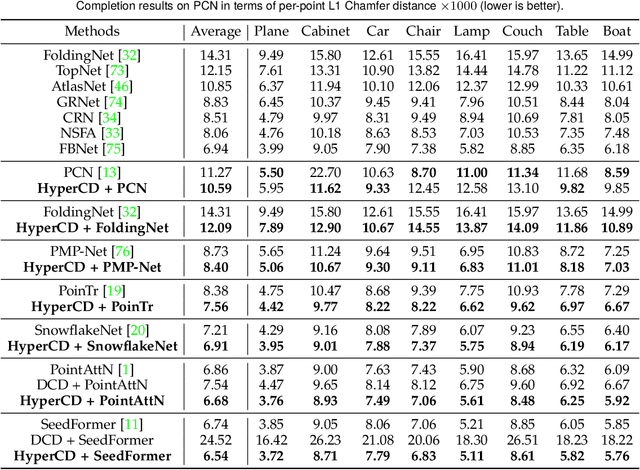
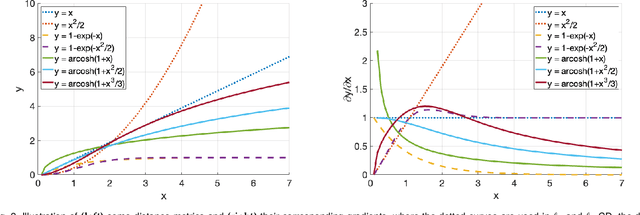
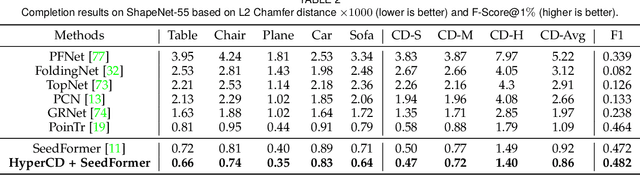
Chamfer Distance (CD) is widely used as a metric to quantify difference between two point clouds. In point cloud completion, Chamfer Distance (CD) is typically used as a loss function in deep learning frameworks. However, it is generally acknowledged within the field that Chamfer Distance (CD) is vulnerable to the presence of outliers, which can consequently lead to the convergence on suboptimal models. In divergence from the existing literature, which largely concentrates on resolving such concerns in the realm of Euclidean space, we put forth a notably uncomplicated yet potent metric specifically designed for point cloud completion tasks: {Hyperbolic Chamfer Distance (HyperCD)}. This metric conducts Chamfer Distance computations within the parameters of hyperbolic space. During the backpropagation process, HyperCD systematically allocates greater weight to matched point pairs exhibiting reduced Euclidean distances. This mechanism facilitates the preservation of accurate point pair matches while permitting the incremental adjustment of suboptimal matches, thereby contributing to enhanced point cloud completion outcomes. Moreover, measure the shape dissimilarity is not solely work for point cloud completion task, we further explore its applications in other generative related tasks, including single image reconstruction from point cloud, and upsampling. We demonstrate state-of-the-art performance on the point cloud completion benchmark datasets, PCN, ShapeNet-55, and ShapeNet-34, and show from visualization that HyperCD can significantly improve the surface smoothness, we also provide the provide experimental results beyond completion task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge