Understanding and Addressing the Pitfalls of Bisimulation-based Representations in Offline Reinforcement Learning

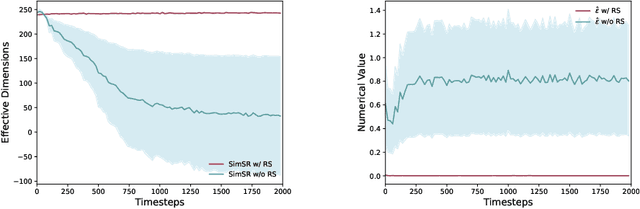
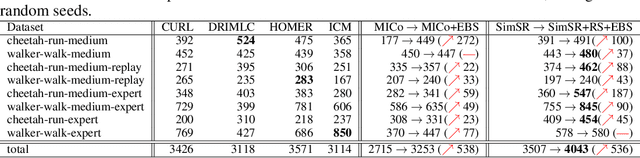
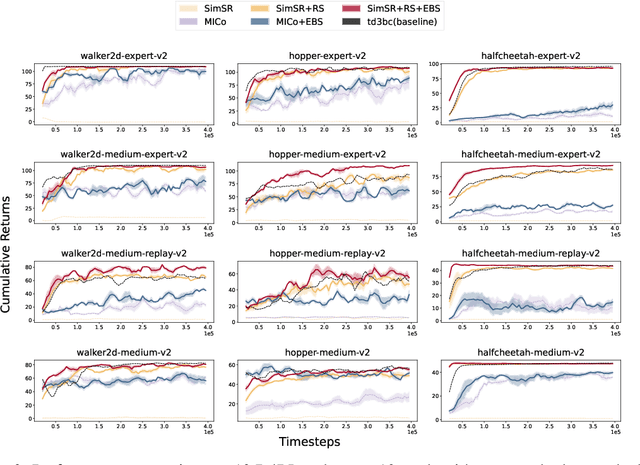
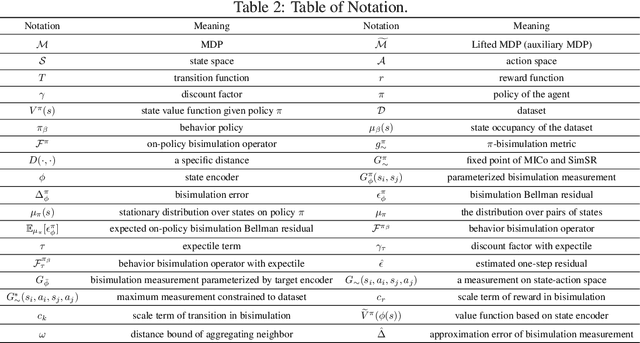
While bisimulation-based approaches hold promise for learning robust state representations for Reinforcement Learning (RL) tasks, their efficacy in offline RL tasks has not been up to par. In some instances, their performance has even significantly underperformed alternative methods. We aim to understand why bisimulation methods succeed in online settings, but falter in offline tasks. Our analysis reveals that missing transitions in the dataset are particularly harmful to the bisimulation principle, leading to ineffective estimation. We also shed light on the critical role of reward scaling in bounding the scale of bisimulation measurements and of the value error they induce. Based on these findings, we propose to apply the expectile operator for representation learning to our offline RL setting, which helps to prevent overfitting to incomplete data. Meanwhile, by introducing an appropriate reward scaling strategy, we avoid the risk of feature collapse in representation space. We implement these recommendations on two state-of-the-art bisimulation-based algorithms, MICo and SimSR, and demonstrate performance gains on two benchmark suites: D4RL and Visual D4RL. Codes are provided at \url{https://github.com/zanghyu/Offline_Bisimulation}.

Agent-Controller Representations: Principled Offline RL with Rich Exogenous Information

Learning to control an agent from data collected offline in a rich pixel-based visual observation space is vital for real-world applications of reinforcement learning (RL). A major challenge in this setting is the presence of input information that is hard to model and irrelevant to controlling the agent. This problem has been approached by the theoretical RL community through the lens of exogenous information, i.e, any control-irrelevant information contained in observations. For example, a robot navigating in busy streets needs to ignore irrelevant information, such as other people walking in the background, textures of objects, or birds in the sky. In this paper, we focus on the setting with visually detailed exogenous information, and introduce new offline RL benchmarks offering the ability to study this problem. We find that contemporary representation learning techniques can fail on datasets where the noise is a complex and time dependent process, which is prevalent in practical applications. To address these, we propose to use multi-step inverse models, which have seen a great deal of interest in the RL theory community, to learn Agent-Controller Representations for Offline-RL (ACRO). Despite being simple and requiring no reward, we show theoretically and empirically that the representation created by this objective greatly outperforms baselines.

Incorporating Explicit Uncertainty Estimates into Deep Offline Reinforcement Learning

Most theoretically motivated work in the offline reinforcement learning setting requires precise uncertainty estimates. This requirement restricts the algorithms derived in that work to the tabular and linear settings where such estimates exist. In this work, we develop a novel method for incorporating scalable uncertainty estimates into an offline reinforcement learning algorithm called deep-SPIBB that extends the SPIBB family of algorithms to environments with larger state and action spaces. We use recent innovations in uncertainty estimation from the deep learning community to get more scalable uncertainty estimates to plug into deep-SPIBB. While these uncertainty estimates do not allow for the same theoretical guarantees as in the tabular case, we argue that the SPIBB mechanism for incorporating uncertainty is more robust and flexible than pessimistic approaches that incorporate the uncertainty as a value function penalty. We bear this out empirically, showing that deep-SPIBB outperforms pessimism based approaches with access to the same uncertainty estimates and performs at least on par with a variety of other strong baselines across several environments and datasets.

Non-Markovian policies occupancy measures

A central object of study in Reinforcement Learning (RL) is the Markovian policy, in which an agent's actions are chosen from a memoryless probability distribution, conditioned only on its current state. The family of Markovian policies is broad enough to be interesting, yet simple enough to be amenable to analysis. However, RL often involves more complex policies: ensembles of policies, policies over options, policies updated online, etc. Our main contribution is to prove that the occupancy measure of any non-Markovian policy, i.e., the distribution of transition samples collected with it, can be equivalently generated by a Markovian policy. This result allows theorems about the Markovian policy class to be directly extended to its non-Markovian counterpart, greatly simplifying proofs, in particular those involving replay buffers and datasets. We provide various examples of such applications to the field of Reinforcement Learning.

On the Regularity of Attention

Attention is a powerful component of modern neural networks across a wide variety of domains. In this paper, we seek to quantify the regularity (i.e. the amount of smoothness) of the attention operation. To accomplish this goal, we propose a new mathematical framework that uses measure theory and integral operators to model attention. We show that this framework is consistent with the usual definition, and that it captures the essential properties of attention. Then we use this framework to prove that, on compact domains, the attention operation is Lipschitz continuous and provide an estimate of its Lipschitz constant. Additionally, by focusing on a specific type of attention, we extend these Lipschitz continuity results to non-compact domains. We also discuss the effects regularity can have on NLP models, and applications to invertible and infinitely-deep networks.

A Deeper Look at Discounting Mismatch in Actor-Critic Algorithms

We investigate the discounting mismatch in actor-critic algorithm implementations from a representation learning perspective. Theoretically, actor-critic algorithms usually have discounting for both actor and critic, i.e., there is a $\gamma^t$ term in the actor update for the transition observed at time $t$ in a trajectory and the critic is a discounted value function. Practitioners, however, usually ignore the discounting ($\gamma^t$) for the actor while using a discounted critic. We investigate this mismatch in two scenarios. In the first scenario, we consider optimizing an undiscounted objective $(\gamma = 1)$ where $\gamma^t$ disappears naturally $(1^t = 1)$. We then propose to interpret the discounting in critic in terms of a bias-variance-representation trade-off and provide supporting empirical results. In the second scenario, we consider optimizing a discounted objective ($\gamma < 1$) and propose to interpret the omission of the discounting in the actor update from an auxiliary task perspective and provide supporting empirical results.

A Mathematical Theory of Attention

Attention is a powerful component of modern neural networks across a wide variety of domains. However, despite its ubiquity in machine learning, there is a gap in our understanding of attention from a theoretical point of view. We propose a framework to fill this gap by building a mathematically equivalent model of attention using measure theory. With this model, we are able to interpret self-attention as a system of self-interacting particles, we shed light on self-attention from a maximum entropy perspective, and we show that attention is actually Lipschitz-continuous (with an appropriate metric) under suitable assumptions. We then apply these insights to the problem of mis-specified input data; infinitely-deep, weight-sharing self-attention networks; and more general Lipschitz estimates for a specific type of attention studied in concurrent work.

Deep Reinforcement and InfoMax Learning

Our work is based on the hypothesis that a model-free agent whose representations are predictive of properties of future states (beyond expected rewards) will be more capable of solving and adapting to new RL problems. To test that hypothesis, we introduce an objective based on Deep InfoMax (DIM) which trains the agent to predict the future by maximizing the mutual information between its internal representation of successive timesteps. We provide an intuitive analysis of the convergence properties of our approach from the perspective of Markov chain mixing times and argue that convergence of the lower bound on mutual information is related to the inverse absolute spectral gap of the transition model. We test our approach in several synthetic settings, where it successfully learns representations that are predictive of the future. Finally, we augment C51, a strong RL baseline, with our temporal DIM objective and demonstrate improved performance on a continual learning task and on the recently introduced Procgen environment.

Domain Adaptation with Conditional Distribution Matching and Generalized Label Shift

Adversarial learning has demonstrated good performance in the unsupervised domain adaptation setting, by learning domain-invariant representations that perform well on the source domain. However, recent work has underlined limitations of existing methods in the presence of mismatched label distributions between the source and target domains. In this paper, we extend a recent upper-bound on the performance of adversarial domain adaptation to multi-class classification and more general discriminators. We then propose generalized label shift (GLS) as a way to improve robustness against mismatched label distributions. GLS states that, conditioned on the label, there exists a representation of the input that is invariant between the source and target domains. Under GLS, we provide theoretical guarantees on the transfer performance of any classifier. We also devise necessary and sufficient conditions for GLS to hold. The conditions are based on the estimation of the relative class weights between domains and on an appropriate reweighting of samples. Guided by our theoretical insights, we modify three widely used algorithms, JAN, DANN and CDAN and evaluate their performance on standard domain adaptation tasks where our method outperforms the base versions. We also demonstrate significant gains on artificially created tasks with large divergences between their source and target label distributions.

A Reduction from Reinforcement Learning to No-Regret Online Learning

We present a reduction from reinforcement learning (RL) to no-regret online learning based on the saddle-point formulation of RL, by which "any" online algorithm with sublinear regret can generate policies with provable performance guarantees. This new perspective decouples the RL problem into two parts: regret minimization and function approximation. The first part admits a standard online-learning analysis, and the second part can be quantified independently of the learning algorithm. Therefore, the proposed reduction can be used as a tool to systematically design new RL algorithms. We demonstrate this idea by devising a simple RL algorithm based on mirror descent and the generative-model oracle. For any $\gamma$-discounted tabular RL problem, with probability at least $1-\delta$, it learns an $\epsilon$-optimal policy using at most $\tilde{O}\left(\frac{|\mathcal{S}||\mathcal{A}|\log(\frac{1}{\delta})}{(1-\gamma)^4\epsilon^2}\right)$ samples. Furthermore, this algorithm admits a direct extension to linearly parameterized function approximators for large-scale applications, with computation and sample complexities independent of $|\mathcal{S}|$,$|\mathcal{A}|$, though at the cost of potential approximation bias.