Conformal Transformations for Symmetric Power Transformers

Transformers with linear attention offer significant computational advantages over softmax-based transformers but often suffer from degraded performance. The symmetric power (sympow) transformer, a particular type of linear transformer, addresses some of this performance gap by leveraging symmetric tensor embeddings, achieving comparable performance to softmax transformers. However, the finite capacity of the recurrent state in sympow transformers limits their ability to retain information, leading to performance degradation when scaling the training or evaluation context length. To address this issue, we propose the conformal-sympow transformer, which dynamically frees up capacity using data-dependent multiplicative gating and adaptively stores information using data-dependent rotary embeddings. Preliminary experiments on the LongCrawl64 dataset demonstrate that conformal-sympow overcomes the limitations of sympow transformers, achieving robust performance across scaled training and evaluation contexts.

Deep Autoregressive Regression

In this work, we demonstrate that a major limitation of regression using a mean-squared error loss is its sensitivity to the scale of its targets. This makes learning settings consisting of several subtasks with differently-scaled targets challenging, and causes algorithms to require task-specific learning rate tuning. A recently-proposed alternative loss function, known as histogram loss, avoids this issue. However, its computational cost grows linearly with the number of buckets in the histogram, which renders prediction with real-valued targets intractable. To address this issue, we propose a novel approach to training deep learning models on real-valued regression targets, autoregressive regression, which learns a high-fidelity distribution by utilizing an autoregressive target decomposition. We demonstrate that this training objective allows us to solve regression tasks involving multiple targets with different scales.

When does return-conditioned supervised learning work for offline reinforcement learning?

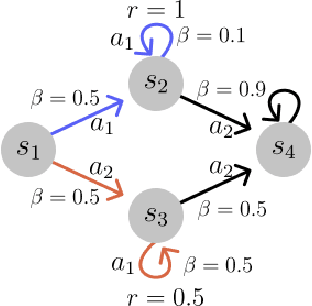
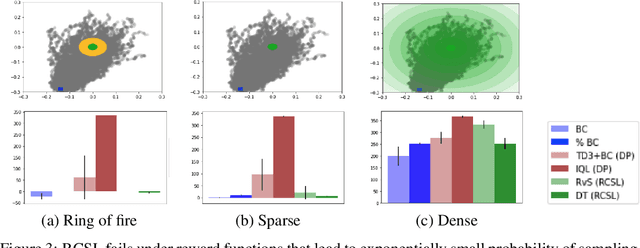
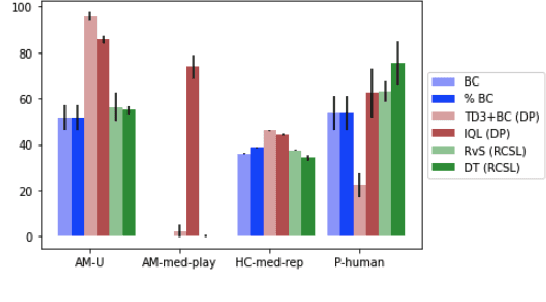
Several recent works have proposed a class of algorithms for the offline reinforcement learning (RL) problem that we will refer to as return-conditioned supervised learning (RCSL). RCSL algorithms learn the distribution of actions conditioned on both the state and the return of the trajectory. Then they define a policy by conditioning on achieving high return. In this paper, we provide a rigorous study of the capabilities and limitations of RCSL, something which is crucially missing in previous work. We find that RCSL returns the optimal policy under a set of assumptions that are stronger than those needed for the more traditional dynamic programming-based algorithms. We provide specific examples of MDPs and datasets that illustrate the necessity of these assumptions and the limits of RCSL. Finally, we present empirical evidence that these limitations will also cause issues in practice by providing illustrative experiments in simple point-mass environments and on datasets from the D4RL benchmark.

Non-Markovian policies occupancy measures

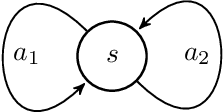
A central object of study in Reinforcement Learning (RL) is the Markovian policy, in which an agent's actions are chosen from a memoryless probability distribution, conditioned only on its current state. The family of Markovian policies is broad enough to be interesting, yet simple enough to be amenable to analysis. However, RL often involves more complex policies: ensembles of policies, policies over options, policies updated online, etc. Our main contribution is to prove that the occupancy measure of any non-Markovian policy, i.e., the distribution of transition samples collected with it, can be equivalently generated by a Markovian policy. This result allows theorems about the Markovian policy class to be directly extended to its non-Markovian counterpart, greatly simplifying proofs, in particular those involving replay buffers and datasets. We provide various examples of such applications to the field of Reinforcement Learning.

The Importance of Pessimism in Fixed-Dataset Policy Optimization

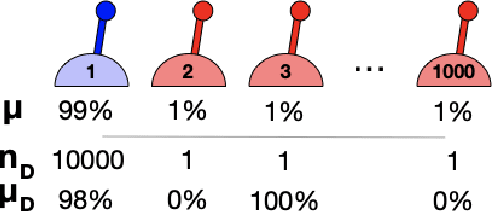
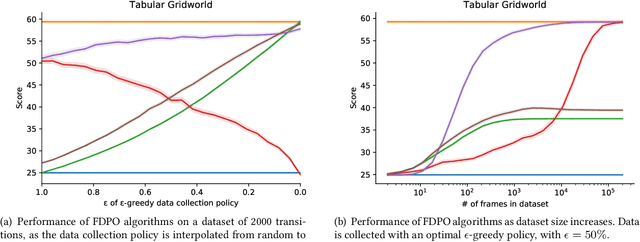
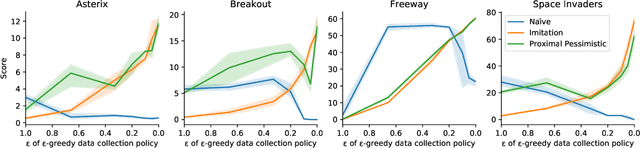
We study worst-case guarantees on the expected return of fixed-dataset policy optimization algorithms. Our core contribution is a unified conceptual and mathematical framework for the study of algorithms in this regime. This analysis reveals that for naive approaches, the possibility of erroneous value overestimation leads to a difficult-to-satisfy requirement: in order to guarantee that we select a policy which is near-optimal, we may need the dataset to be informative of the value of every policy. To avoid this, algorithms can follow the pessimism principle, which states that we should choose the policy which acts optimally in the worst possible world. We show why pessimistic algorithms can achieve good performance even when the dataset is not informative of every policy, and derive families of algorithms which follow this principle. These theoretical findings are validated by experiments on a tabular gridworld, and deep learning experiments on four MinAtar environments.

DeepMDP: Learning Continuous Latent Space Models for Representation Learning

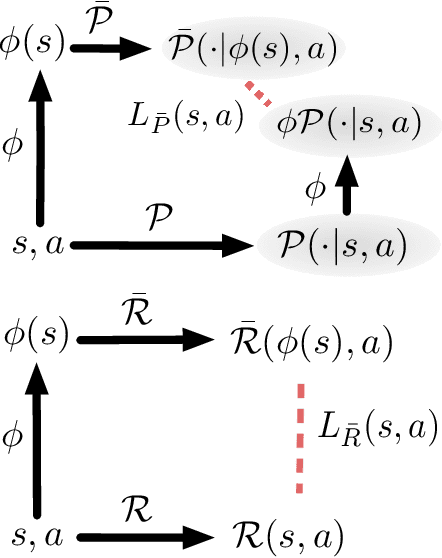
Many reinforcement learning (RL) tasks provide the agent with high-dimensional observations that can be simplified into low-dimensional continuous states. To formalize this process, we introduce the concept of a DeepMDP, a parameterized latent space model that is trained via the minimization of two tractable losses: prediction of rewards and prediction of the distribution over next latent states. We show that the optimization of these objectives guarantees (1) the quality of the latent space as a representation of the state space and (2) the quality of the DeepMDP as a model of the environment. We connect these results to prior work in the bisimulation literature, and explore the use of a variety of metrics. Our theoretical findings are substantiated by the experimental result that a trained DeepMDP recovers the latent structure underlying high-dimensional observations on a synthetic environment. Finally, we show that learning a DeepMDP as an auxiliary task in the Atari 2600 domain leads to large performance improvements over model-free RL.

Sample-Efficient Reinforcement Learning with Stochastic Ensemble Value Expansion

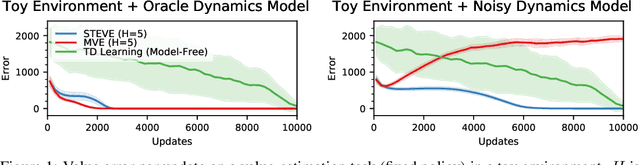
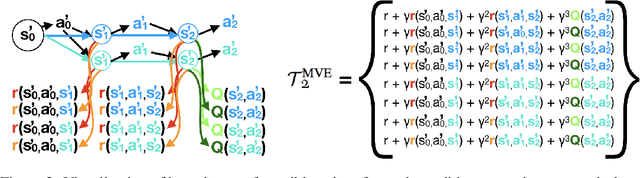
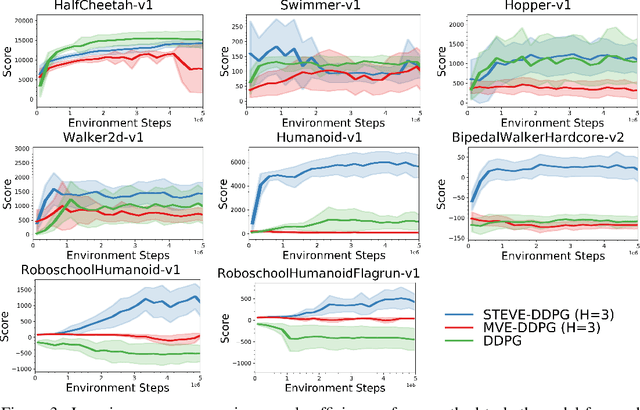
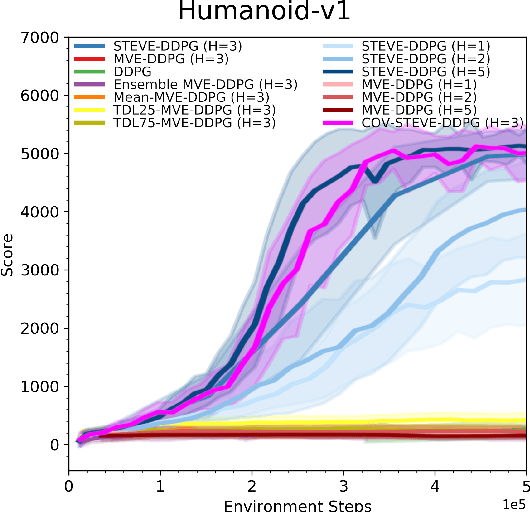
Integrating model-free and model-based approaches in reinforcement learning has the potential to achieve the high performance of model-free algorithms with low sample complexity. However, this is difficult because an imperfect dynamics model can degrade the performance of the learning algorithm, and in sufficiently complex environments, the dynamics model will almost always be imperfect. As a result, a key challenge is to combine model-based approaches with model-free learning in such a way that errors in the model do not degrade performance. We propose stochastic ensemble value expansion (STEVE), a novel model-based technique that addresses this issue. By dynamically interpolating between model rollouts of various horizon lengths for each individual example, STEVE ensures that the model is only utilized when doing so does not introduce significant errors. Our approach outperforms model-free baselines on challenging continuous control benchmarks with an order-of-magnitude increase in sample efficiency, and in contrast to previous model-based approaches, performance does not degrade in complex environments.

Is Generator Conditioning Causally Related to GAN Performance?

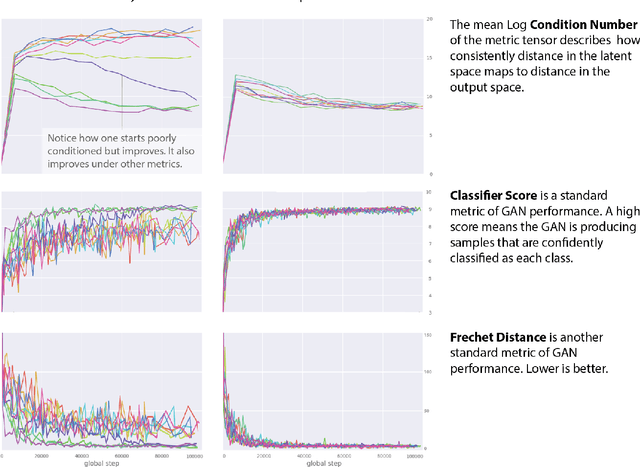
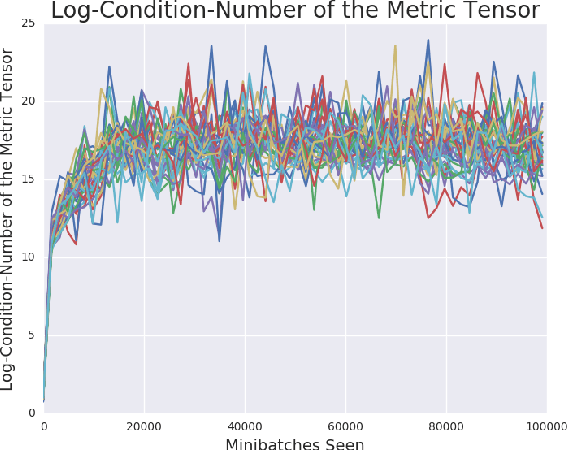
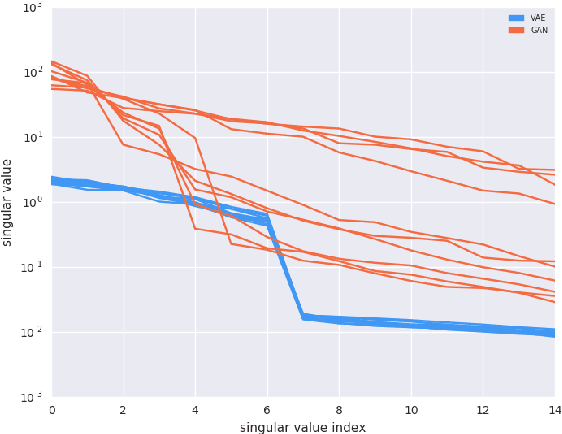
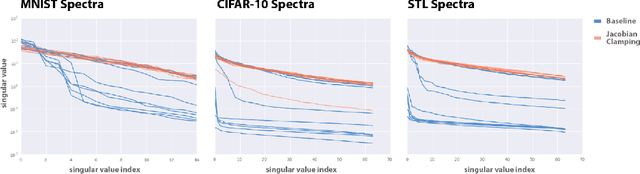
Recent work (Pennington et al, 2017) suggests that controlling the entire distribution of Jacobian singular values is an important design consideration in deep learning. Motivated by this, we study the distribution of singular values of the Jacobian of the generator in Generative Adversarial Networks (GANs). We find that this Jacobian generally becomes ill-conditioned at the beginning of training. Moreover, we find that the average (with z from p(z)) conditioning of the generator is highly predictive of two other ad-hoc metrics for measuring the 'quality' of trained GANs: the Inception Score and the Frechet Inception Distance (FID). We test the hypothesis that this relationship is causal by proposing a 'regularization' technique (called Jacobian Clamping) that softly penalizes the condition number of the generator Jacobian. Jacobian Clamping improves the mean Inception Score and the mean FID for GANs trained on several datasets. It also greatly reduces inter-run variance of the aforementioned scores, addressing (at least partially) one of the main criticisms of GANs.

Neural Lattice Language Models

In this work, we propose a new language modeling paradigm that has the ability to perform both prediction and moderation of information flow at multiple granularities: neural lattice language models. These models construct a lattice of possible paths through a sentence and marginalize across this lattice to calculate sequence probabilities or optimize parameters. This approach allows us to seamlessly incorporate linguistic intuitions - including polysemy and existence of multi-word lexical items - into our language model. Experiments on multiple language modeling tasks show that English neural lattice language models that utilize polysemous embeddings are able to improve perplexity by 9.95% relative to a word-level baseline, and that a Chinese model that handles multi-character tokens is able to improve perplexity by 20.94% relative to a character-level baseline.