DeepMDP: Learning Continuous Latent Space Models for Representation Learning
Paper and Code
Jun 06, 2019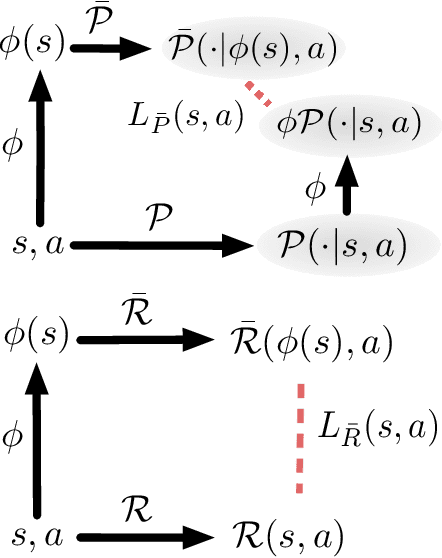


Many reinforcement learning (RL) tasks provide the agent with high-dimensional observations that can be simplified into low-dimensional continuous states. To formalize this process, we introduce the concept of a DeepMDP, a parameterized latent space model that is trained via the minimization of two tractable losses: prediction of rewards and prediction of the distribution over next latent states. We show that the optimization of these objectives guarantees (1) the quality of the latent space as a representation of the state space and (2) the quality of the DeepMDP as a model of the environment. We connect these results to prior work in the bisimulation literature, and explore the use of a variety of metrics. Our theoretical findings are substantiated by the experimental result that a trained DeepMDP recovers the latent structure underlying high-dimensional observations on a synthetic environment. Finally, we show that learning a DeepMDP as an auxiliary task in the Atari 2600 domain leads to large performance improvements over model-free RL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge