Is Generator Conditioning Causally Related to GAN Performance?
Paper and Code
Jun 19, 2018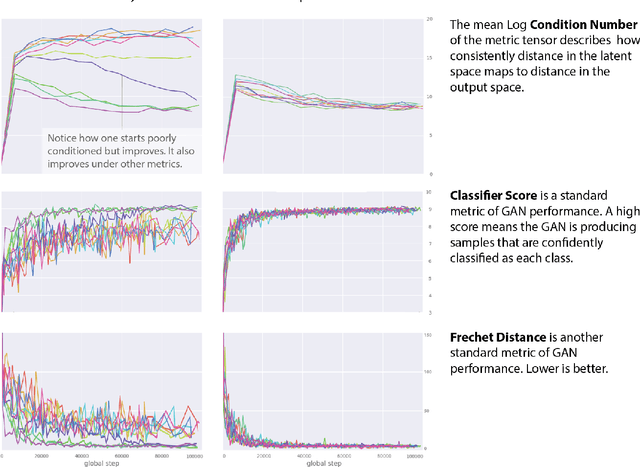
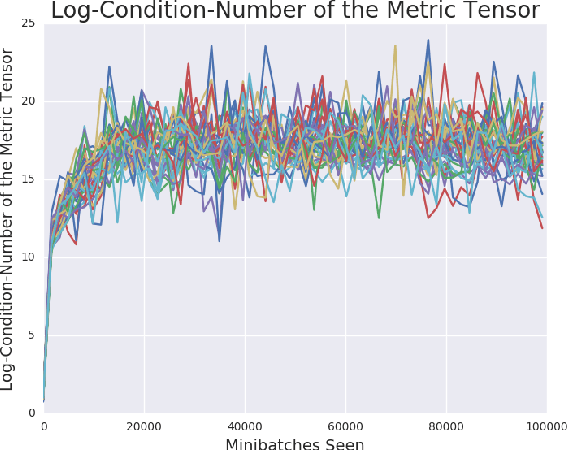
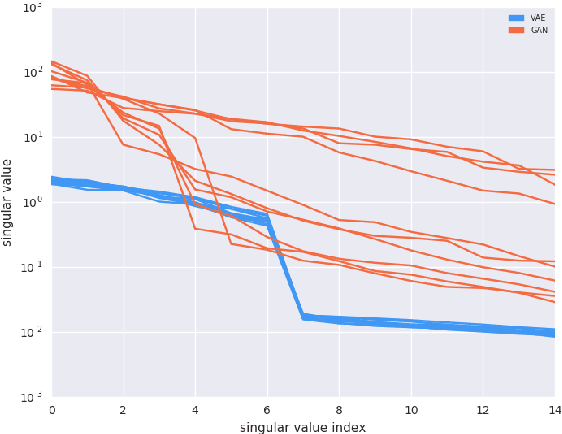
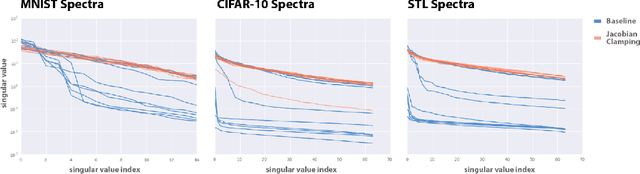
Recent work (Pennington et al, 2017) suggests that controlling the entire distribution of Jacobian singular values is an important design consideration in deep learning. Motivated by this, we study the distribution of singular values of the Jacobian of the generator in Generative Adversarial Networks (GANs). We find that this Jacobian generally becomes ill-conditioned at the beginning of training. Moreover, we find that the average (with z from p(z)) conditioning of the generator is highly predictive of two other ad-hoc metrics for measuring the 'quality' of trained GANs: the Inception Score and the Frechet Inception Distance (FID). We test the hypothesis that this relationship is causal by proposing a 'regularization' technique (called Jacobian Clamping) that softly penalizes the condition number of the generator Jacobian. Jacobian Clamping improves the mean Inception Score and the mean FID for GANs trained on several datasets. It also greatly reduces inter-run variance of the aforementioned scores, addressing (at least partially) one of the main criticisms of GANs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge